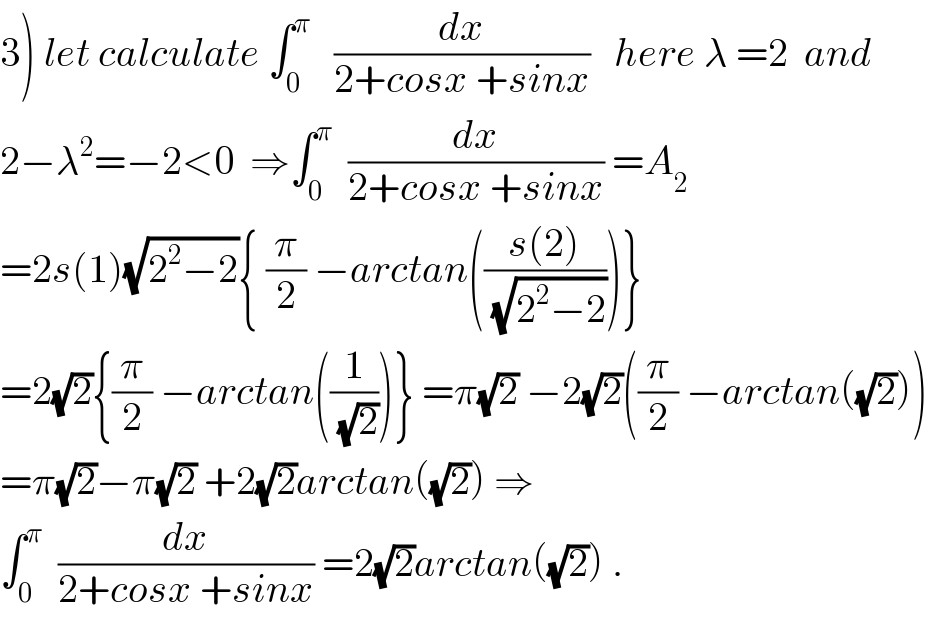Question Number 64850 by mathmax by abdo last updated on 22/Jul/19
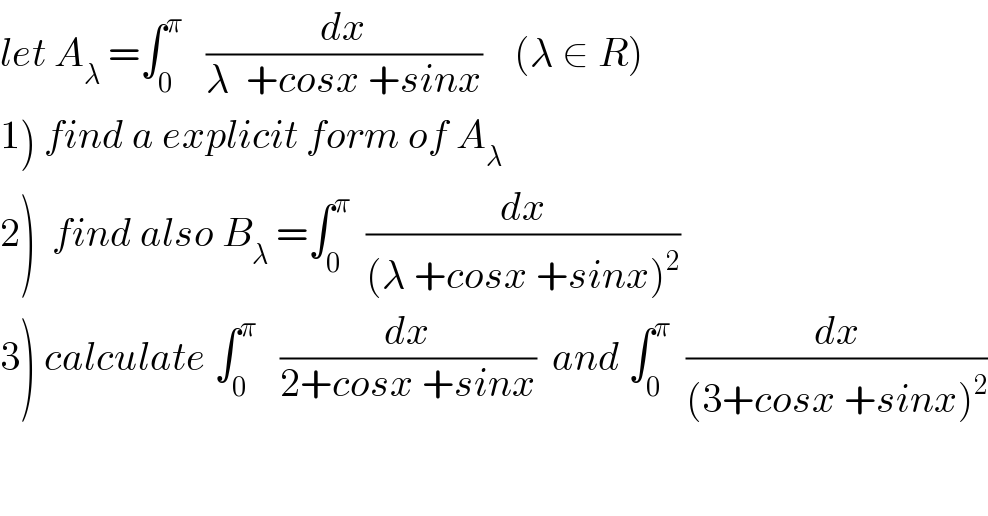
Commented by mathmax by abdo last updated on 23/Jul/19
![1) A_λ =∫_0 ^π (dx/(λ +cosx +sinx)) changement tan((x/2))=t give A_λ =∫_0 ^∞ (1/(λ +((1−t^2 )/(1+t^2 )) +((2t)/(1+t^2 )))) ((2dt)/(1+t^2 )) =∫_0 ^∞ ((2dt)/(λ+λt^2 +1−t^2 +2t)) =2∫_0 ^∞ (dt/((λ−1)t^2 +2t +1+λ)) let decompose F(t)=(1/((λ−1)t^2 +2t+1+λ)) Δ^′ =1−(λ−1)(λ+1) =1−(λ^2 −1) =2−λ^2 case 1 2−λ^2 >0 ⇒∣λ∣<(√2) ⇒t_1 =((−1+(√(2−λ^2 )))/(λ−1)) (λ≠1) t_2 =((−1−(√(2−λ^2 )))/(λ−1)) ⇒F(t) =(1/((λ−1)(t−t_1 )(t−t_2 ))) ⇒ A_λ =(2/(λ−1))∫_0 ^∞ (1/((2(√(2−λ^2 )))/(λ−1))) ((1/(t−t_1 )) −(1/(t−t_2 )))dt =(1/( (√(2−λ^2 ))))∫_0 ^∞ ((1/(t−t_1 ))−(1/(t−t_2 )))dt =(1/(2(√(2−λ^2 ))))[ln∣((t−t_1 )/(t−t_2 ))∣]_0 ^(+∞) =(1/(2(√(2−λ^2 ))))ln∣(t_2 /t_1 )∣ A_λ =(1/(2(√(2−λ^2 ))))ln∣((1+(√(2−λ^2 )))/(1−(√(2−λ^2 ))))∣](https://www.tinkutara.com/question/Q64995.png)
Commented by mathmax by abdo last updated on 23/Jul/19
![case 2 2−λ^2 <0 ⇒∣λ∣>(√2) ⇒Δ^′ <0 and (λ−1)t^2 +2t +1+λ =(λ−1){t^2 +(2/(λ−1))t +((1+λ)/(λ−1))} =(λ−1){ t^2 +((2t)/(λ−1)) +(1/((λ−1)^2 )) +((1+λ)/(λ−1)) −(1/((λ−1)^2 ))} =(λ−1){ (t +(1/(λ−1)))^2 +((λ^2 −2)/((λ−1)^2 ))} we use the changement t+(1/(λ−1)) =((√(λ^2 −2))/(∣λ−1∣)) u ⇒A_λ =(2/(λ−1))∫_0 ^∞ (dt/((t+(1/(λ−1)))^2 +((λ^2 −2)/((λ−1)^2 )))) =(2/(λ−1))∫_((s(λ))/( (√(λ^2 −2)))) ^(+∞) (1/(((λ^2 −2)/((λ−1)^2 ))(1+u^2 )))((√(λ^2 −2))/(∣λ−1∣)) du =((2(λ−1)^2 )/((λ−1)∣λ−1∣)) (√(λ^2 −2)) [arctanu]_((s(λ))/( (√(λ^2 −2)))) ^(+∞) A_λ =2s(λ−1)(√(λ^2 −2)) ((π/2) −arctan(((s(λ))/( (√(λ^2 −2)))))) with s(x) =1 if x>0 and s(x)=−1 if x<0](https://www.tinkutara.com/question/Q64996.png)
Commented by mathmax by abdo last updated on 23/Jul/19
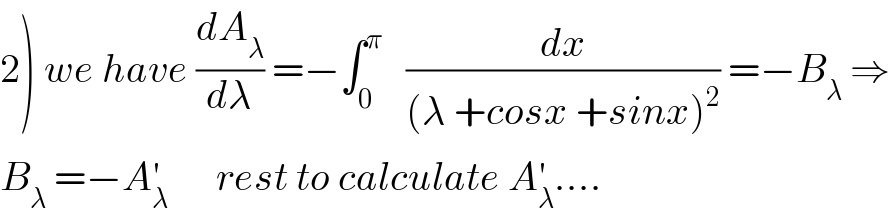
Commented by mathmax by abdo last updated on 23/Jul/19