Question Number 102576 by MAB last updated on 10/Jul/20

Answered by mr W last updated on 10/Jul/20
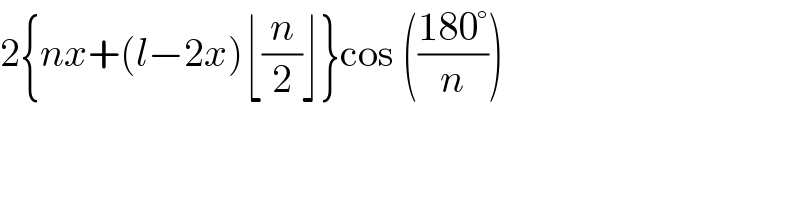
Commented by MAB last updated on 10/Jul/20
Commented by mr W last updated on 10/Jul/20

Commented by MAB last updated on 10/Jul/20
Answered by mr W last updated on 10/Jul/20

Commented by mr W last updated on 10/Jul/20

Commented by mr W last updated on 10/Jul/20

Commented by mr W last updated on 10/Jul/20
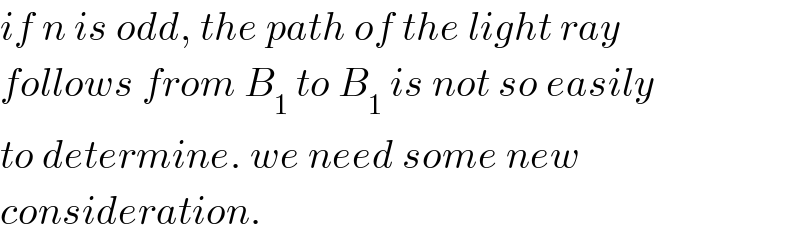
Commented by MAB last updated on 10/Jul/20

Commented by mr W last updated on 10/Jul/20

Commented by mr W last updated on 10/Jul/20

