Menu Close

let-A-2-1-1-2-1-calculate-A-n-2-determine-cosA-and-sinA-3-find-chA-and-shA-

Tinku Tara 0 Comments
Pin




Question Number 99828 by mathmax by abdo last updated on 23/Jun/20
let A = (((2 1)),((1 2)) ) 1) calculate A^n 2)determine cosA and sinA 3) find chA and shA
$$\mathrm{let}\:\mathrm{A}\:=\begin{pmatrix}{\mathrm{2}\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}}\\{\mathrm{1}\:\:\:\:\:\:\mathrm{2}}\end{pmatrix} \\ $$$$\left.\mathrm{1}\right)\:\mathrm{calculate}\:\mathrm{A}^{\mathrm{n}} \\ $$$$\left.\mathrm{2}\right)\mathrm{determine}\:\mathrm{cosA}\:\mathrm{and}\:\mathrm{sinA} \\ $$$$\left.\mathrm{3}\right)\:\mathrm{find}\:\mathrm{chA}\:\mathrm{and}\:\mathrm{shA} \\ $$
Commented by bachamohamed last updated on 23/Jun/20
1) A= (((2 1)),((1 2)) ) p_A (𝛌)=det(A−𝛌I_2 )=(𝛌−1)(𝛌−2) donc les valeurs propres sont {_(𝛌_2 =2) ^(𝛌_1 =1) E_𝛌_1 =<(−1.1)> E_𝛌_2 =<(1.1)> ou les vecteurs propres sont {_(v_2 =(1.1)) ^(v_1 =(−1.1)) et donc ∃ p ∈M_(2x2) (R) telle que B=p^(−1) A.p on a id_E (R^2 .(v_1 .v_2 ))→^(p matrix de id_E ) (R^2 .(e_1 .e_2 )) en deduire que p= (((−1 1)),(( 1 1)) ) et p^(−1) = (((−(1/2) (1/2))),(( (1/2) (1/2))) ) B=p^(−1) Ap = (((1 0)),((0 3)) ) et B^n =(p^(−1) Ap)^n =(p^(−1) Ap)(p^(−1) Ap)......^(n fois) ......(p^(−1) Ap)=p^(−1) A^n .p ⇒ A^n =p.B^n .p^(−1) ⇒A^n =(1/2) ((((3^n +1) 3^n −1)),((3^n −1 3^n +1)) )
$$\left.\:\:\:\:\mathrm{1}\right)\:\: \\ $$$$\boldsymbol{{A}}=\begin{pmatrix}{\mathrm{2}\:\:\:\mathrm{1}}\\{\mathrm{1}\:\:\:\:\mathrm{2}}\end{pmatrix}\:\: \\ $$$$\boldsymbol{{p}}_{\boldsymbol{{A}}} \left(\boldsymbol{\lambda}\right)=\boldsymbol{{det}}\left(\boldsymbol{{A}}−\boldsymbol{\lambda{I}}_{\mathrm{2}} \right)=\left(\boldsymbol{\lambda}−\mathrm{1}\right)\left(\boldsymbol{\lambda}−\mathrm{2}\right)\:\:\:\boldsymbol{{donc}}\:\:\boldsymbol{{les}}\:\boldsymbol{{valeurs}}\:\boldsymbol{{propres}}\:\boldsymbol{{sont}}\:\:\left\{_{\boldsymbol{\lambda}_{\mathrm{2}} =\mathrm{2}} ^{\boldsymbol{\lambda}_{\mathrm{1}} =\mathrm{1}} \right. \\ $$$$\boldsymbol{{E}}_{\boldsymbol{\lambda}_{\mathrm{1}} } =<\left(−\mathrm{1}.\mathrm{1}\right)>\:\:\:\:\:\:\boldsymbol{{E}}_{\boldsymbol{\lambda}_{\mathrm{2}} } =<\left(\mathrm{1}.\mathrm{1}\right)>\:\:\:\:\boldsymbol{{ou}}\:\:\:\boldsymbol{{les}}\:\boldsymbol{{vecteurs}}\:\boldsymbol{{propres}}\:\boldsymbol{{sont}}\:\left\{_{\boldsymbol{{v}}_{\mathrm{2}} =\left(\mathrm{1}.\mathrm{1}\right)} ^{\boldsymbol{{v}}_{\mathrm{1}} =\left(−\mathrm{1}.\mathrm{1}\right)} \right. \\ $$$$\boldsymbol{{et}}\:\:\boldsymbol{{donc}}\:\:\exists\:\boldsymbol{{p}}\:\in\boldsymbol{{M}}_{\mathrm{2×2}} \left(\mathrm{R}\right)\:\:\:\:\boldsymbol{{telle}}\:\boldsymbol{{que}}\:\:\boldsymbol{{B}}=\boldsymbol{{p}}^{−\mathrm{1}} \boldsymbol{{A}}.\boldsymbol{{p}} \\ $$$$\boldsymbol{{on}}\:\boldsymbol{{a}}\:\:\boldsymbol{{id}}_{\boldsymbol{{E}}} \:\:\left(\boldsymbol{{R}}^{\mathrm{2}} .\left(\boldsymbol{{v}}_{\mathrm{1}} .\boldsymbol{{v}}_{\mathrm{2}} \right)\right)\overset{\boldsymbol{{p}}\:\:\boldsymbol{{matrix}}\:\boldsymbol{{de}}\:\boldsymbol{{id}}_{\boldsymbol{{E}}} } {\rightarrow}\left(\boldsymbol{{R}}^{\mathrm{2}} .\left(\boldsymbol{{e}}_{\mathrm{1}} .\boldsymbol{{e}}_{\mathrm{2}} \right)\right)\:\:\:\boldsymbol{{en}}\:\boldsymbol{{deduire}}\:\boldsymbol{{que}}\:\:\boldsymbol{{p}}=\begin{pmatrix}{−\mathrm{1}\:\:\:\:\:\mathrm{1}}\\{\:\:\mathrm{1}\:\:\:\:\:\:\mathrm{1}}\end{pmatrix}\:\:\:\:\boldsymbol{{et}}\:\:\:\boldsymbol{{p}}^{−\mathrm{1}} =\begin{pmatrix}{−\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}}\\{\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}}\end{pmatrix}\:\:\: \\ $$$$\boldsymbol{{B}}=\boldsymbol{{p}}^{−\mathrm{1}} \boldsymbol{{Ap}}\:=\begin{pmatrix}{\mathrm{1}\:\:\mathrm{0}}\\{\mathrm{0}\:\:\:\mathrm{3}}\end{pmatrix}\:\:\:\:\boldsymbol{{et}}\:\boldsymbol{{B}}^{\boldsymbol{{n}}} =\left(\boldsymbol{{p}}^{−\mathrm{1}} \boldsymbol{{Ap}}\right)^{\boldsymbol{{n}}} =\left(\boldsymbol{{p}}^{−\mathrm{1}} \boldsymbol{{Ap}}\right)\left(\boldsymbol{{p}}^{−\mathrm{1}} \boldsymbol{{Ap}}\right)…..\overset{\boldsymbol{{n}}\:\boldsymbol{{fois}}} {.}……\left(\boldsymbol{{p}}^{−\mathrm{1}} \boldsymbol{{Ap}}\right)=\boldsymbol{{p}}^{−\mathrm{1}} \boldsymbol{{A}}^{\boldsymbol{{n}}} .\boldsymbol{{p}}\:\:\:\:\:\Rightarrow\:\:\boldsymbol{{A}}^{\boldsymbol{{n}}} =\boldsymbol{{p}}.\boldsymbol{{B}}^{\boldsymbol{{n}}} .\boldsymbol{{p}}^{−\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\boldsymbol{{A}}^{\boldsymbol{{n}}} =\frac{\mathrm{1}}{\mathrm{2}}\begin{pmatrix}{\left(\mathrm{3}^{\boldsymbol{{n}}} +\mathrm{1}\right)\:\:\:\:\:\:\:\mathrm{3}^{\boldsymbol{{n}}} −\mathrm{1}}\\{\mathrm{3}^{\boldsymbol{{n}}} −\mathrm{1}\:\:\:\:\:\:\:\:\:\:\mathrm{3}^{\boldsymbol{{n}}} +\mathrm{1}}\end{pmatrix} \\ $$
Commented by mathmax by abdo last updated on 23/Jun/20
thankx sir.
$$\mathrm{thankx}\:\mathrm{sir}. \\ $$
Answered by mathmax by abdo last updated on 23/Jun/20
1) the caracteristic polynome is P_c (A) =det(A−xI)= determinant (((2−x 1)),((1 2−x))) =(2−x)^2 −1 =(x−2)^2 −1 =(x−2−1)(x−2+1) =(x−3)(x−1) ⇒ ⇒λ_1 =1 and λ_2 =3 we have x^(n ) =p_c (x)q +u_n x+v_n ⇒ 1 =u_n +v_n and 3^n =3u_n +v_n ⇒2u_n =3^n −1 ⇒u_n =((3^n −1)/2) v_n =1−u_n =1−((3^n −1)/2) =((2−3^n +1)/2) =((3−3^n )/2) we have A^n =u_n A +v_n I=((3^n −1)/2) (((2 1)),((1 2)) ) +((3−3^n )/2) (((1 0)),((0 1)) ) = (((3^n −1 ((3^n −1)/2))),((((3^n −1)/2) 3^n −1)) ) + (((((3−3^n )/2) 0)),((0 ((3−3^n )/2))) ) = (((((2.3^n −2+3−3^n )/2) ((3^n −1)/2))),((((3^n −1)/2) ((2.3^n −2+3−3^n )/2))) ) = (((((3^n +1)/2) ((3^n −1)/2))),((((3^n −1)/2) ((3^n +1)/2))) )
$$\left.\mathrm{1}\right)\:\mathrm{the}\:\mathrm{caracteristic}\:\mathrm{polynome}\:\mathrm{is}\:\mathrm{P}_{\mathrm{c}} \left(\mathrm{A}\right)\:=\mathrm{det}\left(\mathrm{A}−\mathrm{xI}\right)=\begin{vmatrix}{\mathrm{2}−\mathrm{x}\:\:\:\:\:\:\:\:\mathrm{1}}\\{\mathrm{1}\:\:\:\:\:\:\:\:\:\:\mathrm{2}−\mathrm{x}}\end{vmatrix} \\ $$$$=\left(\mathrm{2}−\mathrm{x}\right)^{\mathrm{2}} −\mathrm{1}\:=\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} −\mathrm{1}\:=\left(\mathrm{x}−\mathrm{2}−\mathrm{1}\right)\left(\mathrm{x}−\mathrm{2}+\mathrm{1}\right)\:=\left(\mathrm{x}−\mathrm{3}\right)\left(\mathrm{x}−\mathrm{1}\right)\:\Rightarrow \\ $$$$\Rightarrow\lambda_{\mathrm{1}} =\mathrm{1}\:\mathrm{and}\:\lambda_{\mathrm{2}} =\mathrm{3}\:\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{x}^{\mathrm{n}\:} \:=\mathrm{p}_{\mathrm{c}} \left(\mathrm{x}\right)\mathrm{q}\:+\mathrm{u}_{\mathrm{n}} \mathrm{x}+\mathrm{v}_{\mathrm{n}} \:\Rightarrow \\ $$$$\mathrm{1}\:=\mathrm{u}_{\mathrm{n}} \:+\mathrm{v}_{\mathrm{n}} \:\mathrm{and}\:\mathrm{3}^{\mathrm{n}} \:=\mathrm{3u}_{\mathrm{n}} \:+\mathrm{v}_{\mathrm{n}} \:\Rightarrow\mathrm{2u}_{\mathrm{n}} =\mathrm{3}^{\mathrm{n}} −\mathrm{1}\:\Rightarrow\mathrm{u}_{\mathrm{n}} =\frac{\mathrm{3}^{\mathrm{n}} −\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{v}_{\mathrm{n}} =\mathrm{1}−\mathrm{u}_{\mathrm{n}} =\mathrm{1}−\frac{\mathrm{3}^{\mathrm{n}} −\mathrm{1}}{\mathrm{2}}\:=\frac{\mathrm{2}−\mathrm{3}^{\mathrm{n}} +\mathrm{1}}{\mathrm{2}}\:=\frac{\mathrm{3}−\mathrm{3}^{\mathrm{n}} }{\mathrm{2}} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{A}^{\mathrm{n}} \:=\mathrm{u}_{\mathrm{n}} \:\mathrm{A}\:+\mathrm{v}_{\mathrm{n}} \mathrm{I}=\frac{\mathrm{3}^{\mathrm{n}} −\mathrm{1}}{\mathrm{2}}\:\begin{pmatrix}{\mathrm{2}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}}\\{\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}}\end{pmatrix}\:\:+\frac{\mathrm{3}−\mathrm{3}^{\mathrm{n}} }{\mathrm{2}}\begin{pmatrix}{\mathrm{1}\:\:\:\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix} \\ $$$$=\begin{pmatrix}{\mathrm{3}^{\mathrm{n}} −\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{3}^{\mathrm{n}} −\mathrm{1}}{\mathrm{2}}}\\{\frac{\mathrm{3}^{\mathrm{n}} −\mathrm{1}}{\mathrm{2}}\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3}^{\mathrm{n}} −\mathrm{1}}\end{pmatrix}\:+\begin{pmatrix}{\frac{\mathrm{3}−\mathrm{3}^{\mathrm{n}} }{\mathrm{2}}\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{3}−\mathrm{3}^{\mathrm{n}} }{\mathrm{2}}}\end{pmatrix} \\ $$$$=\begin{pmatrix}{\frac{\mathrm{2}.\mathrm{3}^{\mathrm{n}} −\mathrm{2}+\mathrm{3}−\mathrm{3}^{\mathrm{n}} }{\mathrm{2}}\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{3}^{\mathrm{n}} −\mathrm{1}}{\mathrm{2}}}\\{\frac{\mathrm{3}^{\mathrm{n}} −\mathrm{1}}{\mathrm{2}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{2}.\mathrm{3}^{\mathrm{n}} −\mathrm{2}+\mathrm{3}−\mathrm{3}^{\mathrm{n}} }{\mathrm{2}}}\end{pmatrix} \\ $$$$=\begin{pmatrix}{\frac{\mathrm{3}^{\mathrm{n}} \:+\mathrm{1}}{\mathrm{2}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{3}^{\mathrm{n}} −\mathrm{1}}{\mathrm{2}}}\\{\frac{\mathrm{3}^{\mathrm{n}} −\mathrm{1}}{\mathrm{2}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{3}^{\mathrm{n}} +\mathrm{1}}{\mathrm{2}}}\end{pmatrix} \\ $$
Commented by mathmax by abdo last updated on 24/Jun/20
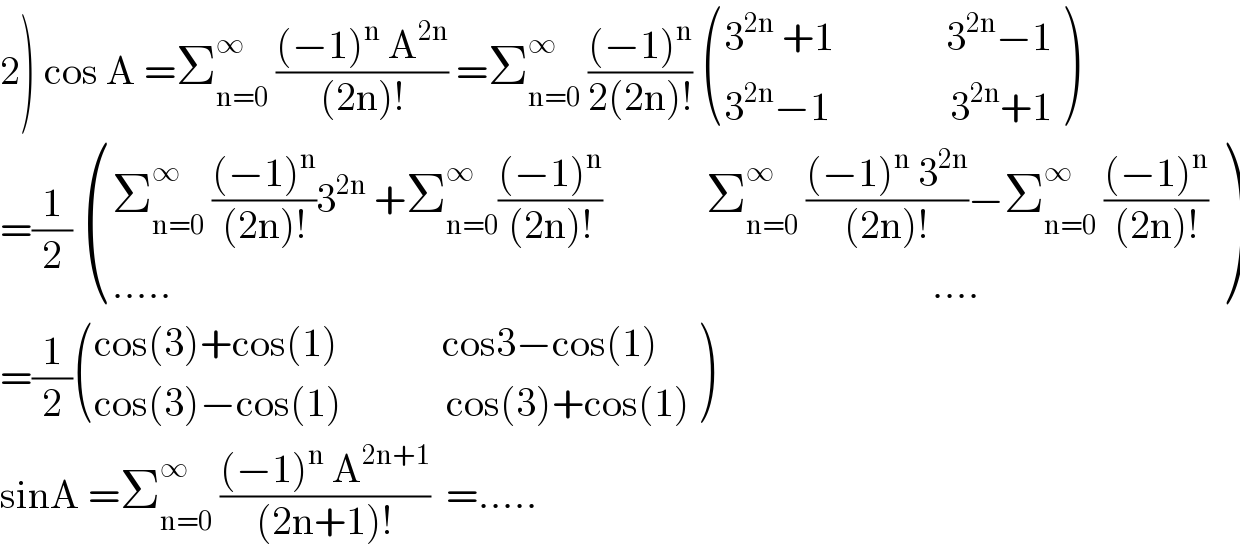
2) cos A =Σ_(n=0) ^∞ (((−1)^n A^(2n) )/((2n)!)) =Σ_(n=0) ^∞ (((−1)^n )/(2(2n)!)) (((3^(2n) +1 3^(2n) −1)),((3^(2n) −1 3^(2n) +1)) ) =(1/2) (((Σ_(n=0) ^∞ (((−1)^n )/((2n)!))3^(2n) +Σ_(n=0) ^∞ (((−1)^n )/((2n)!)) Σ_(n=0) ^∞ (((−1)^n 3^(2n) )/((2n)!))−Σ_(n=0) ^∞ (((−1)^n )/((2n)!)))),((..... ....)) ) =(1/2) (((cos(3)+cos(1) cos3−cos(1))),((cos(3)−cos(1) cos(3)+cos(1))) ) sinA =Σ_(n=0) ^∞ (((−1)^n A^(2n+1) )/((2n+1)!)) =.....
$$\left.\mathrm{2}\right)\:\mathrm{cos}\:\mathrm{A}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{A}^{\mathrm{2n}} }{\left(\mathrm{2n}\right)!}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{2}\left(\mathrm{2n}\right)!}\:\begin{pmatrix}{\mathrm{3}^{\mathrm{2n}} \:+\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3}^{\mathrm{2n}} −\mathrm{1}}\\{\mathrm{3}^{\mathrm{2n}} −\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3}^{\mathrm{2n}} +\mathrm{1}}\end{pmatrix} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\begin{pmatrix}{\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}\right)!}\mathrm{3}^{\mathrm{2n}} \:+\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}\right)!}\:\:\:\:\:\:\:\:\:\:\:\:\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{3}^{\mathrm{2n}} }{\left(\mathrm{2n}\right)!}−\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}\right)!}}\\{…..\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:….}\end{pmatrix} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\begin{pmatrix}{\mathrm{cos}\left(\mathrm{3}\right)+\mathrm{cos}\left(\mathrm{1}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{cos3}−\mathrm{cos}\left(\mathrm{1}\right)}\\{\mathrm{cos}\left(\mathrm{3}\right)−\mathrm{cos}\left(\mathrm{1}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{cos}\left(\mathrm{3}\right)+\mathrm{cos}\left(\mathrm{1}\right)}\end{pmatrix} \\ $$$$\mathrm{sinA}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{A}^{\mathrm{2n}+\mathrm{1}} }{\left(\mathrm{2n}+\mathrm{1}\right)!}\:\:=….. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *