Menu Close

let-A-a-b-c-d-use-the-augmented-matrix-A-I-and-elementary-row-operation-to-show-A-1-1-ad-bc-a-b-c-d-and-show-that-det-A-1-1-det-A-

Tinku Tara 0 Comments
Pin




Question Number 78670 by berket last updated on 19/Jan/20
let A= [((a b)),((c d)) ]use the augmented matrix[A I] and elementary row operation to show A^(−1) = (1/(ad bc)) [((a b)),((c d)) ]and show that det(A^(−1) )=(1/(det(A)))
$${let}\:{A}=\begin{bmatrix}{{a}\:\:{b}}\\{{c}\:\:{d}}\end{bmatrix}{use}\:{the}\:{augmented}\:{matrix}\left[{A}\:{I}\right]\:{and}\:{elementary}\:{row}\:{operation}\:{to}\:{show}\:{A}^{−\mathrm{1}} =\:\frac{\mathrm{1}}{{ad}\:{bc}}\begin{bmatrix}{{a}\:\:{b}}\\{{c}\:\:\:{d}}\end{bmatrix}{and}\:{show}\:{that}\:{det}\left({A}^{−\mathrm{1}} \right)=\frac{\mathrm{1}}{{det}\left({A}\right)} \\ $$$$ \\ $$
Commented by abdomathmax last updated on 20/Jan/20
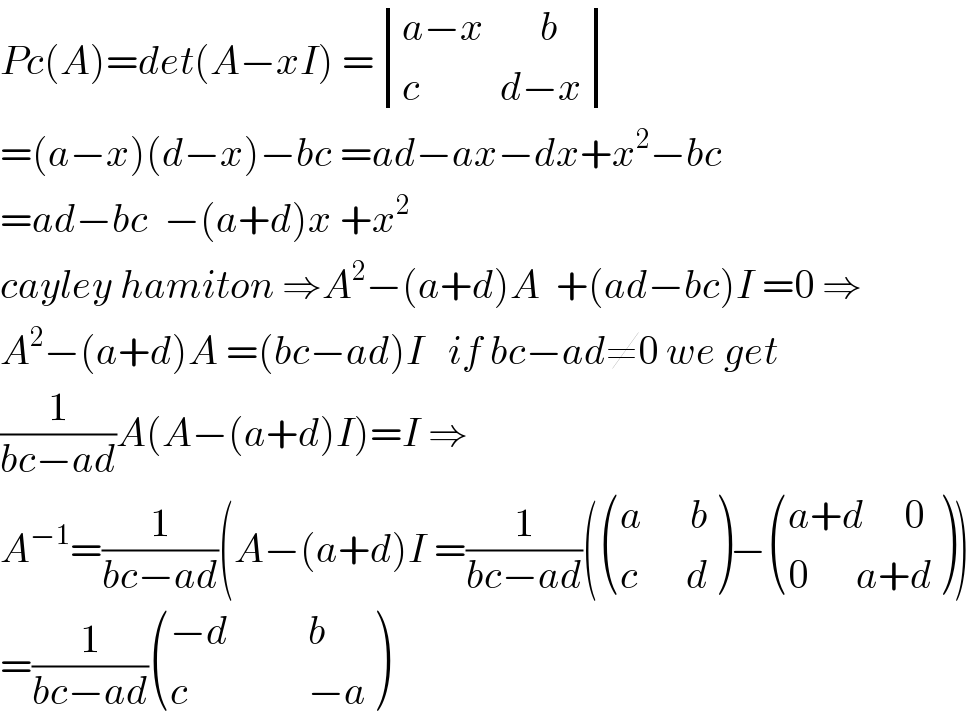
Pc(A)=det(A−xI) = determinant (((a−x b)),((c d−x))) =(a−x)(d−x)−bc =ad−ax−dx+x^2 −bc =ad−bc −(a+d)x +x^2 cayley hamiton ⇒A^2 −(a+d)A +(ad−bc)I =0 ⇒ A^2 −(a+d)A =(bc−ad)I if bc−ad≠0 we get (1/(bc−ad))A(A−(a+d)I)=I ⇒ A^(−1) =(1/(bc−ad))(A−(a+d)I =(1/(bc−ad))( (((a b)),((c d)) )− (((a+d 0)),((0 a+d)) )) =(1/(bc−ad)) (((−d b)),((c −a)) )
$${Pc}\left({A}\right)={det}\left({A}−{xI}\right)\:=\begin{vmatrix}{{a}−{x}\:\:\:\:\:\:\:{b}}\\{{c}\:\:\:\:\:\:\:\:\:\:{d}−{x}}\end{vmatrix} \\ $$$$=\left({a}−{x}\right)\left({d}−{x}\right)−{bc}\:={ad}−{ax}−{dx}+{x}^{\mathrm{2}} −{bc} \\ $$$$={ad}−{bc}\:\:−\left({a}+{d}\right){x}\:+{x}^{\mathrm{2}} \\ $$$${cayley}\:{hamiton}\:\Rightarrow{A}^{\mathrm{2}} −\left({a}+{d}\right){A}\:\:+\left({ad}−{bc}\right){I}\:=\mathrm{0}\:\Rightarrow \\ $$$${A}^{\mathrm{2}} −\left({a}+{d}\right){A}\:=\left({bc}−{ad}\right){I}\:\:\:{if}\:{bc}−{ad}\neq\mathrm{0}\:{we}\:{get} \\ $$$$\frac{\mathrm{1}}{{bc}−{ad}}{A}\left({A}−\left({a}+{d}\right){I}\right)={I}\:\Rightarrow \\ $$$${A}^{−\mathrm{1}} =\frac{\mathrm{1}}{{bc}−{ad}}\left({A}−\left({a}+{d}\right){I}\:=\frac{\mathrm{1}}{{bc}−{ad}}\left(\begin{pmatrix}{{a}\:\:\:\:\:\:{b}}\\{{c}\:\:\:\:\:\:{d}}\end{pmatrix}−\begin{pmatrix}{{a}+{d}\:\:\:\:\:\mathrm{0}}\\{\mathrm{0}\:\:\:\:\:\:{a}+{d}}\end{pmatrix}\right)\right. \\ $$$$=\frac{\mathrm{1}}{{bc}−{ad}}\begin{pmatrix}{−{d}\:\:\:\:\:\:\:\:\:\:{b}}\\{{c}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−{a}}\end{pmatrix} \\ $$
Commented by abdomathmax last updated on 20/Jan/20
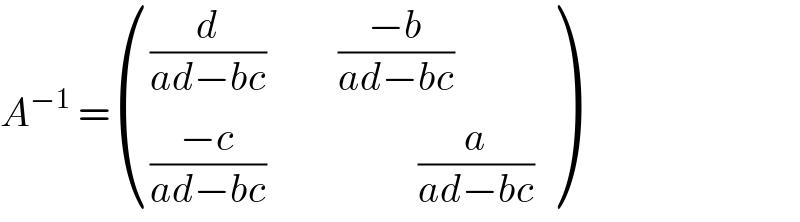
A^(−1) = ((((d/(ad−bc)) ((−b)/(ad−bc)))),((((−c)/(ad−bc)) (a/(ad−bc)))) )
$${A}^{−\mathrm{1}} \:=\begin{pmatrix}{\frac{{d}}{{ad}−{bc}}\:\:\:\:\:\:\:\:\:\frac{−{b}}{{ad}−{bc}}}\\{\frac{−{c}}{{ad}−{bc}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{{a}}{{ad}−{bc}}}\end{pmatrix} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *