Menu Close

Let-a-and-b-are-real-numbers-such-that-a-gt-b-gt-0-Find-the-minimum-value-of-2-a-3-3-ab-b-2-

Tinku Tara 0 Comments
Pin




Question Number 44384 by Joel578 last updated on 28/Sep/18
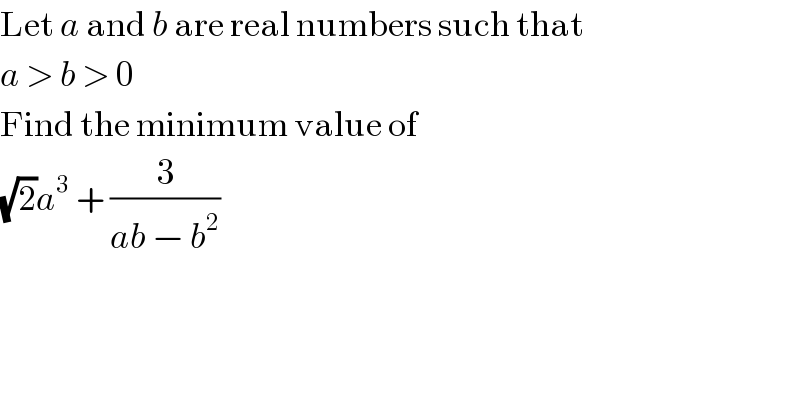
Let a and b are real numbers such that a > b > 0 Find the minimum value of (√2)a^3 + (3/(ab − b^2 ))
$$\mathrm{Let}\:{a}\:\mathrm{and}\:{b}\:\mathrm{are}\:\mathrm{real}\:\mathrm{numbers}\:\mathrm{such}\:\mathrm{that} \\ $$$${a}\:>\:{b}\:>\:\mathrm{0} \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{minimum}\:\mathrm{value}\:\mathrm{of} \\ $$$$\sqrt{\mathrm{2}}{a}^{\mathrm{3}} \:+\:\frac{\mathrm{3}}{{ab}\:−\:{b}^{\mathrm{2}} } \\ $$
Commented by behi83417@gmail.com last updated on 28/Sep/18
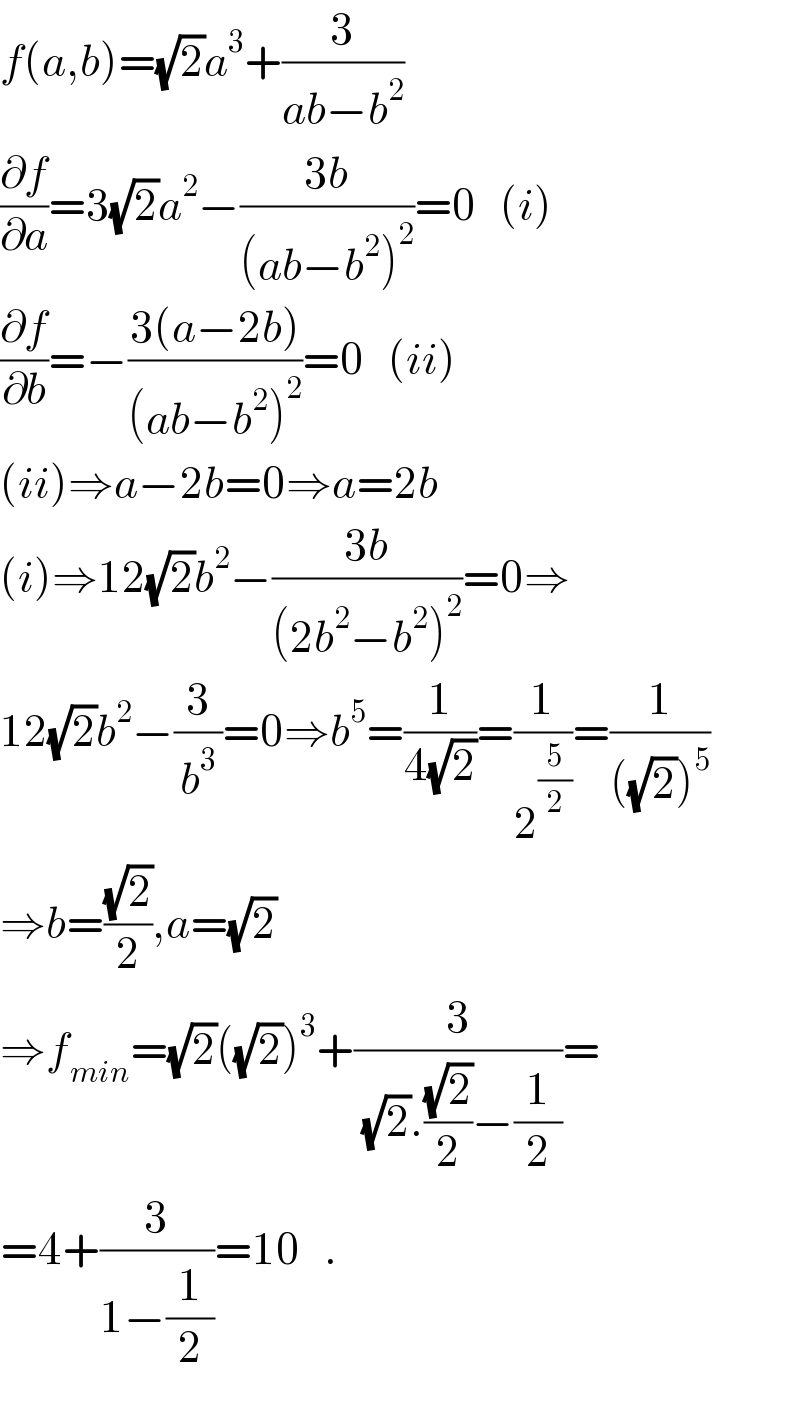
f(a,b)=(√2)a^3 +(3/(ab−b^2 )) (∂f/∂a)=3(√2)a^2 −((3b)/((ab−b^2 )^2 ))=0 (i) (∂f/∂b)=−((3(a−2b))/((ab−b^2 )^2 ))=0 (ii) (ii)⇒a−2b=0⇒a=2b (i)⇒12(√2)b^2 −((3b)/((2b^2 −b^2 )^2 ))=0⇒ 12(√2)b^2 −(3/b^3 )=0⇒b^5 =(1/(4(√2)))=(1/2^(5/2) )=(1/(((√2))^5 )) ⇒b=((√2)/2),a=(√2) ⇒f_(min) =(√2)((√2))^3 +(3/( (√2).((√2)/2)−(1/2)))= =4+(3/(1−(1/2)))=10 .
$${f}\left({a},{b}\right)=\sqrt{\mathrm{2}}{a}^{\mathrm{3}} +\frac{\mathrm{3}}{{ab}−{b}^{\mathrm{2}} } \\ $$$$\frac{\partial{f}}{\partial{a}}=\mathrm{3}\sqrt{\mathrm{2}}{a}^{\mathrm{2}} −\frac{\mathrm{3}{b}}{\left({ab}−{b}^{\mathrm{2}} \right)^{\mathrm{2}} }=\mathrm{0}\:\:\:\left({i}\right) \\ $$$$\frac{\partial{f}}{\partial{b}}=−\frac{\mathrm{3}\left({a}−\mathrm{2}{b}\right)}{\left({ab}−{b}^{\mathrm{2}} \right)^{\mathrm{2}} }=\mathrm{0}\:\:\:\left({ii}\right) \\ $$$$\left({ii}\right)\Rightarrow{a}−\mathrm{2}{b}=\mathrm{0}\Rightarrow{a}=\mathrm{2}{b} \\ $$$$\left({i}\right)\Rightarrow\mathrm{12}\sqrt{\mathrm{2}}{b}^{\mathrm{2}} −\frac{\mathrm{3}{b}}{\left(\mathrm{2}{b}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} }=\mathrm{0}\Rightarrow \\ $$$$\mathrm{12}\sqrt{\mathrm{2}}{b}^{\mathrm{2}} −\frac{\mathrm{3}}{{b}^{\mathrm{3}} }=\mathrm{0}\Rightarrow{b}^{\mathrm{5}} =\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}=\frac{\mathrm{1}}{\mathrm{2}^{\frac{\mathrm{5}}{\mathrm{2}}} }=\frac{\mathrm{1}}{\left(\sqrt{\mathrm{2}}\right)^{\mathrm{5}} } \\ $$$$\Rightarrow{b}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}},{a}=\sqrt{\mathrm{2}} \\ $$$$\Rightarrow{f}_{{min}} =\sqrt{\mathrm{2}}\left(\sqrt{\mathrm{2}}\right)^{\mathrm{3}} +\frac{\mathrm{3}}{\:\sqrt{\mathrm{2}}.\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}}= \\ $$$$=\mathrm{4}+\frac{\mathrm{3}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}}=\mathrm{10}\:\:\:. \\ $$
Commented by ajfour last updated on 28/Sep/18
Very grateful Sir!
$${Very}\:{grateful}\:{Sir}! \\ $$
Commented by rahul 19 last updated on 28/Sep/18
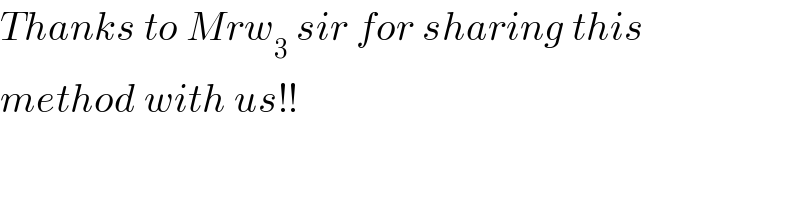
Thanks to Mrw_3 sir for sharing this method with us!!
$${Thanks}\:{to}\:{Mrw}_{\mathrm{3}} \:{sir}\:{for}\:{sharing}\:{this} \\ $$$${method}\:{with}\:{us}!! \\ $$
Commented by Joel578 last updated on 28/Sep/18
Thank you very much
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 28/Sep/18
Commented by tanmay.chaudhury50@gmail.com last updated on 28/Sep/18
Answered by ajfour last updated on 28/Sep/18
let x= (√2)a^3 +(3/(b(a−b))) ⇒ b(a−b)=(3/((x−(√2)a^3 ))) if x is minimum, b(a−b) is maximum ⇒ b = (a/2) ⇒ x−(√2)a^3 = ((12)/a^2 ) x = (√2)a^3 +((12)/a^2 ) which has a minimum value when 3(√2)a^2 = ((24)/a^3 ) ⇒ a^5 = ((√2))^5 ⇒ a= (√2) ⇒ x_(min) = 4+((12)/2) = 10 .
$${let}\:\:{x}=\:\sqrt{\mathrm{2}}{a}^{\mathrm{3}} +\frac{\mathrm{3}}{{b}\left({a}−{b}\right)} \\ $$$$\Rightarrow\:\:{b}\left({a}−{b}\right)=\frac{\mathrm{3}}{\left({x}−\sqrt{\mathrm{2}}{a}^{\mathrm{3}} \right)} \\ $$$${if}\:{x}\:{is}\:{minimum},\:{b}\left({a}−{b}\right)\:{is}\:{maximum} \\ $$$$\Rightarrow\:{b}\:=\:\frac{{a}}{\mathrm{2}} \\ $$$$\Rightarrow\:\:{x}−\sqrt{\mathrm{2}}{a}^{\mathrm{3}} \:=\:\frac{\mathrm{12}}{{a}^{\mathrm{2}} } \\ $$$${x}\:=\:\sqrt{\mathrm{2}}{a}^{\mathrm{3}} +\frac{\mathrm{12}}{{a}^{\mathrm{2}} } \\ $$$${which}\:{has}\:{a}\:{minimum}\:{value} \\ $$$${when}\:\:\:\:\mathrm{3}\sqrt{\mathrm{2}}{a}^{\mathrm{2}} \:=\:\frac{\mathrm{24}}{{a}^{\mathrm{3}} } \\ $$$$\Rightarrow\:\:\:\:\:{a}^{\mathrm{5}} \:=\:\left(\sqrt{\mathrm{2}}\right)^{\mathrm{5}} \:\:\:\Rightarrow\:\:{a}=\:\sqrt{\mathrm{2}}\: \\ $$$$\Rightarrow\:\:\:{x}_{{min}} \:=\:\mathrm{4}+\frac{\mathrm{12}}{\mathrm{2}}\:=\:\mathrm{10}\:. \\ $$
Commented by Joel578 last updated on 28/Sep/18
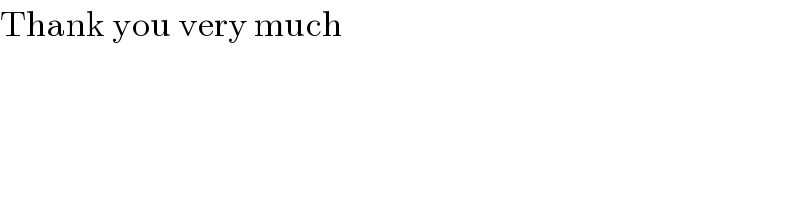
Thank you very much
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 28/Sep/18
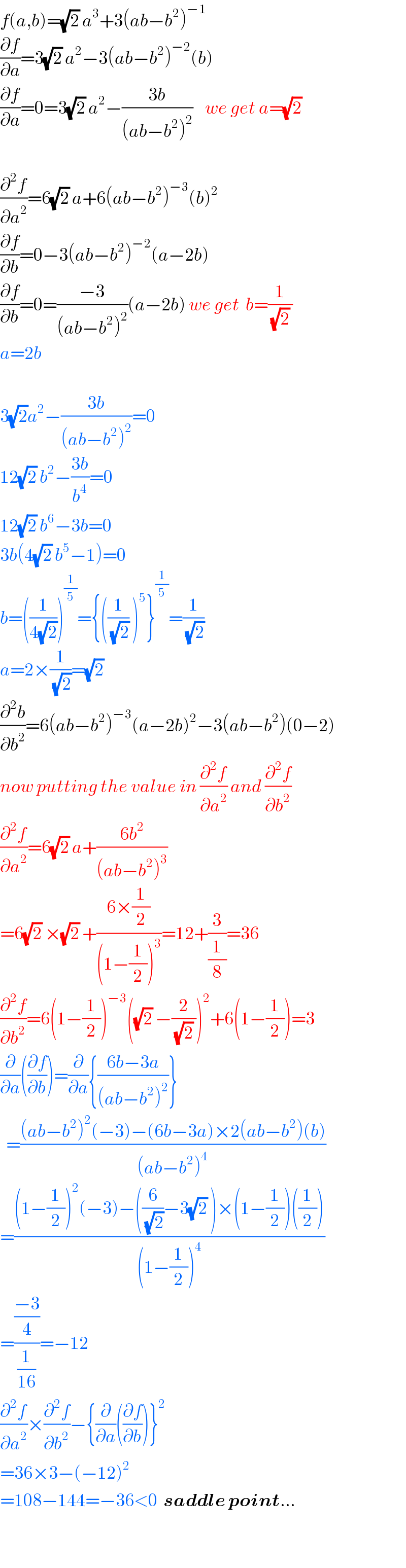
f(a,b)=(√2) a^3 +3(ab−b^2 )^(−1) (∂f/∂a)=3(√2) a^2 −3(ab−b^2 )^(−2) (b) (∂f/∂a)=0=3(√2) a^2 −((3b)/((ab−b^2 )^2 )) we get a=(√2) (∂^2 f/∂a^2 )=6(√2) a+6(ab−b^2 )^(−3) (b)^2 (∂f/∂b)=0−3(ab−b^2 )^(−2) (a−2b) (∂f/∂b)=0=((−3)/((ab−b^2 )^2 ))(a−2b) we get b=(1/( (√2) )) a=2b 3(√2)a^2 −((3b)/((ab−b^2 )^2 ))=0 12(√2) b^2 −((3b)/b^4 )=0 12(√2) b^6 −3b=0 3b(4(√2) b^5 −1)=0 b=((1/(4(√2))))^(1/5) ={((1/( (√2))) )^5 }^(1/5) =(1/( (√2))) a=2×(1/( (√2)))=(√2) (∂^2 b/∂b^2 )=6(ab−b^2 )^(−3) (a−2b)^2 −3(ab−b^2 )(0−2) now putting the value in (∂^2 f/∂a^2 ) and (∂^2 f/∂b^2 ) (∂^2 f/∂a^2 )=6(√2) a+((6b^2 )/((ab−b^2 )^3 )) =6(√2) ×(√2) +((6×(1/2))/((1−(1/2))^3 ))=12+(3/(1/8))=36 (∂^2 f/∂b^2 )=6(1−(1/2))^(−3) ((√2) −(2/( (√2) )))^2 +6(1−(1/2))=3 (∂/∂a)((∂f/∂b))=(∂/∂a){((6b−3a)/((ab−b^2 )^2 ))} =(((ab−b^2 )^2 (−3)−(6b−3a)×2(ab−b^2 )(b))/((ab−b^2 )^4 )) =(((1−(1/2))^2 (−3)−((6/( (√2)))−3(√2) )×(1−(1/2))((1/2)))/((1−(1/2))^4 )) =(((−3)/4)/(1/(16)))=−12 (∂^2 f/∂a^2 )×(∂^2 f/∂b^2 )−{(∂/∂a)((∂f/∂b))}^2 =36×3−(−12)^2 =108−144=−36<0 saddle point...
$${f}\left({a},{b}\right)=\sqrt{\mathrm{2}}\:{a}^{\mathrm{3}} +\mathrm{3}\left({ab}−{b}^{\mathrm{2}} \right)^{−\mathrm{1}} \\ $$$$\frac{\partial{f}}{\partial{a}}=\mathrm{3}\sqrt{\mathrm{2}}\:{a}^{\mathrm{2}} −\mathrm{3}\left({ab}−{b}^{\mathrm{2}} \right)^{−\mathrm{2}} \left({b}\right) \\ $$$$\frac{\partial{f}}{\partial{a}}=\mathrm{0}=\mathrm{3}\sqrt{\mathrm{2}}\:{a}^{\mathrm{2}} −\frac{\mathrm{3}{b}}{\left({ab}−{b}^{\mathrm{2}} \right)^{\mathrm{2}} }\:\:\:\:{we}\:{get}\:{a}=\sqrt{\mathrm{2}}\: \\ $$$$ \\ $$$$\frac{\partial^{\mathrm{2}} {f}}{\partial{a}^{\mathrm{2}} }=\mathrm{6}\sqrt{\mathrm{2}}\:{a}+\mathrm{6}\left({ab}−{b}^{\mathrm{2}} \right)^{−\mathrm{3}} \left({b}\right)^{\mathrm{2}} \\ $$$$\frac{\partial{f}}{\partial{b}}=\mathrm{0}−\mathrm{3}\left({ab}−{b}^{\mathrm{2}} \right)^{−\mathrm{2}} \left({a}−\mathrm{2}{b}\right) \\ $$$$\frac{\partial{f}}{\partial{b}}=\mathrm{0}=\frac{−\mathrm{3}}{\left({ab}−{b}^{\mathrm{2}} \right)^{\mathrm{2}} }\left({a}−\mathrm{2}{b}\right)\:{we}\:{get}\:\:{b}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\:} \\ $$$${a}=\mathrm{2}{b} \\ $$$$ \\ $$$$\mathrm{3}\sqrt{\mathrm{2}}{a}^{\mathrm{2}} −\frac{\mathrm{3}{b}}{\left({ab}−{b}^{\mathrm{2}} \right)^{\mathrm{2}} }=\mathrm{0} \\ $$$$\mathrm{12}\sqrt{\mathrm{2}}\:{b}^{\mathrm{2}} −\frac{\mathrm{3}{b}}{{b}^{\mathrm{4}} }=\mathrm{0} \\ $$$$\mathrm{12}\sqrt{\mathrm{2}}\:{b}^{\mathrm{6}} −\mathrm{3}{b}=\mathrm{0} \\ $$$$\mathrm{3}{b}\left(\mathrm{4}\sqrt{\mathrm{2}}\:{b}^{\mathrm{5}} −\mathrm{1}\right)=\mathrm{0} \\ $$$${b}=\left(\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\right)^{\frac{\mathrm{1}}{\mathrm{5}}} =\left\{\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\right)^{\mathrm{5}} \right\}^{\frac{\mathrm{1}}{\mathrm{5}}} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$${a}=\mathrm{2}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}=\sqrt{\mathrm{2}}\: \\ $$$$\frac{\partial^{\mathrm{2}} {b}}{\partial{b}^{\mathrm{2}} }=\mathrm{6}\left({ab}−{b}^{\mathrm{2}} \right)^{−\mathrm{3}} \left({a}−\mathrm{2}{b}\right)^{\mathrm{2}} −\mathrm{3}\left({ab}−{b}^{\mathrm{2}} \right)\left(\mathrm{0}−\mathrm{2}\right) \\ $$$${now}\:{putting}\:{the}\:{value}\:{in}\:\frac{\partial^{\mathrm{2}} {f}}{\partial{a}^{\mathrm{2}} }\:{and}\:\frac{\partial^{\mathrm{2}} {f}}{\partial{b}^{\mathrm{2}} } \\ $$$$\frac{\partial^{\mathrm{2}} {f}}{\partial{a}^{\mathrm{2}} }=\mathrm{6}\sqrt{\mathrm{2}}\:{a}+\frac{\mathrm{6}{b}^{\mathrm{2}} }{\left({ab}−{b}^{\mathrm{2}} \right)^{\mathrm{3}} } \\ $$$$=\mathrm{6}\sqrt{\mathrm{2}}\:×\sqrt{\mathrm{2}}\:+\frac{\mathrm{6}×\frac{\mathrm{1}}{\mathrm{2}}}{\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{3}} }=\mathrm{12}+\frac{\mathrm{3}}{\frac{\mathrm{1}}{\mathrm{8}}}=\mathrm{36} \\ $$$$\frac{\partial^{\mathrm{2}} {f}}{\partial{b}^{\mathrm{2}} }=\mathrm{6}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{−\mathrm{3}} \left(\sqrt{\mathrm{2}}\:−\frac{\mathrm{2}}{\:\sqrt{\mathrm{2}}\:}\right)^{\mathrm{2}} +\mathrm{6}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{3} \\ $$$$\frac{\partial}{\partial{a}}\left(\frac{\partial{f}}{\partial{b}}\right)=\frac{\partial}{\partial{a}}\left\{\frac{\mathrm{6}{b}−\mathrm{3}{a}}{\left({ab}−{b}^{\mathrm{2}} \right)^{\mathrm{2}} }\right\} \\ $$$$\:\:=\frac{\left({ab}−{b}^{\mathrm{2}} \right)^{\mathrm{2}} \left(−\mathrm{3}\right)−\left(\mathrm{6}{b}−\mathrm{3}{a}\right)×\mathrm{2}\left({ab}−{b}^{\mathrm{2}} \right)\left({b}\right)}{\left({ab}−{b}^{\mathrm{2}} \right)^{\mathrm{4}} } \\ $$$$=\frac{\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \left(−\mathrm{3}\right)−\left(\frac{\mathrm{6}}{\:\sqrt{\mathrm{2}}}−\mathrm{3}\sqrt{\mathrm{2}}\:\right)×\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{4}} } \\ $$$$=\frac{\frac{−\mathrm{3}}{\mathrm{4}}}{\frac{\mathrm{1}}{\mathrm{16}}}=−\mathrm{12} \\ $$$$\frac{\partial^{\mathrm{2}} {f}}{\partial{a}^{\mathrm{2}} }×\frac{\partial^{\mathrm{2}} {f}}{\partial{b}^{\mathrm{2}} }−\left\{\frac{\partial}{\partial{a}}\left(\frac{\partial{f}}{\partial{b}}\right)\right\}^{\mathrm{2}} \\ $$$$=\mathrm{36}×\mathrm{3}−\left(−\mathrm{12}\right)^{\mathrm{2}} \\ $$$$=\mathrm{108}−\mathrm{144}=−\mathrm{36}<\mathrm{0}\:\:\boldsymbol{{saddle}}\:\boldsymbol{{point}}… \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *