Menu Close

Let-a-and-b-be-real-numbers-such-that-sin-a-sin-b-2-2-cos-a-cos-b-6-2-Evaluate-sin-a-b-

Tinku Tara 0 Comments
Pin




Question Number 121689 by bemath last updated on 11/Nov/20
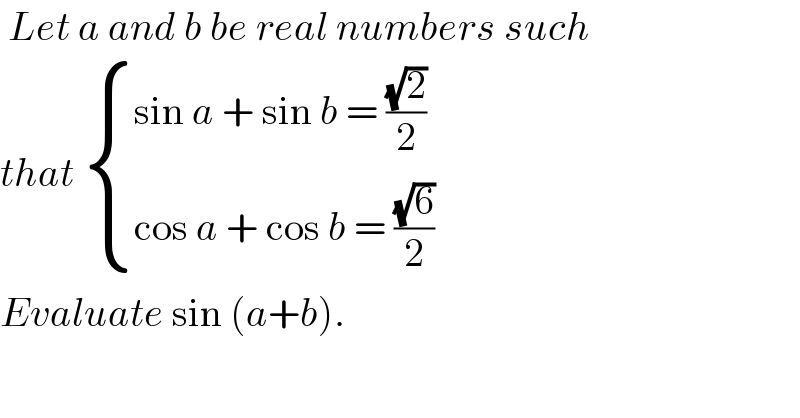
Let a and b be real numbers such that { ((sin a + sin b = ((√2)/2))),((cos a + cos b = ((√6)/2))) :} Evaluate sin (a+b).
$$\:{Let}\:{a}\:{and}\:{b}\:{be}\:{real}\:{numbers}\:{such} \\ $$$${that}\:\begin{cases}{\mathrm{sin}\:{a}\:+\:\mathrm{sin}\:{b}\:=\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}\\{\mathrm{cos}\:{a}\:+\:\mathrm{cos}\:{b}\:=\:\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}}\end{cases} \\ $$$${Evaluate}\:\mathrm{sin}\:\left({a}+{b}\right).\: \\ $$
Answered by liberty last updated on 11/Nov/20
squaring the both equation gives { ((sin^2 a + 2sin a sin b + sin^2 b = (2/4))),((cos^2 a +2 cos a cos b + cos^2 b = (6/4))) :} and add the result to obtain 2 + 2 cos (a−b) = 2 → cos (a−b) = 0 Multiplying the two given relation yields ⇒(sin a + sin b)(cos a+cos b) = ((√3)/2) ⇒sin acos a + sin acos b+sin bcos a+sin bcos b=((√3)/2) ⇒sin 2a + sin 2b+2sin (a+b)= (√3) ⇒2sin (a+b)cos (a−b)+2sin (a+b)=(√3) ⇒2sin (a+b) { cos (a−b)+1 } = (√3) ⇒2sin (a+b) { 0+1 } = (√3) ⇒sin (a+b) = ((√3)/2). ▲
$$\mathrm{squaring}\:\mathrm{the}\:\mathrm{both}\:\mathrm{equation}\:\mathrm{gives} \\ $$$$\begin{cases}{\mathrm{sin}\:^{\mathrm{2}} {a}\:+\:\mathrm{2sin}\:{a}\:\mathrm{sin}\:{b}\:+\:\mathrm{sin}\:^{\mathrm{2}} {b}\:=\:\frac{\mathrm{2}}{\mathrm{4}}}\\{\mathrm{cos}\:^{\mathrm{2}} {a}\:+\mathrm{2}\:\mathrm{cos}\:{a}\:\mathrm{cos}\:{b}\:+\:\mathrm{cos}\:^{\mathrm{2}} {b}\:=\:\frac{\mathrm{6}}{\mathrm{4}}}\end{cases} \\ $$$$\mathrm{and}\:\mathrm{add}\:\mathrm{the}\:\mathrm{result}\:\mathrm{to}\:\mathrm{obtain}\: \\ $$$$\mathrm{2}\:+\:\mathrm{2}\:\mathrm{cos}\:\left({a}−{b}\right)\:=\:\mathrm{2}\:\rightarrow\:\mathrm{cos}\:\left({a}−{b}\right)\:=\:\mathrm{0} \\ $$$$\mathrm{Multiplying}\:\mathrm{the}\:\mathrm{two}\:\mathrm{given}\:\mathrm{relation}\:\mathrm{yields} \\ $$$$\Rightarrow\left(\mathrm{sin}\:{a}\:+\:\mathrm{sin}\:{b}\right)\left(\mathrm{cos}\:{a}+\mathrm{cos}\:{b}\right)\:=\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{sin}\:{a}\mathrm{cos}\:{a}\:+\:\mathrm{sin}\:{a}\mathrm{cos}\:{b}+\mathrm{sin}\:{b}\mathrm{cos}\:{a}+\mathrm{sin}\:{b}\mathrm{cos}\:{b}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{sin}\:\mathrm{2}{a}\:+\:\mathrm{sin}\:\mathrm{2}{b}+\mathrm{2sin}\:\left({a}+{b}\right)=\:\sqrt{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{2sin}\:\left({a}+{b}\right)\mathrm{cos}\:\left({a}−{b}\right)+\mathrm{2sin}\:\left({a}+{b}\right)=\sqrt{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{2sin}\:\left({a}+{b}\right)\:\left\{\:\mathrm{cos}\:\left({a}−{b}\right)+\mathrm{1}\:\right\}\:=\:\sqrt{\mathrm{3}}\: \\ $$$$\Rightarrow\mathrm{2sin}\:\left({a}+{b}\right)\:\left\{\:\mathrm{0}+\mathrm{1}\:\right\}\:=\:\sqrt{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{sin}\:\left({a}+{b}\right)\:=\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}.\:\blacktriangle \\ $$
Answered by TANMAY PANACEA last updated on 11/Nov/20
2sin(((a+b)/2))cos(((a−b)/2))=((√2)/2) 2cos(((a+b)/2))cos(((a−b)/2))=((√6)/2) tan(((a+b)/2))=((√2)/( (√6)))=(1/( (√3)))=tan30^o a+b=60^o sin(a+b)=((√3)/2) Or method or sin(a+b)=((2t)/(1+t^2 )) [t=tan((a+b)/2)] =((2×(1/( (√3))))/(1+((1/( (√3))))^2 ))=((2/( (√3)))/(4/3))=((2×3)/(4×(√3)))=((√3)/2)
$$\mathrm{2}{sin}\left(\frac{{a}+{b}}{\mathrm{2}}\right){cos}\left(\frac{{a}−{b}}{\mathrm{2}}\right)=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$$\mathrm{2}{cos}\left(\frac{{a}+{b}}{\mathrm{2}}\right){cos}\left(\frac{{a}−{b}}{\mathrm{2}}\right)=\frac{\sqrt{\mathrm{6}}}{\mathrm{2}} \\ $$$${tan}\left(\frac{{a}+{b}}{\mathrm{2}}\right)=\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{6}}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}={tan}\mathrm{30}^{{o}} \\ $$$${a}+{b}=\mathrm{60}^{{o}} \\ $$$${sin}\left({a}+{b}\right)=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\boldsymbol{{O}}{r}\:{method} \\ $$$${or}\:{sin}\left({a}+{b}\right)=\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\:\:\left[{t}={tan}\frac{{a}+{b}}{\mathrm{2}}\right] \\ $$$$=\frac{\mathrm{2}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}}{\mathrm{1}+\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} }=\frac{\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}}{\frac{\mathrm{4}}{\mathrm{3}}}=\frac{\mathrm{2}×\mathrm{3}}{\mathrm{4}×\sqrt{\mathrm{3}}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *