Question Number 153988 by mathdanisur last updated on 12/Sep/21
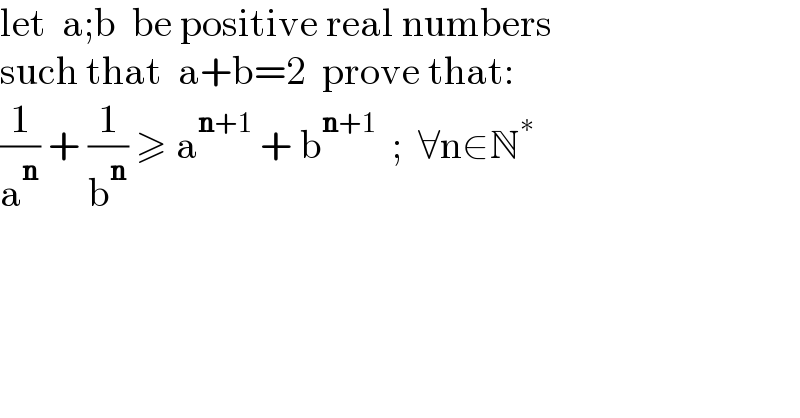
$$\mathrm{let}\:\:\mathrm{a};\mathrm{b}\:\:\mathrm{be}\:\mathrm{positive}\:\mathrm{real}\:\mathrm{numbers} \\ $$$$\mathrm{such}\:\mathrm{that}\:\:\mathrm{a}+\mathrm{b}=\mathrm{2}\:\:\mathrm{prove}\:\mathrm{that}: \\ $$$$\frac{\mathrm{1}}{\mathrm{a}^{\boldsymbol{\mathrm{n}}} }\:+\:\frac{\mathrm{1}}{\mathrm{b}^{\boldsymbol{\mathrm{n}}} }\:\geqslant\:\mathrm{a}^{\boldsymbol{\mathrm{n}}+\mathrm{1}} \:+\:\mathrm{b}^{\boldsymbol{\mathrm{n}}+\mathrm{1}} \:\:;\:\:\forall\mathrm{n}\in\mathbb{N}^{\ast} \\ $$
Answered by metamorfose last updated on 15/Sep/21

$${recurrence} \\ $$
