Question Number 144742 by loveineq last updated on 28/Jun/21
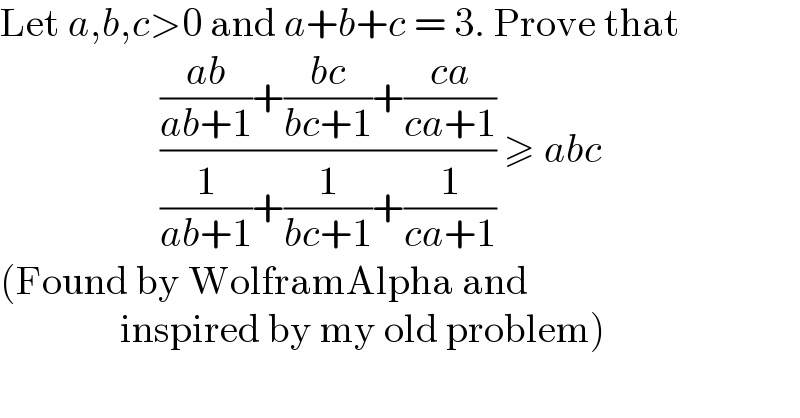
$$\mathrm{Let}\:{a},{b},{c}>\mathrm{0}\:\mathrm{and}\:{a}+{b}+{c}\:=\:\mathrm{3}.\:\mathrm{Prove}\:\mathrm{that}\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\frac{{ab}}{{ab}+\mathrm{1}}+\frac{{bc}}{{bc}+\mathrm{1}}+\frac{{ca}}{{ca}+\mathrm{1}}}{\frac{\mathrm{1}}{{ab}+\mathrm{1}}+\frac{\mathrm{1}}{{bc}+\mathrm{1}}+\frac{\mathrm{1}}{{ca}+\mathrm{1}}}\:\geqslant\:{abc} \\ $$$$\left(\mathrm{Found}\:\mathrm{by}\:\mathrm{WolframAlpha}\:\mathrm{and}\:\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{inspired}\:\mathrm{by}\:\mathrm{my}\:\mathrm{old}\:\mathrm{problem}\right) \\ $$
