Question Number 34713 by abdo mathsup 649 cc last updated on 10/May/18
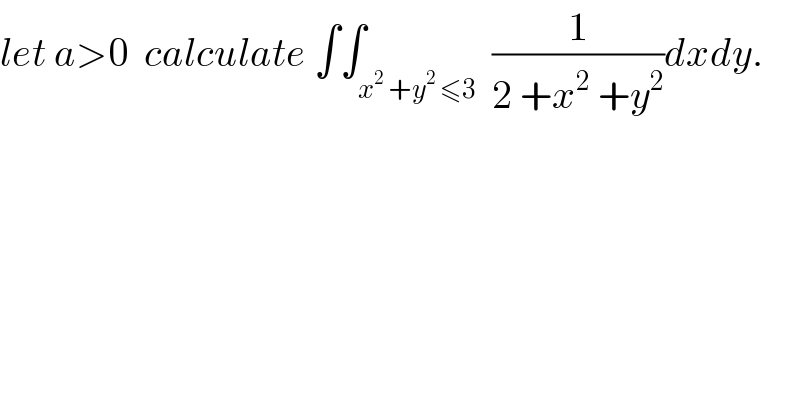
$${let}\:{a}>\mathrm{0}\:\:{calculate}\:\int\int_{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \:\leqslant\mathrm{3}} \:\frac{\mathrm{1}}{\mathrm{2}\:+{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} }{dxdy}. \\ $$
Commented by math khazana by abdo last updated on 11/May/18
![let ude?the diffeomorphisme x=r cosθ , y = r sinθ with 0≤r≤(√3) and −π≤θ≤π I =∫∫_(0≤r≤(√(3 )) and −π≤ θ≤π) (1/(2 +r^2 )) rdr dθ = ∫_0 ^(√3) (r/(2+r^2 )) dr. ∫_(−π) ^π dθ = 2π ∫_0 ^(√3) (r/(2+r^2 ))dr =π[ln(2+r^2 )]_0 ^(√3) = π{ln(5) −ln(2)} .](https://www.tinkutara.com/question/Q34777.png)
$${let}\:{ude}?{the}\:{diffeomorphisme}\:{x}={r}\:{cos}\theta\:, \\ $$$${y}\:=\:{r}\:{sin}\theta\:\:{with}\:\mathrm{0}\leqslant{r}\leqslant\sqrt{\mathrm{3}}\:\:\:{and}\:\:−\pi\leqslant\theta\leqslant\pi \\ $$$${I}\:\:=\int\int_{\mathrm{0}\leqslant{r}\leqslant\sqrt{\mathrm{3}\:}\:{and}\:\:−\pi\leqslant\:\theta\leqslant\pi} \:\:\:\frac{\mathrm{1}}{\mathrm{2}\:+{r}^{\mathrm{2}} }\:{rdr}\:{d}\theta \\ $$$$=\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{3}}} \:\:\frac{{r}}{\mathrm{2}+{r}^{\mathrm{2}} }\:{dr}.\:\int_{−\pi} ^{\pi} \:{d}\theta\:=\:\mathrm{2}\pi\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{3}}} \:\:\:\:\frac{{r}}{\mathrm{2}+{r}^{\mathrm{2}} }{dr} \\ $$$$=\pi\left[{ln}\left(\mathrm{2}+{r}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\sqrt{\mathrm{3}}} \:\:\:=\:\pi\left\{{ln}\left(\mathrm{5}\right)\:−{ln}\left(\mathrm{2}\right)\right\}\:. \\ $$
