Question Number 120528 by snipers237 last updated on 01/Nov/20
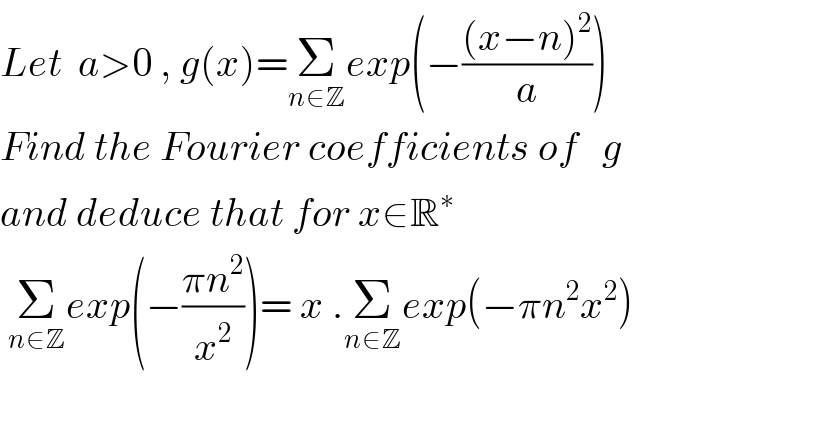
$${Let}\:\:{a}>\mathrm{0}\:,\:{g}\left({x}\right)=\underset{{n}\in\mathbb{Z}} {\sum}{exp}\left(−\frac{\left({x}−{n}\right)^{\mathrm{2}} }{{a}}\right) \\ $$$${Find}\:{the}\:{Fourier}\:{coefficients}\:{of}\:\:\:{g} \\ $$$${and}\:{deduce}\:{that}\:{for}\:{x}\in\mathbb{R}^{\ast} \\ $$$$\:\underset{{n}\in\mathbb{Z}} {\sum}{exp}\left(−\frac{\pi{n}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\right)=\:{x}\:.\underset{{n}\in\mathbb{Z}} {\sum}{exp}\left(−\pi{n}^{\mathrm{2}} {x}^{\mathrm{2}} \right) \\ $$$$ \\ $$
