Question Number 158724 by HongKing last updated on 08/Nov/21
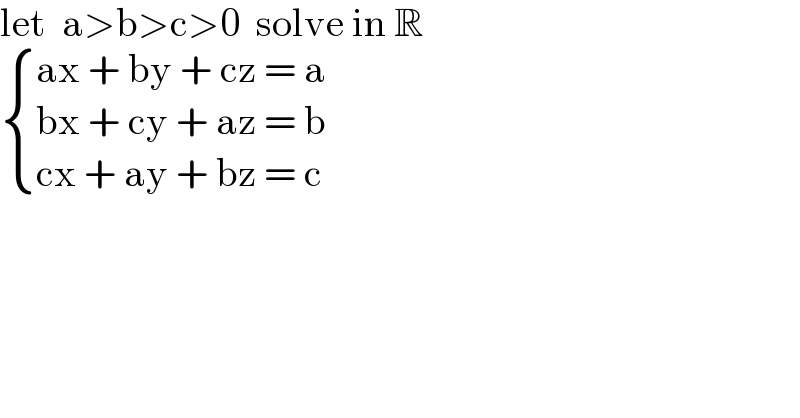
$$\mathrm{let}\:\:\mathrm{a}>\mathrm{b}>\mathrm{c}>\mathrm{0}\:\:\mathrm{solve}\:\mathrm{in}\:\mathbb{R} \\ $$$$\begin{cases}{\mathrm{ax}\:+\:\mathrm{by}\:+\:\mathrm{cz}\:=\:\mathrm{a}}\\{\mathrm{bx}\:+\:\mathrm{cy}\:+\:\mathrm{az}\:=\:\mathrm{b}}\\{\mathrm{cx}\:+\:\mathrm{ay}\:+\:\mathrm{bz}\:=\:\mathrm{c}}\end{cases} \\ $$$$ \\ $$
Answered by ajfour last updated on 08/Nov/21
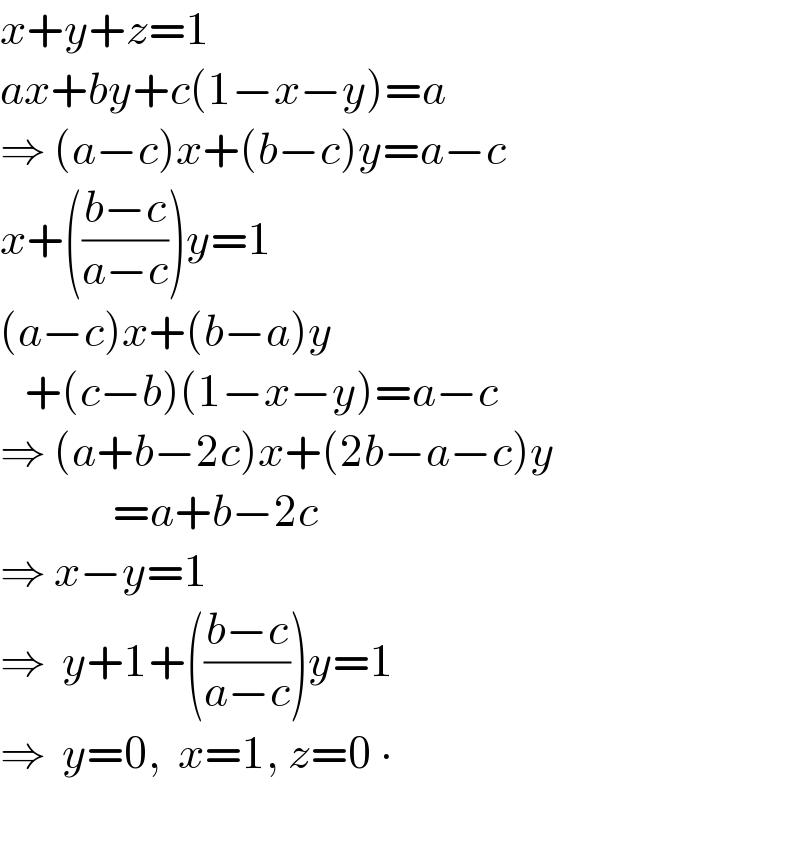
$${x}+{y}+{z}=\mathrm{1} \\ $$$${ax}+{by}+{c}\left(\mathrm{1}−{x}−{y}\right)={a} \\ $$$$\Rightarrow\:\left({a}−{c}\right){x}+\left({b}−{c}\right){y}={a}−{c} \\ $$$${x}+\left(\frac{{b}−{c}}{{a}−{c}}\right){y}=\mathrm{1} \\ $$$$\left({a}−{c}\right){x}+\left({b}−{a}\right){y} \\ $$$$\:\:\:+\left({c}−{b}\right)\left(\mathrm{1}−{x}−{y}\right)={a}−{c} \\ $$$$\Rightarrow\:\left({a}+{b}−\mathrm{2}{c}\right){x}+\left(\mathrm{2}{b}−{a}−{c}\right){y} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:={a}+{b}−\mathrm{2}{c} \\ $$$$\Rightarrow\:{x}−{y}=\mathrm{1} \\ $$$$\Rightarrow\:\:{y}+\mathrm{1}+\left(\frac{{b}−{c}}{{a}−{c}}\right){y}=\mathrm{1} \\ $$$$\Rightarrow\:\:{y}=\mathrm{0},\:\:{x}=\mathrm{1},\:{z}=\mathrm{0}\:\centerdot \\ $$$$ \\ $$
Commented by HongKing last updated on 08/Nov/21
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{dear}\:\mathrm{Ser}\:\mathrm{cool} \\ $$
Answered by som(math1967) last updated on 08/Nov/21
![D= determinant ((a,b,c),(b,c,a),(c,a,b))=a(bc−a^2 )−b(b^2 −ca)+c(ab−c^2 ) =3abc−a^3 −b^3 −c^3 D_1 = determinant ((a,b,c),((b ),c,a),(c,a,b))=abc−a^3 −b^3 +abc+abc−c^3 =3abc−a^3 −b^3 −c^3 D_2 = determinant ((a,a,c),(b,b,a),(c,c,b))=0 [C_(1,) C_2 identical] D_3 = determinant ((a,b,a),(b,c,b),(c,a,c))=0[C_1 ,C_3 identical] x=(D_1 /D)=1,y=(D_2 /D)=0,z=(D_3 /D)=0 a>b>c>0 ∴( 3abc−a^3 −b^3 −c^3 )≠0](https://www.tinkutara.com/question/Q158729.png)
$${D}=\begin{vmatrix}{{a}}&{{b}}&{{c}}\\{{b}}&{{c}}&{{a}}\\{{c}}&{{a}}&{{b}}\end{vmatrix}={a}\left({bc}−{a}^{\mathrm{2}} \right)−{b}\left({b}^{\mathrm{2}} −{ca}\right)+{c}\left({ab}−{c}^{\mathrm{2}} \right) \\ $$$$=\mathrm{3}{abc}−{a}^{\mathrm{3}} −{b}^{\mathrm{3}} −{c}^{\mathrm{3}} \\ $$$${D}_{\mathrm{1}} =\begin{vmatrix}{{a}}&{{b}}&{{c}}\\{{b}\:}&{{c}}&{{a}}\\{{c}}&{{a}}&{{b}}\end{vmatrix}={abc}−{a}^{\mathrm{3}} −{b}^{\mathrm{3}} +{abc}+{abc}−{c}^{\mathrm{3}} \\ $$$$=\mathrm{3}{abc}−{a}^{\mathrm{3}} −{b}^{\mathrm{3}} −{c}^{\mathrm{3}} \\ $$$${D}_{\mathrm{2}} =\begin{vmatrix}{{a}}&{{a}}&{{c}}\\{{b}}&{{b}}&{{a}}\\{{c}}&{{c}}&{{b}}\end{vmatrix}=\mathrm{0}\:\left[{C}_{\mathrm{1},} {C}_{\mathrm{2}} \:{identical}\right] \\ $$$${D}_{\mathrm{3}} =\begin{vmatrix}{{a}}&{{b}}&{{a}}\\{{b}}&{{c}}&{{b}}\\{{c}}&{{a}}&{{c}}\end{vmatrix}=\mathrm{0}\left[{C}_{\mathrm{1}} ,{C}_{\mathrm{3}} \:{identical}\right] \\ $$$${x}=\frac{{D}_{\mathrm{1}} }{{D}}=\mathrm{1},{y}=\frac{{D}_{\mathrm{2}} }{{D}}=\mathrm{0},{z}=\frac{{D}_{\mathrm{3}} }{{D}}=\mathrm{0} \\ $$$${a}>{b}>{c}>\mathrm{0}\:\therefore\left(\:\mathrm{3}{abc}−{a}^{\mathrm{3}} −{b}^{\mathrm{3}} −{c}^{\mathrm{3}} \right)\neq\mathrm{0} \\ $$
Commented by HongKing last updated on 08/Nov/21
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{dear}\:\mathrm{Ser}\:\mathrm{cool} \\ $$
