Question Number 61981 by maxmathsup by imad last updated on 13/Jun/19
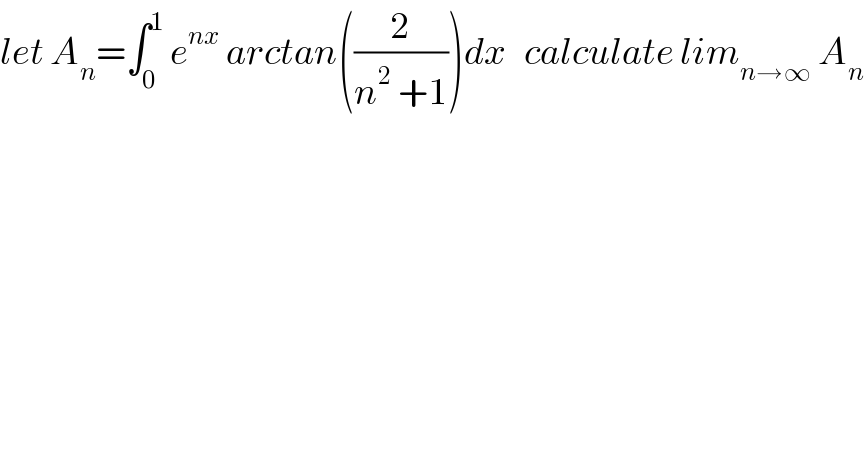
$${let}\:{A}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{{nx}} \:{arctan}\left(\frac{\mathrm{2}}{{n}^{\mathrm{2}} \:+\mathrm{1}}\right){dx}\:\:\:{calculate}\:{lim}_{{n}\rightarrow\infty} \:{A}_{{n}} \\ $$
Commented by maxmathsup by imad last updated on 13/Jun/19
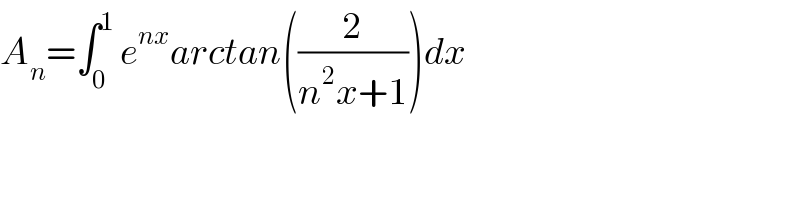
$${A}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{{nx}} {arctan}\left(\frac{\mathrm{2}}{{n}^{\mathrm{2}} {x}+\mathrm{1}}\right){dx}\: \\ $$
