Question Number 104773 by mathmax by abdo last updated on 23/Jul/20
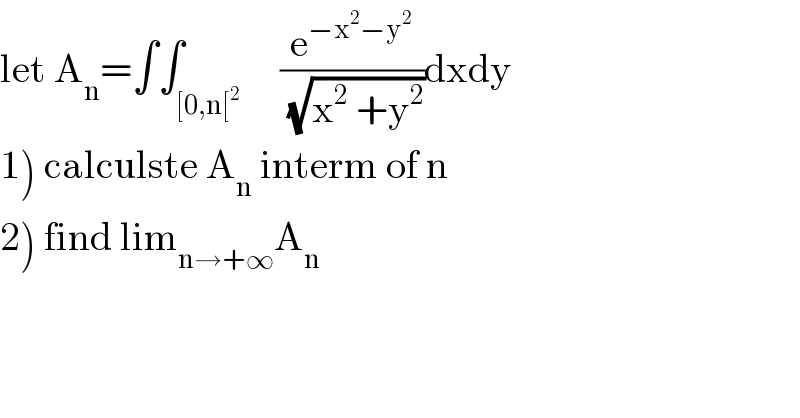
$$\mathrm{let}\:\mathrm{A}_{\mathrm{n}} =\int\int_{\left[\mathrm{0},\mathrm{n}\left[^{\mathrm{2}} \right.\right.} \:\:\:\:\frac{\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} } }{\:\sqrt{\mathrm{x}^{\mathrm{2}} \:+\mathrm{y}^{\mathrm{2}} }}\mathrm{dxdy} \\ $$$$\left.\mathrm{1}\right)\:\mathrm{calculste}\:\mathrm{A}_{\mathrm{n}} \:\mathrm{interm}\:\mathrm{of}\:\mathrm{n} \\ $$$$\left.\mathrm{2}\right)\:\mathrm{find}\:\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{A}_{\mathrm{n}} \\ $$
Answered by mathmax by abdo last updated on 24/Jul/20
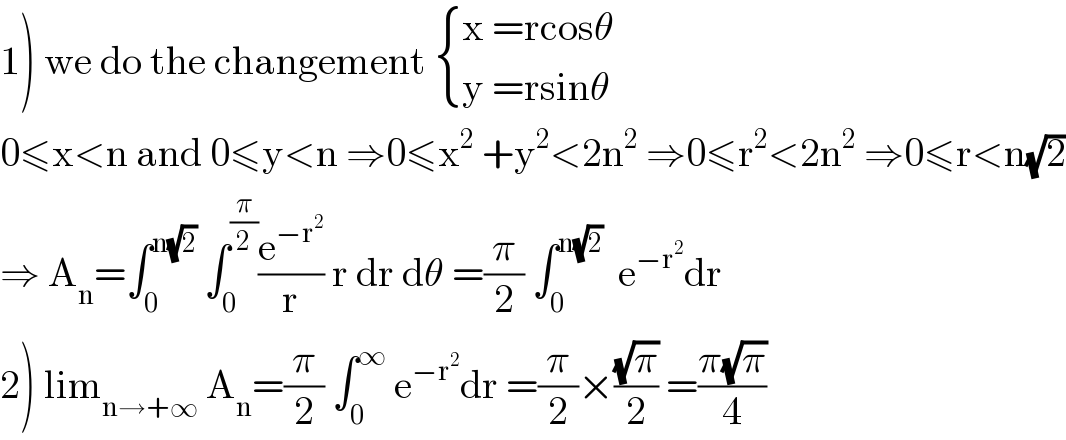
$$\left.\mathrm{1}\right)\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\begin{cases}{\mathrm{x}\:=\mathrm{rcos}\theta}\\{\mathrm{y}\:=\mathrm{rsin}\theta}\end{cases} \\ $$$$\mathrm{0}\leqslant\mathrm{x}<\mathrm{n}\:\mathrm{and}\:\mathrm{0}\leqslant\mathrm{y}<\mathrm{n}\:\Rightarrow\mathrm{0}\leqslant\mathrm{x}^{\mathrm{2}} \:+\mathrm{y}^{\mathrm{2}} <\mathrm{2n}^{\mathrm{2}} \:\Rightarrow\mathrm{0}\leqslant\mathrm{r}^{\mathrm{2}} <\mathrm{2n}^{\mathrm{2}} \:\Rightarrow\mathrm{0}\leqslant\mathrm{r}<\mathrm{n}\sqrt{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{A}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{n}\sqrt{\mathrm{2}}} \:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{e}^{−\mathrm{r}^{\mathrm{2}} } }{\mathrm{r}}\:\mathrm{r}\:\mathrm{dr}\:\mathrm{d}\theta\:=\frac{\pi}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\mathrm{n}\sqrt{\mathrm{2}}} \:\:\mathrm{e}^{−\mathrm{r}^{\mathrm{2}} } \mathrm{dr} \\ $$$$\left.\mathrm{2}\right)\:\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\mathrm{A}_{\mathrm{n}} =\frac{\pi}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{r}^{\mathrm{2}} } \mathrm{dr}\:=\frac{\pi}{\mathrm{2}}×\frac{\sqrt{\pi}}{\mathrm{2}}\:=\frac{\pi\sqrt{\pi}}{\mathrm{4}} \\ $$
