Menu Close

let-a-n-1-2-a-n-a-0-2-find-lim-n-a-n-1-

Tinku Tara 0 Comments
Pin




Question Number 93892 by frc2crc last updated on 15/May/20
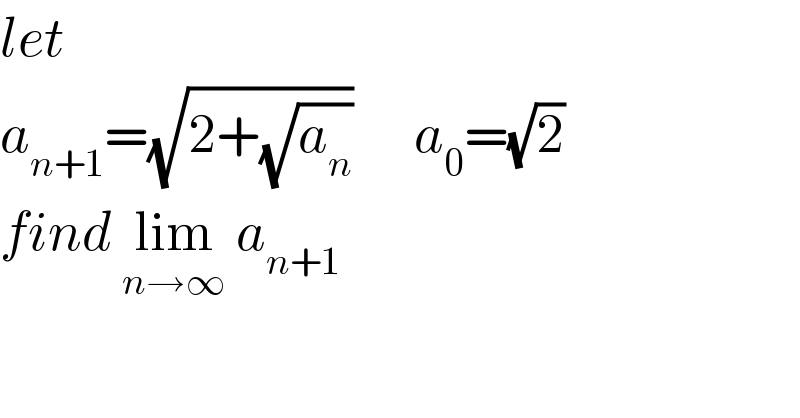
let a_(n+1) =(√(2+(√a_n ))) a_0 =(√2) find lim_(n→∞) a_(n+1)
$${let} \\ $$$${a}_{{n}+\mathrm{1}} =\sqrt{\mathrm{2}+\sqrt{{a}_{{n}} }}\:\:\:\:\:\:{a}_{\mathrm{0}} =\sqrt{\mathrm{2}} \\ $$$${find}\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{a}_{{n}+\mathrm{1}} \\ $$
Commented by Tony Lin last updated on 16/May/20
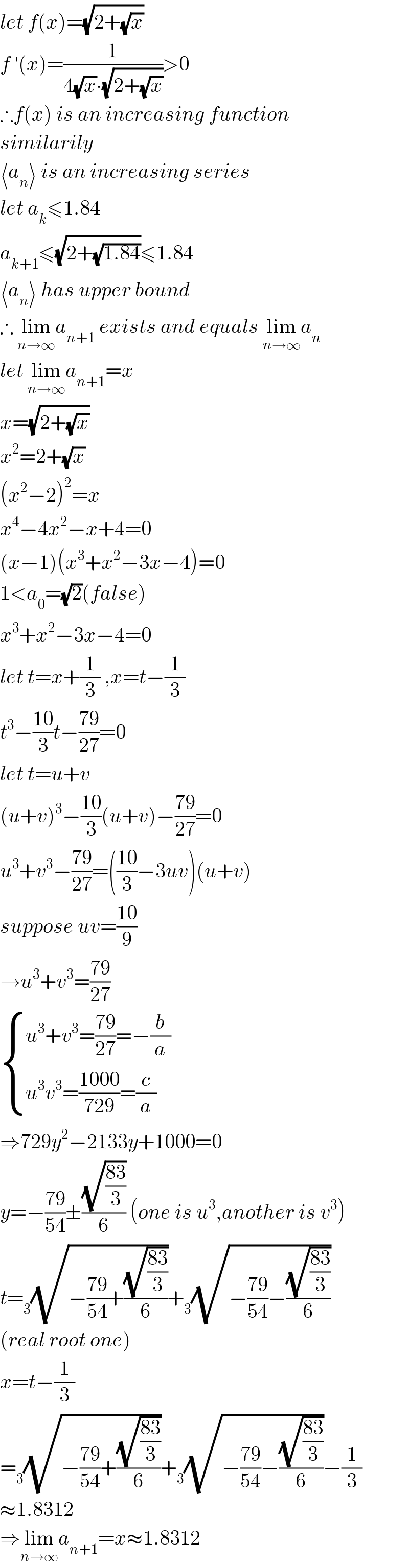
let f(x)=(√(2+(√x))) f ′(x)=(1/(4(√x)∙(√(2+(√x)))))>0 ∴f(x) is an increasing function similarily ⟨a_n ⟩ is an increasing series let a_k ≤1.84 a_(k+1) ≤(√(2+(√(1.84))))≤1.84 ⟨a_n ⟩ has upper bound ∴ lim_(n→∞) a_(n+1) exists and equals lim_(n→∞) a_n let lim_(n→∞) a_(n+1) =x x=(√(2+(√x))) x^2 =2+(√x) (x^2 −2)^2 =x x^4 −4x^2 −x+4=0 (x−1)(x^3 +x^2 −3x−4)=0 1<a_0 =(√2)(false) x^3 +x^2 −3x−4=0 let t=x+(1/3) ,x=t−(1/3) t^3 −((10)/3)t−((79)/(27))=0 let t=u+v (u+v)^3 −((10)/3)(u+v)−((79)/(27))=0 u^3 +v^3 −((79)/(27))=(((10)/3)−3uv)(u+v) suppose uv=((10)/9) →u^3 +v^3 =((79)/(27)) { ((u^3 +v^3 =((79)/(27))=−(b/a))),((u^3 v^3 =((1000)/(729))=(c/a))) :} ⇒729y^2 −2133y+1000=0 y=−((79)/(54))±((√((83)/3))/6) (one is u^3 ,another is v^3 ) t=_3 (√(−((79)/(54))+((√((83)/3))/6)))+_3 (√(−((79)/(54))−((√((83)/3))/6))) (real root one) x=t−(1/3) =_3 (√(−((79)/(54))+((√((83)/3))/6)))+_3 (√(−((79)/(54))−((√((83)/3))/6)))−(1/3) ≈1.8312 ⇒lim_(n→∞) a_(n+1) =x≈1.8312
$${let}\:{f}\left({x}\right)=\sqrt{\mathrm{2}+\sqrt{{x}}} \\ $$$${f}\:'\left({x}\right)=\frac{\mathrm{1}}{\mathrm{4}\sqrt{{x}}\centerdot\sqrt{\mathrm{2}+\sqrt{{x}}}}>\mathrm{0} \\ $$$$\therefore{f}\left({x}\right)\:{is}\:{an}\:{increasing}\:{function} \\ $$$${similarily} \\ $$$$\langle{a}_{{n}} \rangle\:{is}\:{an}\:{increasing}\:{series} \\ $$$${let}\:{a}_{{k}} \leqslant\mathrm{1}.\mathrm{84} \\ $$$${a}_{{k}+\mathrm{1}} \leqslant\sqrt{\mathrm{2}+\sqrt{\mathrm{1}.\mathrm{84}}}\leqslant\mathrm{1}.\mathrm{84} \\ $$$$\langle{a}_{{n}} \rangle\:{has}\:{upper}\:{bound} \\ $$$$\therefore\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}{a}_{{n}+\mathrm{1}} \:{exists}\:{and}\:{equals}\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}{a}_{{n}} \\ $$$${let}\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}{a}_{{n}+\mathrm{1}} ={x} \\ $$$${x}=\sqrt{\mathrm{2}+\sqrt{{x}}} \\ $$$${x}^{\mathrm{2}} =\mathrm{2}+\sqrt{{x}} \\ $$$$\left({x}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} ={x} \\ $$$${x}^{\mathrm{4}} −\mathrm{4}{x}^{\mathrm{2}} −{x}+\mathrm{4}=\mathrm{0} \\ $$$$\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{3}} +{x}^{\mathrm{2}} −\mathrm{3}{x}−\mathrm{4}\right)=\mathrm{0} \\ $$$$\mathrm{1}<{a}_{\mathrm{0}} =\sqrt{\mathrm{2}}\left({false}\right) \\ $$$${x}^{\mathrm{3}} +{x}^{\mathrm{2}} −\mathrm{3}{x}−\mathrm{4}=\mathrm{0} \\ $$$${let}\:{t}={x}+\frac{\mathrm{1}}{\mathrm{3}}\:,{x}={t}−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${t}^{\mathrm{3}} −\frac{\mathrm{10}}{\mathrm{3}}{t}−\frac{\mathrm{79}}{\mathrm{27}}=\mathrm{0} \\ $$$${let}\:{t}={u}+{v} \\ $$$$\left({u}+{v}\right)^{\mathrm{3}} −\frac{\mathrm{10}}{\mathrm{3}}\left({u}+{v}\right)−\frac{\mathrm{79}}{\mathrm{27}}=\mathrm{0} \\ $$$${u}^{\mathrm{3}} +{v}^{\mathrm{3}} −\frac{\mathrm{79}}{\mathrm{27}}=\left(\frac{\mathrm{10}}{\mathrm{3}}−\mathrm{3}{uv}\right)\left({u}+{v}\right) \\ $$$${suppose}\:{uv}=\frac{\mathrm{10}}{\mathrm{9}} \\ $$$$\rightarrow{u}^{\mathrm{3}} +{v}^{\mathrm{3}} =\frac{\mathrm{79}}{\mathrm{27}} \\ $$$$\begin{cases}{{u}^{\mathrm{3}} +{v}^{\mathrm{3}} =\frac{\mathrm{79}}{\mathrm{27}}=−\frac{{b}}{{a}}}\\{{u}^{\mathrm{3}} {v}^{\mathrm{3}} =\frac{\mathrm{1000}}{\mathrm{729}}=\frac{{c}}{{a}}}\end{cases} \\ $$$$\Rightarrow\mathrm{729}{y}^{\mathrm{2}} −\mathrm{2133}{y}+\mathrm{1000}=\mathrm{0} \\ $$$${y}=−\frac{\mathrm{79}}{\mathrm{54}}\pm\frac{\sqrt{\frac{\mathrm{83}}{\mathrm{3}}}}{\mathrm{6}}\:\left({one}\:{is}\:{u}^{\mathrm{3}} ,{another}\:{is}\:{v}^{\mathrm{3}} \right) \\ $$$${t}=_{\mathrm{3}} \sqrt{−\frac{\mathrm{79}}{\mathrm{54}}+\frac{\sqrt{\frac{\mathrm{83}}{\mathrm{3}}}}{\mathrm{6}}}+_{\mathrm{3}} \sqrt{−\frac{\mathrm{79}}{\mathrm{54}}−\frac{\sqrt{\frac{\mathrm{83}}{\mathrm{3}}}}{\mathrm{6}}} \\ $$$$\left({real}\:{root}\:{one}\right) \\ $$$${x}={t}−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$=_{\mathrm{3}} \sqrt{−\frac{\mathrm{79}}{\mathrm{54}}+\frac{\sqrt{\frac{\mathrm{83}}{\mathrm{3}}}}{\mathrm{6}}}+_{\mathrm{3}} \sqrt{−\frac{\mathrm{79}}{\mathrm{54}}−\frac{\sqrt{\frac{\mathrm{83}}{\mathrm{3}}}}{\mathrm{6}}}−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\approx\mathrm{1}.\mathrm{8312} \\ $$$$\Rightarrow\underset{{n}\rightarrow\infty} {\mathrm{lim}}{a}_{{n}+\mathrm{1}} ={x}\approx\mathrm{1}.\mathrm{8312} \\ $$
Commented by Tony Lin last updated on 16/May/20
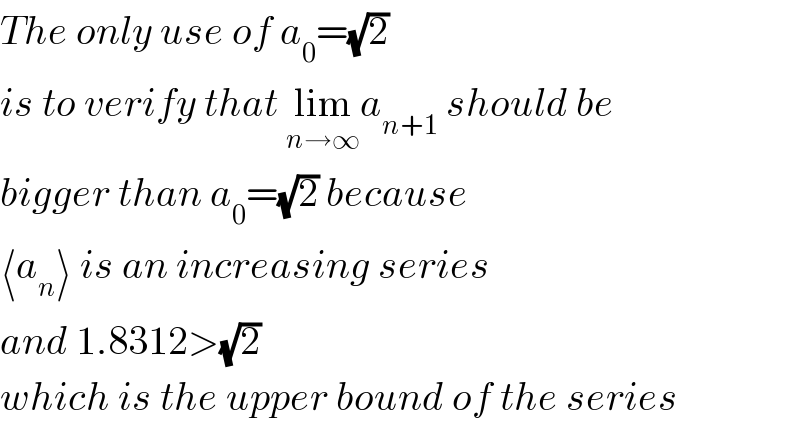
The only use of a_0 =(√2) is to verify that lim_(n→∞) a_(n+1) should be bigger than a_0 =(√2) because ⟨a_n ⟩ is an increasing series and 1.8312>(√2) which is the upper bound of the series
$${The}\:{only}\:{use}\:{of}\:{a}_{\mathrm{0}} =\sqrt{\mathrm{2}}\:\: \\ $$$${is}\:{to}\:{verify}\:{that}\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}{a}_{{n}+\mathrm{1}} \:{should}\:{be} \\ $$$${bigger}\:{than}\:{a}_{\mathrm{0}} =\sqrt{\mathrm{2}}\:{because} \\ $$$$\langle{a}_{{n}} \rangle\:{is}\:{an}\:{increasing}\:{series} \\ $$$${and}\:\mathrm{1}.\mathrm{8312}>\sqrt{\mathrm{2}} \\ $$$${which}\:{is}\:{the}\:{upper}\:{bound}\:{of}\:{the}\:{series} \\ $$
Commented by frc2crc last updated on 16/May/20
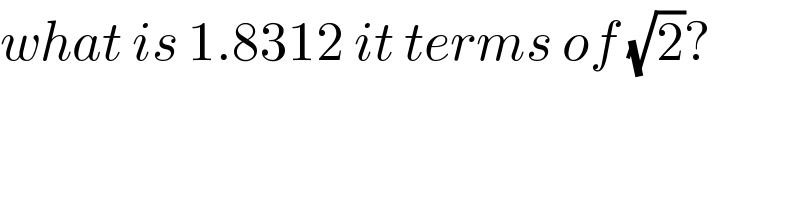
what is 1.8312 it terms of (√2)?
$${what}\:{is}\:\mathrm{1}.\mathrm{8312}\:{it}\:{terms}\:{of}\:\sqrt{\mathrm{2}}? \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *