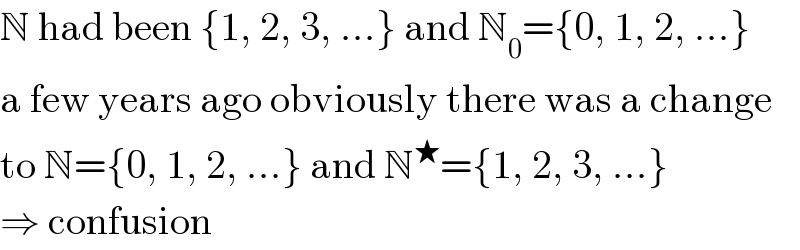Let-A-n-2n-n-N-and-B-2n-3n-n-N-Then-A-B-is-equal-to-

Question Number 114235 by Aina Samuel Temidayo last updated on 18/Sep/20

Let A = {(n, 2 n) : n \in N} and

B = {(2 n, 3 n) : n \in N} . Then A \cap B is

equal to

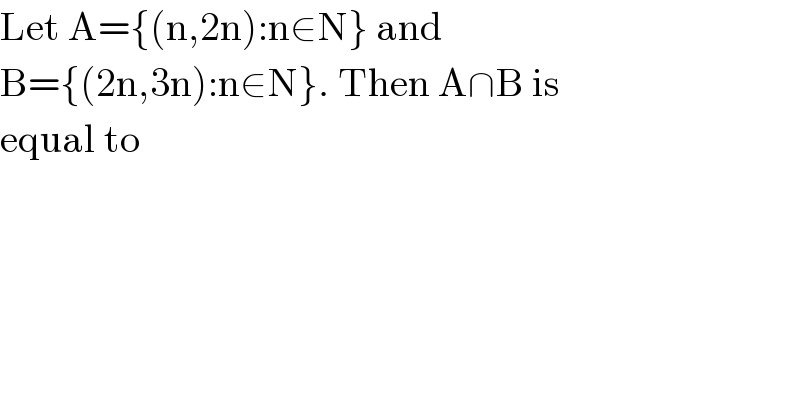
Answered by 1549442205PVT last updated on 18/Sep/20

A \cap B = (0, 0) since

(0, 0) = (0; 2.0) = (2.0; 3.0)

Commented by Aina Samuel Temidayo last updated on 18/Sep/20

Not correct .

Commented by MJS_new last updated on 18/Sep/20

then {what}^{'} s correct ?

Commented by 1549442205PVT last updated on 18/Sep/20

Since N = {0, 1, 2, \dots}, (0, 0) can be

represented under two forms : (n, 2 n)

and (2 n, 3 n)

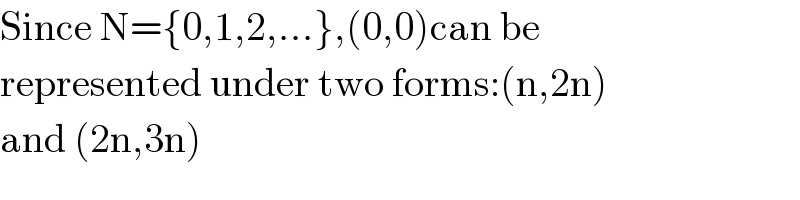
Answered by malwaan last updated on 18/Sep/20

(n_{1}, 2 n_{1}) = (2 n_{2}, 3 n_{2})

n_{1} = 2 n_{2}

2 n_{1} = 3 n_{2} \Rightarrow n_{2} = \frac{2 n_{1}}{3}

∴ n_{1} = 2 (\frac{2 n_{1}}{3}) = \frac{4 n_{1}}{3}

n_{1} (1 - \frac{4}{3}) = 0

(- \frac{1}{3}) n_{1} = 0 \Rightarrow n_{1} = 0 \Rightarrow n_{2} = 0

∴ A \cap B = (0, 0)

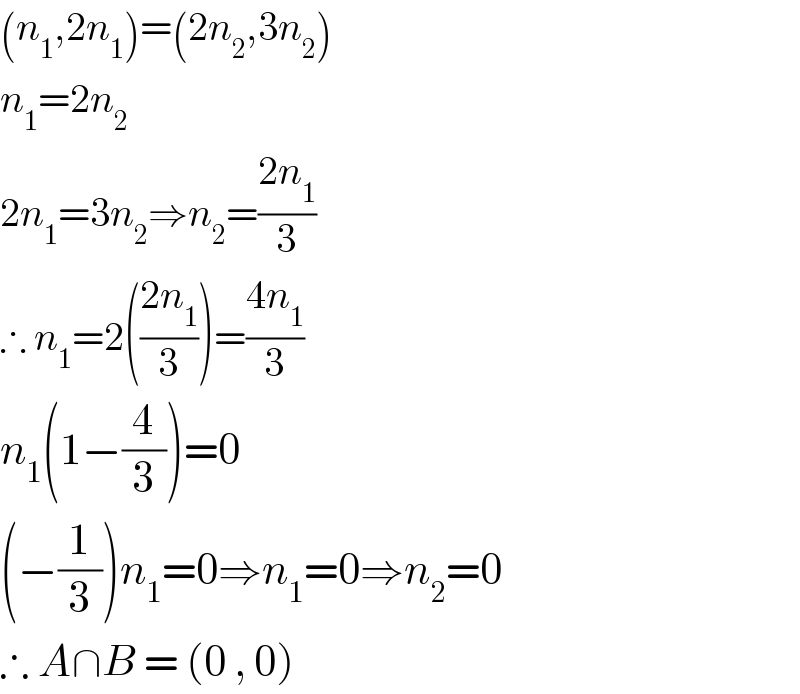
Commented by Aina Samuel Temidayo last updated on 19/Sep/20

Exactly, it was stated in the question .

Commented by 1549442205PVT last updated on 18/Sep/20

Thank for your detail solution . We

can also argue in following way :

For n \neq 0 then (n, 2 n) \neq (2 n, 3 n)

For n = 0 then (n, 2 n) = (2 n, 3 n)

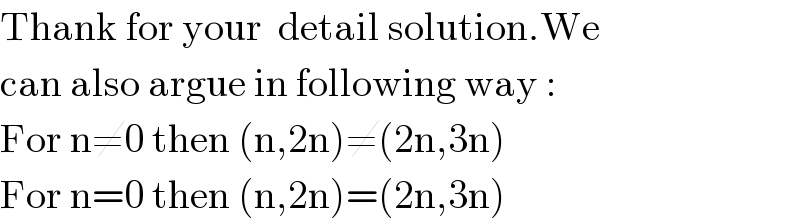
Commented by Rasheed.Sindhi last updated on 18/Sep/20

P e r h a p s t h e s o u r c e o f t h e

q u e s t i o n c o n s i d e r s :

N = {1, 2, 3, \dots}

I n t h a t c a s e A \cap B = \emptyset

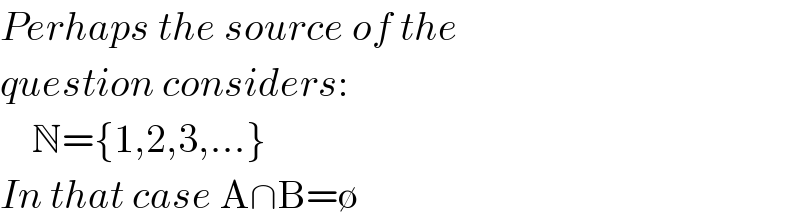
Commented by MJS_new last updated on 19/Sep/20

N had been {1, 2, 3, \dots} and N_{0} = {0, 1, 2, \dots}

a few years ago obviously there was a change

to N = {0, 1, 2, \dots} and N^{★} = {1, 2, 3, \dots}

\Rightarrow confusion

Facebook Tweet Pin