Question Number 130064 by mathmax by abdo last updated on 22/Jan/21
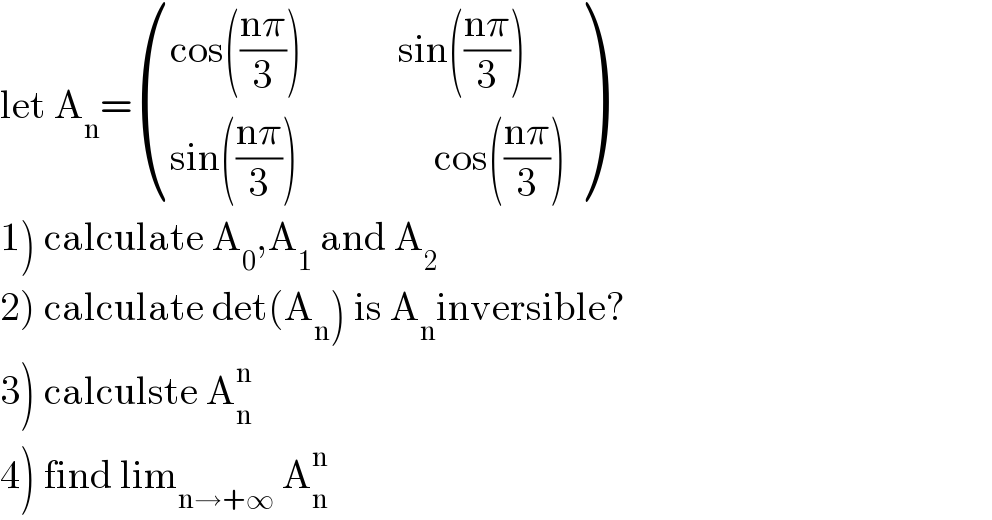
$$\mathrm{let}\:\mathrm{A}_{\mathrm{n}} =\begin{pmatrix}{\mathrm{cos}\left(\frac{\mathrm{n}\pi}{\mathrm{3}}\right)\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{sin}\left(\frac{\mathrm{n}\pi}{\mathrm{3}}\right)}\\{\mathrm{sin}\left(\frac{\mathrm{n}\pi}{\mathrm{3}}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{cos}\left(\frac{\mathrm{n}\pi}{\mathrm{3}}\right)}\end{pmatrix} \\ $$$$\left.\mathrm{1}\right)\:\mathrm{calculate}\:\mathrm{A}_{\mathrm{0}} ,\mathrm{A}_{\mathrm{1}} \:\mathrm{and}\:\mathrm{A}_{\mathrm{2}} \\ $$$$\left.\mathrm{2}\right)\:\mathrm{calculate}\:\mathrm{det}\left(\mathrm{A}_{\mathrm{n}} \right)\:\mathrm{is}\:\mathrm{A}_{\mathrm{n}} \mathrm{inversible}? \\ $$$$\left.\mathrm{3}\right)\:\mathrm{calculste}\:\mathrm{A}_{\mathrm{n}} ^{\mathrm{n}} \\ $$$$\left.\mathrm{4}\right)\:\mathrm{find}\:\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\mathrm{A}_{\mathrm{n}} ^{\mathrm{n}} \\ $$
