Question Number 47857 by maxmathsup by imad last updated on 15/Nov/18
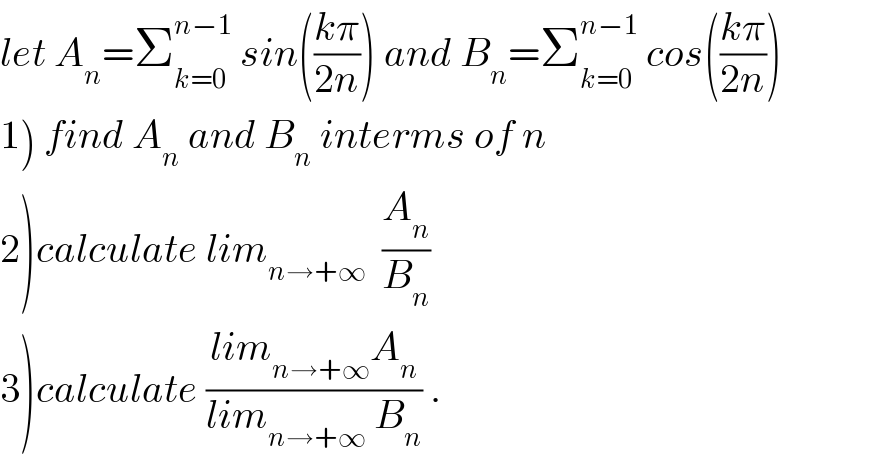
$${let}\:{A}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:{sin}\left(\frac{{k}\pi}{\mathrm{2}{n}}\right)\:{and}\:{B}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:{cos}\left(\frac{{k}\pi}{\mathrm{2}{n}}\right) \\ $$$$\left.\mathrm{1}\right)\:{find}\:{A}_{{n}} \:{and}\:{B}_{{n}} \:{interms}\:{of}\:{n} \\ $$$$\left.\mathrm{2}\right){calculate}\:{lim}_{{n}\rightarrow+\infty} \:\:\frac{{A}_{{n}} }{{B}_{{n}} } \\ $$$$\left.\mathrm{3}\right){calculate}\:\frac{{lim}_{{n}\rightarrow+\infty} {A}_{{n}} }{{lim}_{{n}\rightarrow+\infty\:\:} {B}_{{n}} }\:. \\ $$
Commented by maxmathsup by imad last updated on 17/Nov/18

$${we}\:{have}\:{B}_{{n}} +{iA}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:{e}^{{i}\frac{{k}\pi}{\mathrm{2}{n}}} \:=\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\left({e}^{{i}\frac{\pi}{\mathrm{2}{n}}} \right)^{{k}} \:=\:\frac{\mathrm{1}−{e}^{\frac{{i}\pi}{\mathrm{2}}} }{\mathrm{1}−{e}^{\frac{{i}\pi}{\mathrm{2}{n}}} } \\ $$$$=\frac{\mathrm{1}−{i}}{\mathrm{1}−{cos}\left(\frac{\pi}{\mathrm{2}{n}}\right)−{isin}\left(\frac{\pi}{\mathrm{2}{n}}\right)}\:=\frac{\mathrm{1}−{i}}{\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{4}{n}}\right)−\mathrm{2}{isin}\left(\frac{\pi}{\mathrm{4}{n}}\right){cos}\left(\frac{\pi}{\mathrm{4}{n}}\right)} \\ $$$$=\frac{\mathrm{1}−{i}}{−\mathrm{2}{i}\:{sin}\left(\frac{\pi}{\mathrm{4}{n}}\right)\left({cos}\left(\frac{\pi}{\mathrm{4}{n}}\right)+{i}\:{sin}\left(\frac{\pi}{\mathrm{4}{n}}\right)\right)} \\ $$$$=\frac{{i}+\mathrm{1}}{\mathrm{2}{sin}\left(\frac{\pi}{\mathrm{4}{n}}\right)}\:{e}^{−\frac{{i}\pi}{\mathrm{4}{n}}} \:=\frac{\mathrm{1}+{i}}{\mathrm{2}{sin}\left(\frac{\pi}{\mathrm{4}{n}}\right)}\left\{{cos}\left(\frac{\pi}{\mathrm{4}{n}}\right)−{i}\:{sin}\left(\frac{\pi}{\mathrm{4}{n}}\right)\right\} \\ $$$$=\frac{{cos}\left(\frac{\pi}{\mathrm{4}{n}}\right)−{i}\:{sin}\left(\frac{\pi}{\mathrm{4}{n}}\right)\:+{i}\:{cos}\left(\frac{\pi}{\mathrm{4}{n}}\right)\:+{sin}\left(\frac{\pi}{\mathrm{4}{n}}\right)}{\mathrm{2}{sin}\left(\frac{\pi}{\mathrm{4}{n}}\right)}\:\Rightarrow \\ $$$${B}_{{n}} =\frac{{cos}\left(\frac{\pi}{\mathrm{4}{n}}\right)+{sin}\left(\frac{\pi}{\mathrm{4}{n}}\right)}{\mathrm{2}{sin}\left(\frac{\pi}{\mathrm{4}{n}}\right)}\:=\frac{\mathrm{1}}{\mathrm{2}{tan}\left(\frac{\pi}{\mathrm{4}{n}}\right)}\:+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${A}_{{n}} =\frac{{cos}\left(\frac{\pi}{\mathrm{4}{n}}\right)−{sin}\left(\frac{\pi}{\mathrm{4}{n}}\right)}{\mathrm{2}{sin}\left(\frac{\pi}{\mathrm{4}{n}}\right)}\:=\:\frac{\mathrm{1}}{\mathrm{2}\:{tan}\left(\frac{\pi}{\mathrm{4}{n}}\right)}\:−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\left.\mathrm{2}\right)\:{we}\:{have}\:\frac{{A}_{{n}} }{{B}_{{n}} }\:=\frac{{cos}\left(\frac{\pi}{\mathrm{4}{n}}\right)−{sin}\left(\frac{\pi}{\mathrm{4}{n}}\right)}{{cos}\left(\frac{\pi}{\mathrm{4}{n}}\right)+{sin}\left(\frac{\pi}{\mathrm{4}{n}}\right)}\:\sim\frac{\mathrm{1}−\frac{\pi^{\mathrm{2}} }{\mathrm{32}{n}^{\mathrm{2}} }−\frac{\pi}{\mathrm{4}{n}}}{\mathrm{1}−\frac{\pi^{\mathrm{2}} }{\mathrm{32}{n}^{\mathrm{2}} }+\frac{\pi}{\mathrm{4}{n}}}\:\rightarrow\mathrm{1}\:\left({n}\rightarrow+\infty\right)\:\Rightarrow \\ $$$${lim}_{{n}\rightarrow+\infty} \:\:\:\frac{{A}_{{n}} }{{B}_{{n}} }\:=\mathrm{1}\:. \\ $$
