Question Number 35688 by prof Abdo imad last updated on 22/May/18
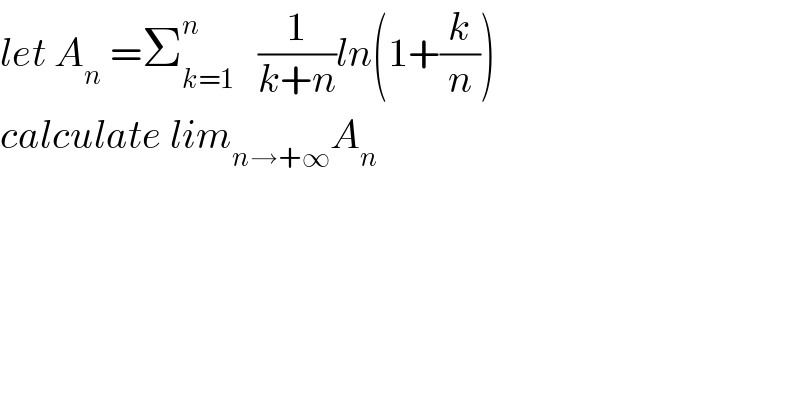
$${let}\:{A}_{{n}} \:=\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\:\frac{\mathrm{1}}{{k}+{n}}{ln}\left(\mathrm{1}+\frac{{k}}{{n}}\right) \\ $$$${calculate}\:{lim}_{{n}\rightarrow+\infty} {A}_{{n}} \\ $$
Commented by prof Abdo imad last updated on 22/May/18
![we have A_n = Σ_(k=1) ^n (1/(n( (k/n) +1)))ln(1+(k/n)) = (1/n) Σ_(k=1) ^n ((ln(1+(k/n)))/(1+(k/n))) so A_n is a Rieman sum lim_(n→+∞) A_n = ∫_0 ^1 ((ln(1+x))/(1+x))dx =I by parts I =[ ln^2 (1+x)]_0 ^1 −∫_0 ^1 ((ln(1+x))/(1+x))dx = {ln(2)}^2 −I ⇒ 2I = {ln(2)}^2 ⇒ I =(({ln(2)}^2 )/2) =lim_(n→+∞) A_n ⇒](https://www.tinkutara.com/question/Q35719.png)
$${we}\:{have}\:{A}_{{n}} \:\:=\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\frac{\mathrm{1}}{{n}\left(\:\frac{{k}}{{n}}\:+\mathrm{1}\right)}{ln}\left(\mathrm{1}+\frac{{k}}{{n}}\right) \\ $$$$=\:\frac{\mathrm{1}}{{n}}\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\:\:\frac{{ln}\left(\mathrm{1}+\frac{{k}}{{n}}\right)}{\mathrm{1}+\frac{{k}}{{n}}}\:{so}\:{A}_{{n}} \:\:{is}\:{a}\:{Rieman}\:{sum} \\ $$$${lim}_{{n}\rightarrow+\infty} \:{A}_{{n}} \:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{ln}\left(\mathrm{1}+{x}\right)}{\mathrm{1}+{x}}{dx}\:={I} \\ $$$$\:{by}\:{parts}\:\:{I}\:\:=\left[\:{ln}^{\mathrm{2}} \left(\mathrm{1}+{x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{ln}\left(\mathrm{1}+{x}\right)}{\mathrm{1}+{x}}{dx} \\ $$$$=\:\left\{{ln}\left(\mathrm{2}\right)\right\}^{\mathrm{2}} \:−{I}\:\Rightarrow\:\mathrm{2}{I}\:=\:\left\{{ln}\left(\mathrm{2}\right)\right\}^{\mathrm{2}} \:\Rightarrow \\ $$$${I}\:=\frac{\left\{{ln}\left(\mathrm{2}\right)\right\}^{\mathrm{2}} }{\mathrm{2}}\:={lim}_{{n}\rightarrow+\infty} \:{A}_{{n}} \\ $$$$\Rightarrow\: \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 22/May/18
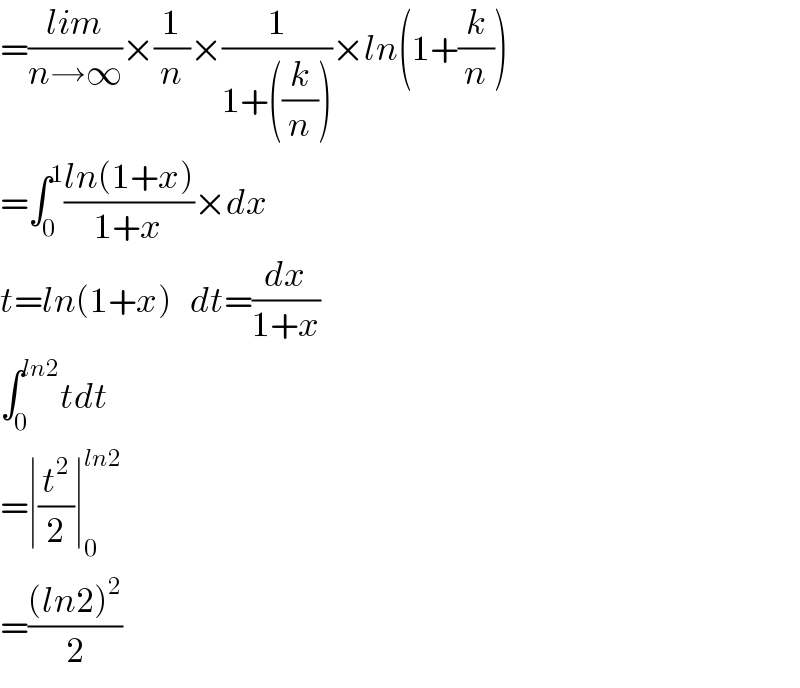
$$=\frac{{lim}}{{n}\rightarrow\infty}×\frac{\mathrm{1}}{{n}}×\frac{\mathrm{1}}{\mathrm{1}+\left(\frac{{k}}{{n}}\right)}×{ln}\left(\mathrm{1}+\frac{{k}}{{n}}\right) \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{x}\right)}{\mathrm{1}+{x}}×{dx} \\ $$$${t}={ln}\left(\mathrm{1}+{x}\right)\:\:\:{dt}=\frac{{dx}}{\mathrm{1}+{x}}\: \\ $$$$\int_{\mathrm{0}} ^{{ln}\mathrm{2}} {tdt} \\ $$$$=\mid\frac{{t}^{\mathrm{2}} }{\mathrm{2}}\mid_{\mathrm{0}} ^{{ln}\mathrm{2}} \\ $$$$=\frac{\left({ln}\mathrm{2}\right)^{\mathrm{2}} }{\mathrm{2}} \\ $$
Commented by prof Abdo imad last updated on 22/May/18
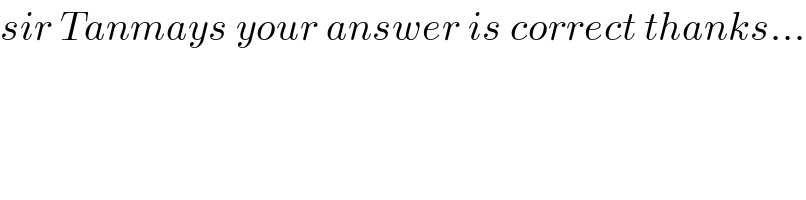
$${sir}\:{Tanmays}\:{your}\:{answer}\:{is}\:{correct}\:{thanks}… \\ $$
