Question Number 57103 by turbo msup by abdo last updated on 30/Mar/19
![let A_n =∫∫_w_n e^(−x^2 −y^2 ) (√(x^2 +y^2 ))dxdy with w_n =[(1/n),n]×[(1/n),n] 1) calculate A_n interms of n 2) find lim_(n→+∞) A_n](https://www.tinkutara.com/question/Q57103.png)
$${let}\:{A}_{{n}} =\int\int_{{w}_{{n}} } \:{e}^{−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} } \:\sqrt{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} }{dxdy} \\ $$$${with}\:{w}_{{n}} =\left[\frac{\mathrm{1}}{{n}},{n}\right]×\left[\frac{\mathrm{1}}{{n}},{n}\right] \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:{A}_{{n}} {interms}\:{of}\:{n} \\ $$$$\left.\mathrm{2}\right)\:{find}\:{lim}_{{n}\rightarrow+\infty} \:{A}_{{n}} \\ $$
Commented by 121194 last updated on 30/Mar/19
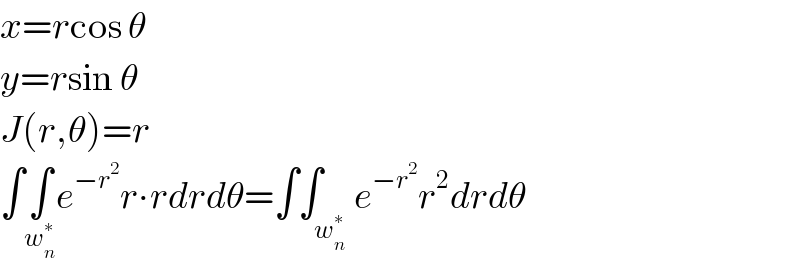
$${x}={r}\mathrm{cos}\:\theta \\ $$$${y}={r}\mathrm{sin}\:\theta \\ $$$${J}\left({r},\theta\right)={r} \\ $$$$\int\underset{{w}_{{n}} ^{\ast} } {\int}{e}^{−{r}^{\mathrm{2}} } {r}\centerdot{rdrd}\theta=\int\int_{{w}_{{n}} ^{\ast} } {e}^{−{r}^{\mathrm{2}} } {r}^{\mathrm{2}} {drd}\theta \\ $$
Commented by maxmathsup by imad last updated on 30/Mar/19
![let use the changement x=rcosθ and y=rsinθ we have (1/n)≤x≤n and (1/n) ≤y≤n ⇒(2/n^2 ) ≤x^2 +y^2 ≤2n^2 ⇒(2/n^2 ) ≤r^2 ≤2n^2 ⇒((√2)/n) ≤r≤n(√2) also we have x≥0 and y ≥0 ⇒ 0≤θ ≤(π/2) ⇒ A_n =∫∫_(((√2)/n)≤r≤n(√2)and 0≤θ≤(π/2)) e^(−r^2 ) r rdrdθ =∫∫_(w^′ n) r^2 e^(−r^2 ) drdθ =(∫_((√2)/n) ^(n(√2)) r^2 e^(−r^2 ) dr)∫_0 ^(π/2) dθ =(π/2) ∫_((√2)/n) ^(n(√2)) r^2 e^(−r^2 ) dr by parts u=r and v^′ =r e^(−r^2 ) ∫_((√2)/n) ^(n(√2)) r(r e^(−r^2 ) )dr =[−(1/2) r e^(−r^2 ) ]_((√2)/n) ^(n(√2)) +(1/2) ∫_((√2)/n) ^(n(√2)) e^(−r^2 ) dr =(1/2){((√2)/n) e^(−(2/n^2 )) −n(√2)e^(−2n^2 ) } +(1/2) ∫_((√2)/n) ^(n(√2)) e^(−r^2 ) dr ⇒ A_n =((π(√2))/4){ (1/n) e^(−(2/n^2 )) −n e^(−2n^2 ) } +(π/4) ∫_((√2)/n) ^(n(√2)) e^(−r^2 ) dr... 2) we have lim_(n→+∞) (1/n) e^(−(2/n^2 )) −n e^(−2n^2 ) =0 and lim_(n→+∞) ∫_((√2)/n) ^(n(√2)) e^(−r^2 ) dr =∫_0 ^∞ e^(−r^2 ) dr =((√π)/2) ⇒ lim_(n→+∞) A_n =((π(√π))/8) .](https://www.tinkutara.com/question/Q57123.png)
$${let}\:{use}\:{the}\:{changement}\:\:{x}={rcos}\theta\:{and}\:{y}={rsin}\theta\:\:{we}\:{have} \\ $$$$\frac{\mathrm{1}}{{n}}\leqslant{x}\leqslant{n}\:{and}\:\frac{\mathrm{1}}{{n}}\:\leqslant{y}\leqslant{n}\:\Rightarrow\frac{\mathrm{2}}{{n}^{\mathrm{2}} }\:\leqslant{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \:\leqslant\mathrm{2}{n}^{\mathrm{2}} \:\Rightarrow\frac{\mathrm{2}}{{n}^{\mathrm{2}} }\:\leqslant{r}^{\mathrm{2}} \:\leqslant\mathrm{2}{n}^{\mathrm{2}} \:\Rightarrow\frac{\sqrt{\mathrm{2}}}{{n}}\:\leqslant{r}\leqslant{n}\sqrt{\mathrm{2}} \\ $$$${also}\:{we}\:{have}\:{x}\geqslant\mathrm{0}\:{and}\:{y}\:\geqslant\mathrm{0}\:\Rightarrow\:\mathrm{0}\leqslant\theta\:\leqslant\frac{\pi}{\mathrm{2}}\:\Rightarrow \\ $$$${A}_{{n}} =\int\int_{\frac{\sqrt{\mathrm{2}}}{{n}}\leqslant{r}\leqslant{n}\sqrt{\mathrm{2}}{and}\:\mathrm{0}\leqslant\theta\leqslant\frac{\pi}{\mathrm{2}}} \:\:\:{e}^{−{r}^{\mathrm{2}} } \:{r}\:{rdrd}\theta\:=\int\int_{{w}^{'} {n}} {r}^{\mathrm{2}} \:{e}^{−{r}^{\mathrm{2}} } {drd}\theta \\ $$$$=\left(\int_{\frac{\sqrt{\mathrm{2}}}{{n}}} ^{{n}\sqrt{\mathrm{2}}} \:\:{r}^{\mathrm{2}} \:{e}^{−{r}^{\mathrm{2}} } {dr}\right)\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{d}\theta\:=\frac{\pi}{\mathrm{2}}\:\int_{\frac{\sqrt{\mathrm{2}}}{{n}}} ^{{n}\sqrt{\mathrm{2}}} \:{r}^{\mathrm{2}} \:{e}^{−{r}^{\mathrm{2}} } {dr}\:\:\:{by}\:{parts}\:{u}={r}\:{and}\:{v}^{'} \:={r}\:{e}^{−{r}^{\mathrm{2}} } \\ $$$$\int_{\frac{\sqrt{\mathrm{2}}}{{n}}} ^{{n}\sqrt{\mathrm{2}}} \:{r}\left({r}\:{e}^{−{r}^{\mathrm{2}} } \right){dr}\:=\left[−\frac{\mathrm{1}}{\mathrm{2}}\:{r}\:{e}^{−{r}^{\mathrm{2}} } \right]_{\frac{\sqrt{\mathrm{2}}}{{n}}} ^{{n}\sqrt{\mathrm{2}}} +\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\frac{\sqrt{\mathrm{2}}}{{n}}} ^{{n}\sqrt{\mathrm{2}}} \:{e}^{−{r}^{\mathrm{2}} } {dr} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{\sqrt{\mathrm{2}}}{{n}}\:{e}^{−\frac{\mathrm{2}}{{n}^{\mathrm{2}} }} \:\:\:−{n}\sqrt{\mathrm{2}}{e}^{−\mathrm{2}{n}^{\mathrm{2}} } \right\}\:+\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\frac{\sqrt{\mathrm{2}}}{{n}}} ^{{n}\sqrt{\mathrm{2}}} {e}^{−{r}^{\mathrm{2}} } {dr}\:\Rightarrow \\ $$$${A}_{{n}} =\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{4}}\left\{\:\:\frac{\mathrm{1}}{{n}}\:{e}^{−\frac{\mathrm{2}}{{n}^{\mathrm{2}} }} \:\:−{n}\:{e}^{−\mathrm{2}{n}^{\mathrm{2}} } \right\}\:+\frac{\pi}{\mathrm{4}}\:\int_{\frac{\sqrt{\mathrm{2}}}{{n}}} ^{{n}\sqrt{\mathrm{2}}} \:\:{e}^{−{r}^{\mathrm{2}} } {dr}… \\ $$$$\left.\mathrm{2}\right)\:{we}\:{have}\:{lim}_{{n}\rightarrow+\infty} \:\:\:\frac{\mathrm{1}}{{n}}\:{e}^{−\frac{\mathrm{2}}{{n}^{\mathrm{2}} }} \:\:−{n}\:{e}^{−\mathrm{2}{n}^{\mathrm{2}} } \:=\mathrm{0}\:\:{and}\:{lim}_{{n}\rightarrow+\infty} \:\:\int_{\frac{\sqrt{\mathrm{2}}}{{n}}} ^{{n}\sqrt{\mathrm{2}}} \:{e}^{−{r}^{\mathrm{2}} } {dr} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{r}^{\mathrm{2}} } {dr}\:=\frac{\sqrt{\pi}}{\mathrm{2}}\:\Rightarrow\:{lim}_{{n}\rightarrow+\infty} \:{A}_{{n}} =\frac{\pi\sqrt{\pi}}{\mathrm{8}}\:. \\ $$
