let-A-n-W-n-e-xy-x-2-y-2-dxdy-with-W-n-1-n-n-1-n-n-1-find-A-n-interms-of-n-2-determine-lim-n-A-n-

Question Number 56938 by maxmathsup by imad last updated on 26/Mar/19

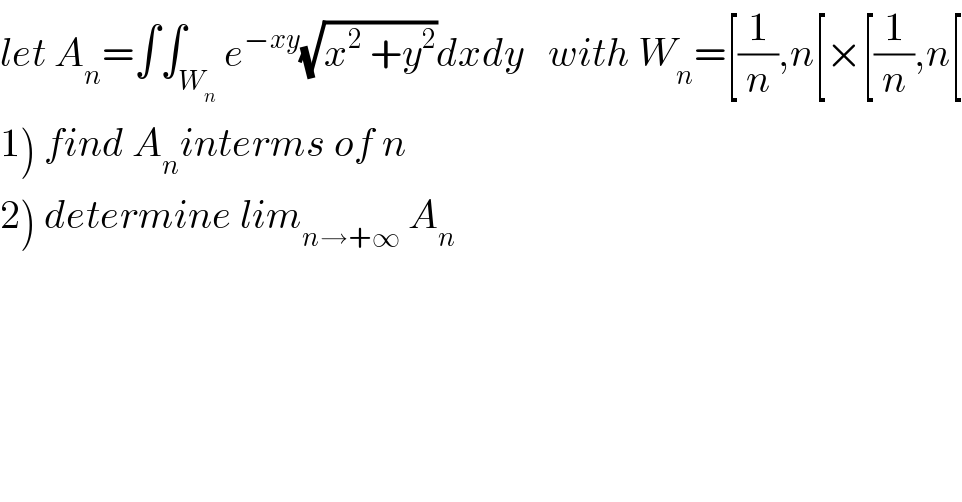
l e t A_{n} = \int \int_{W_{n}} e^{- x y} \sqrt{x^{2} + y^{2}} d x d y w i t h W_{n} = [\frac{1}{n}, n [\times [\frac{1}{n}, n [

1) f i n d A_{n} i n t e r m s o f n

2) d e t e r m i n e {l i m}_{n \to + \infty} A_{n}