Question Number 65198 by kaivan.ahmadi last updated on 26/Jul/19
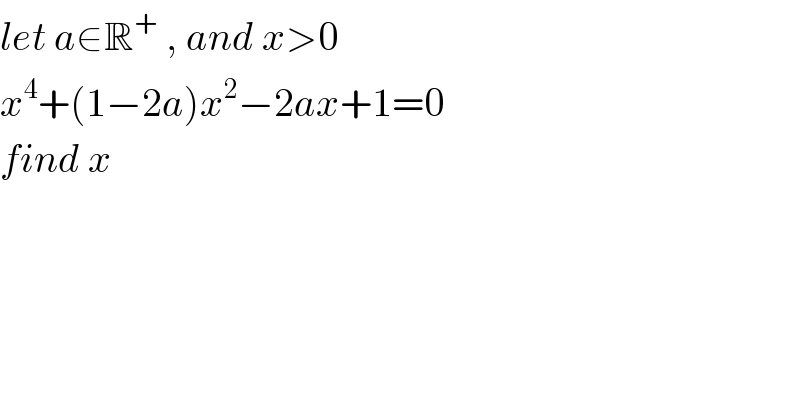
$${let}\:{a}\in\mathbb{R}^{+} \:,\:{and}\:{x}>\mathrm{0} \\ $$$${x}^{\mathrm{4}} +\left(\mathrm{1}−\mathrm{2}{a}\right){x}^{\mathrm{2}} −\mathrm{2}{ax}+\mathrm{1}=\mathrm{0} \\ $$$${find}\:{x} \\ $$
Commented by MJS last updated on 26/Jul/19

$$\mathrm{no}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{but}\:\mathrm{Ferrari}'\mathrm{s}\:\mathrm{formula} \\ $$$$\mathrm{which}\:\mathrm{is}\:\mathrm{super}\:\mathrm{complicated} \\ $$
Commented by kaivan.ahmadi last updated on 27/Jul/19
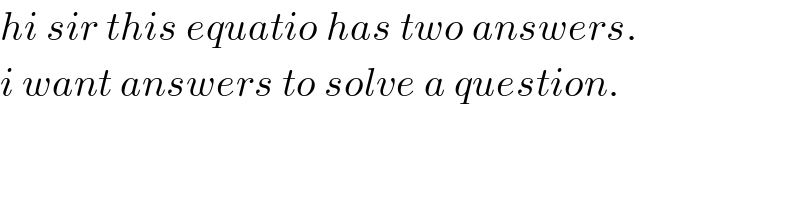
$${hi}\:{sir}\:{this}\:{equatio}\:{has}\:{two}\:{answers}. \\ $$$${i}\:{want}\:{answers}\:{to}\:{solve}\:{a}\:{question}. \\ $$
Commented by MJS last updated on 31/Jul/19
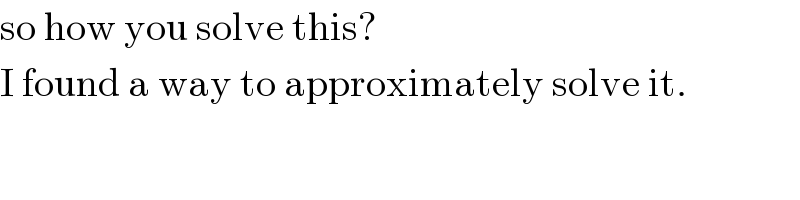
$$\mathrm{so}\:\mathrm{how}\:\mathrm{you}\:\mathrm{solve}\:\mathrm{this}? \\ $$$$\mathrm{I}\:\mathrm{found}\:\mathrm{a}\:\mathrm{way}\:\mathrm{to}\:\mathrm{approximately}\:\mathrm{solve}\:\mathrm{it}. \\ $$
Commented by kaivan.ahmadi last updated on 04/Aug/19

$${i}\:{dont}\:{know}\:{sir} \\ $$
Commented by MJS last updated on 04/Aug/19

$$\mathrm{look}\:\mathrm{at}\:\mathrm{question}\:\mathrm{65569} \\ $$
