Question Number 127452 by snipers237 last updated on 29/Dec/20
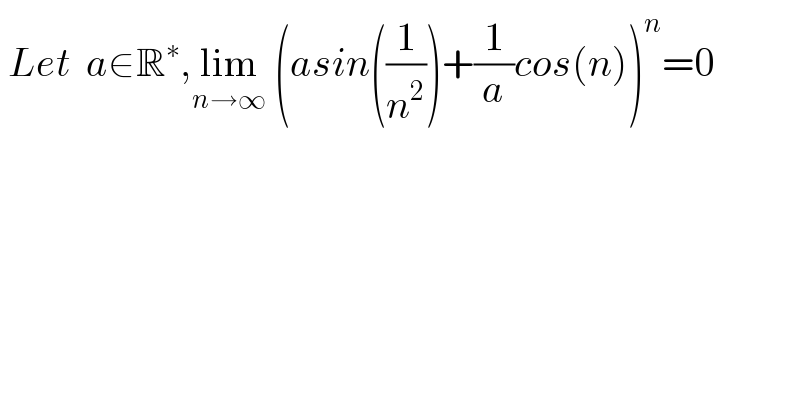
$$\:{Let}\:\:{a}\in\mathbb{R}^{\ast} ,\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\left({asin}\left(\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)+\frac{\mathrm{1}}{{a}}{cos}\left({n}\right)\right)^{{n}} =\mathrm{0} \\ $$
Answered by Ar Brandon last updated on 29/Dec/20
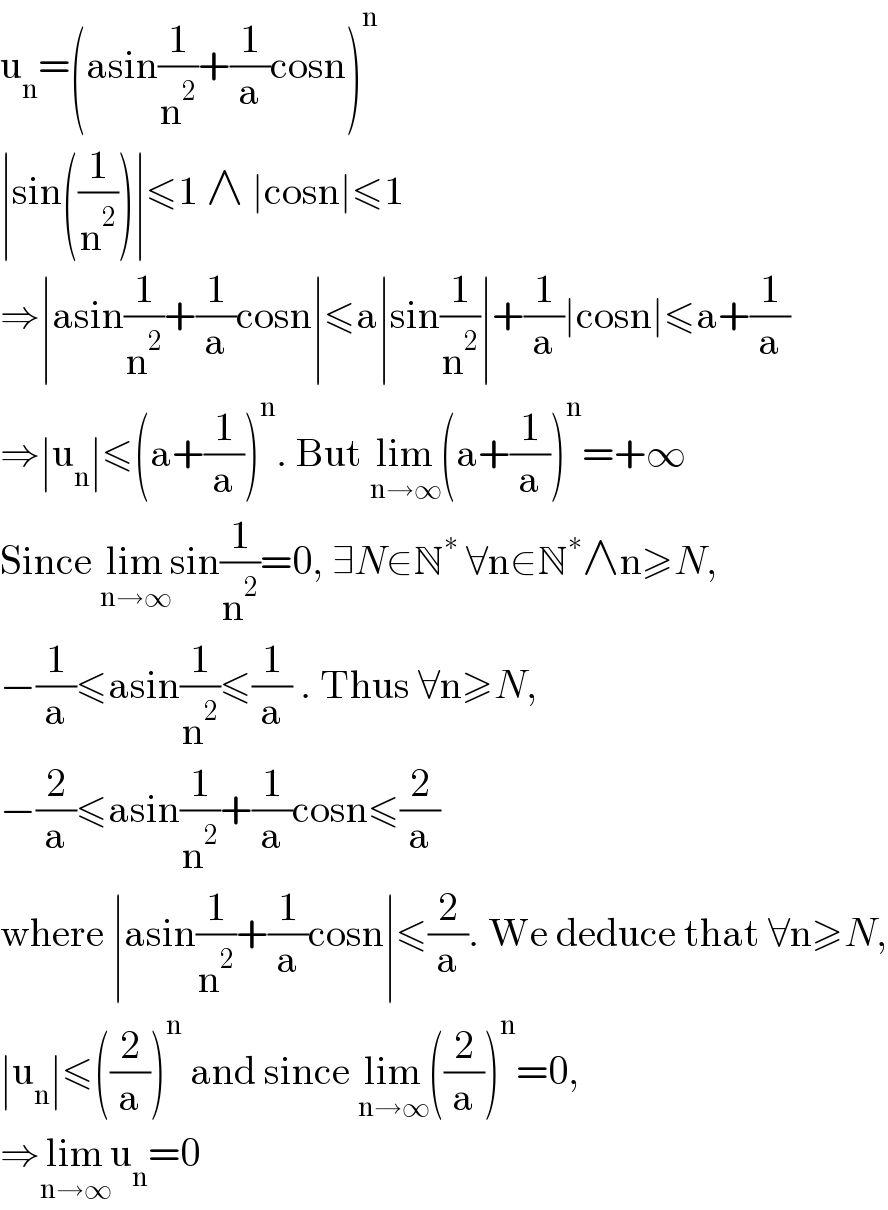
$$\mathrm{u}_{\mathrm{n}} =\left(\mathrm{asin}\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{a}}\mathrm{cosn}\right)^{\mathrm{n}} \\ $$$$\mid\mathrm{sin}\left(\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\right)\mid\leqslant\mathrm{1}\:\wedge\:\mid\mathrm{cosn}\mid\leqslant\mathrm{1} \\ $$$$\Rightarrow\mid\mathrm{asin}\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{a}}\mathrm{cosn}\mid\leqslant\mathrm{a}\mid\mathrm{sin}\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\mid+\frac{\mathrm{1}}{\mathrm{a}}\mid\mathrm{cosn}\mid\leqslant\mathrm{a}+\frac{\mathrm{1}}{\mathrm{a}}\: \\ $$$$\Rightarrow\mid\mathrm{u}_{\mathrm{n}} \mid\leqslant\left(\mathrm{a}+\frac{\mathrm{1}}{\mathrm{a}}\right)^{\mathrm{n}} .\:\mathrm{But}\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{a}+\frac{\mathrm{1}}{\mathrm{a}}\right)^{\mathrm{n}} =+\infty \\ $$$$\mathrm{Since}\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}sin}\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }=\mathrm{0},\:\exists{N}\in\mathbb{N}^{\ast} \:\forall\mathrm{n}\in\mathbb{N}^{\ast} \wedge\mathrm{n}\geqslant{N}, \\ $$$$−\frac{\mathrm{1}}{\mathrm{a}}\leqslant\mathrm{asin}\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\leqslant\frac{\mathrm{1}}{\mathrm{a}}\:.\:\mathrm{Thus}\:\forall\mathrm{n}\geqslant{N}, \\ $$$$−\frac{\mathrm{2}}{\mathrm{a}}\leqslant\mathrm{asin}\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{a}}\mathrm{cosn}\leqslant\frac{\mathrm{2}}{\mathrm{a}} \\ $$$$\mathrm{where}\:\mid\mathrm{asin}\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{a}}\mathrm{cosn}\mid\leqslant\frac{\mathrm{2}}{\mathrm{a}}.\:\mathrm{We}\:\mathrm{deduce}\:\mathrm{that}\:\forall\mathrm{n}\geqslant{N}, \\ $$$$\mid\mathrm{u}_{\mathrm{n}} \mid\leqslant\left(\frac{\mathrm{2}}{\mathrm{a}}\right)^{\mathrm{n}} \:\mathrm{and}\:\mathrm{since}\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{2}}{\mathrm{a}}\right)^{\mathrm{n}} =\mathrm{0}, \\ $$$$\Rightarrow\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}u}_{\mathrm{n}} =\mathrm{0} \\ $$
