Question Number 14809 by Tinkutara last updated on 04/Jun/17

$$\mathrm{Let}\:{ABC}\:\mathrm{be}\:\mathrm{an}\:\mathrm{acute}\:\mathrm{triangle}.\:\mathrm{Find} \\ $$$$\mathrm{the}\:\mathrm{positions}\:\mathrm{of}\:\mathrm{the}\:\mathrm{points}\:{M},\:{N},\:{P}\:\mathrm{on} \\ $$$$\mathrm{the}\:\mathrm{sides}\:{BC},\:{CA},\:{AB},\:\mathrm{respectively}, \\ $$$$\mathrm{such}\:\mathrm{that}\:\mathrm{the}\:\mathrm{perimeter}\:\mathrm{of}\:\mathrm{the}\:\mathrm{triangle} \\ $$$${MNP}\:\mathrm{is}\:\mathrm{minimal}. \\ $$
Commented by RasheedSoomro last updated on 04/Jun/17
$$\mathrm{I}\:\mathrm{think}\:\mathrm{they}\:\mathrm{are}\:\mathrm{midpoints}\:\mathrm{of}\:\mathrm{the}\:\mathrm{sides}. \\ $$
Commented by Tinkutara last updated on 04/Jun/17

$$\mathrm{No}\:\mathrm{it}\:\mathrm{is}\:\mathrm{another}\:\mathrm{condition}. \\ $$
Answered by mrW1 last updated on 05/Jun/17

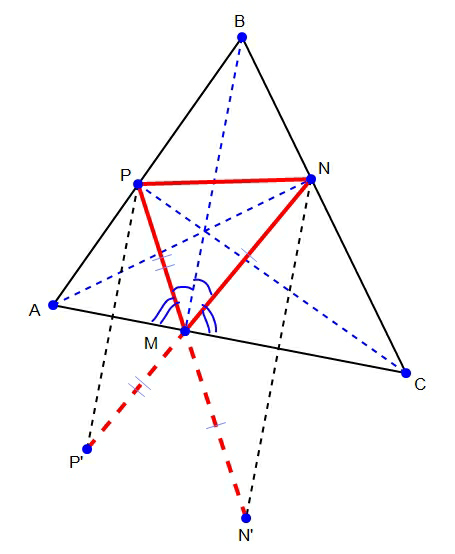
$${Let}\:{us}\:{consider}\:{if}\:{the}\:{points}\:{N}\:{and}\:{P} \\ $$$${are}\:{given},\:{how}\:{we}\:{determine}\:{the}\:{point} \\ $$$${M}\:{so}\:{that}\:{the}\:{length}\:{NM}+{MP}\:{is} \\ $$$${minimal}. \\ $$$$ \\ $$$${Let}\:{P}'\:{and}\:{N}'\:{the}\:{mirror}\:{points}\:{of} \\ $$$${P}\:{and}\:{N}\:{about}\:{AC}.\:{We}\:{know}\:{PM}+{MN} \\ $$$${is}\:{minimal}\:{if}\:{M}\:{is}\:{the}\:{intersection} \\ $$$${point}\:{from}\:{NP}'\:{with}\:{AC}\:{or}\:{PN}'\:{with} \\ $$$${AC}.\:{In}\:{this}\:{case}\:{PM}\:{and}\:{MN}\:{behavior} \\ $$$${like}\:{a}\:{light}\:{ray}\:{which}\:{is}\:{reflected}\:{by} \\ $$$${a}\:{mirror}\:{AC}. \\ $$$${As}\:{result}\:{BM}\bot{AC}. \\ $$$${See}\:{diagram}. \\ $$$$ \\ $$$${Due}\:{to}\:{symmetry}\:{we}\:{can}\:{see}\:{that} \\ $$$${the}\:{perimeter}\:{of}\:\Delta{MNP}\:{is}\:{minimal} \\ $$$${M},{N},{P}\:{are}\:{the}\:{feet}\:{of}\:{the}\:{altitudes} \\ $$$${of}\:\Delta{ABC}. \\ $$
Commented by mrW1 last updated on 04/Jun/17
Commented by Tinkutara last updated on 05/Jun/17
$$\mathrm{Answer}:\:\mathrm{When}\:{M},\:{N}\:\mathrm{and}\:{P}\:\mathrm{are}\:\mathrm{the}\:\mathrm{feet} \\ $$$$\mathrm{of}\:\mathrm{altitudes}\:\mathrm{of}\:\mathrm{the}\:\Delta{ABC}. \\ $$$$\mathrm{How}? \\ $$
Commented by mrW1 last updated on 05/Jun/17

$${Your}\:{answer}\:{is}\:{right}\:{sir}.\:{I}\:{came}\:{also} \\ $$$${to}\:{this}\:{conclussion}\:{and}\:{have}\:{fixed} \\ $$$${my}\:{working}\:{above}. \\ $$
Commented by ajfour last updated on 05/Jun/17
$${wont}\:\bigtriangleup{MNP}\:\:{be}\:{equilateral}\:{with} \\ $$$${such}\:{condition}. \\ $$
Commented by Tinkutara last updated on 05/Jun/17

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$
Commented by mrW1 last updated on 05/Jun/17
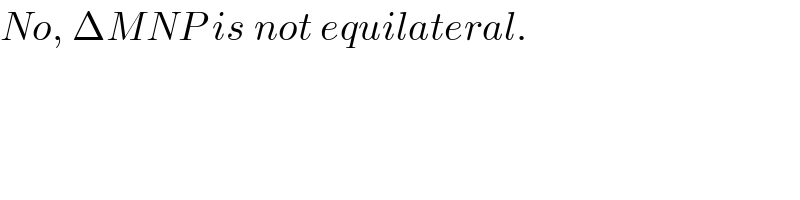
$${No},\:\Delta{MNP}\:{is}\:{not}\:{equilateral}. \\ $$
