Question Number 16066 by Tinkutara last updated on 21/Jun/17
![Let ABCD be a convex quadrilateral and let k > 0 be a real number. Find the locus of points M in its interior such that [MAB] + 2[MCD] = k.](https://www.tinkutara.com/question/Q16066.png)
$$\mathrm{Let}\:{ABCD}\:\mathrm{be}\:\mathrm{a}\:\mathrm{convex}\:\mathrm{quadrilateral} \\ $$$$\mathrm{and}\:\mathrm{let}\:{k}\:>\:\mathrm{0}\:\mathrm{be}\:\mathrm{a}\:\mathrm{real}\:\mathrm{number}.\:\mathrm{Find} \\ $$$$\mathrm{the}\:\mathrm{locus}\:\mathrm{of}\:\mathrm{points}\:{M}\:\mathrm{in}\:\mathrm{its}\:\mathrm{interior} \\ $$$$\mathrm{such}\:\mathrm{that} \\ $$$$\left[{MAB}\right]\:+\:\mathrm{2}\left[{MCD}\right]\:=\:{k}. \\ $$
Answered by mrW1 last updated on 28/Jun/17
![Let AB=a, CD=b ⇒[MAB]=(1/2)ah_1 ⇒[MCD]=(1/2)bh_2 with h_1 =distance from M to side AB h_2 =distance from M to side CD [MAB] + 2[MCD] = k=constant ⇒(1/2)(ah_1 +2bh_2 )=k ⇒(1/2)(ah_1 +b′h_2 )=k with b′=2b](https://www.tinkutara.com/question/Q16943.png)
$$\mathrm{Let}\:\mathrm{AB}=\mathrm{a},\:\mathrm{CD}=\mathrm{b} \\ $$$$\Rightarrow\left[\mathrm{MAB}\right]=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ah}_{\mathrm{1}} \\ $$$$\Rightarrow\left[\mathrm{MCD}\right]=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{bh}_{\mathrm{2}} \\ $$$$\mathrm{with} \\ $$$$\mathrm{h}_{\mathrm{1}} =\mathrm{distance}\:\mathrm{from}\:\mathrm{M}\:\mathrm{to}\:\mathrm{side}\:\mathrm{AB} \\ $$$$\mathrm{h}_{\mathrm{2}} =\mathrm{distance}\:\mathrm{from}\:\mathrm{M}\:\mathrm{to}\:\mathrm{side}\:\mathrm{CD} \\ $$$$ \\ $$$$\left[{MAB}\right]\:+\:\mathrm{2}\left[{MCD}\right]\:=\:{k}=\mathrm{constant} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{ah}_{\mathrm{1}} +\mathrm{2bh}_{\mathrm{2}} \right)=\mathrm{k} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{ah}_{\mathrm{1}} +\mathrm{b}'\mathrm{h}_{\mathrm{2}} \right)=\mathrm{k}\:\mathrm{with}\:\mathrm{b}'=\mathrm{2b} \\ $$
Commented by mrW1 last updated on 28/Jun/17
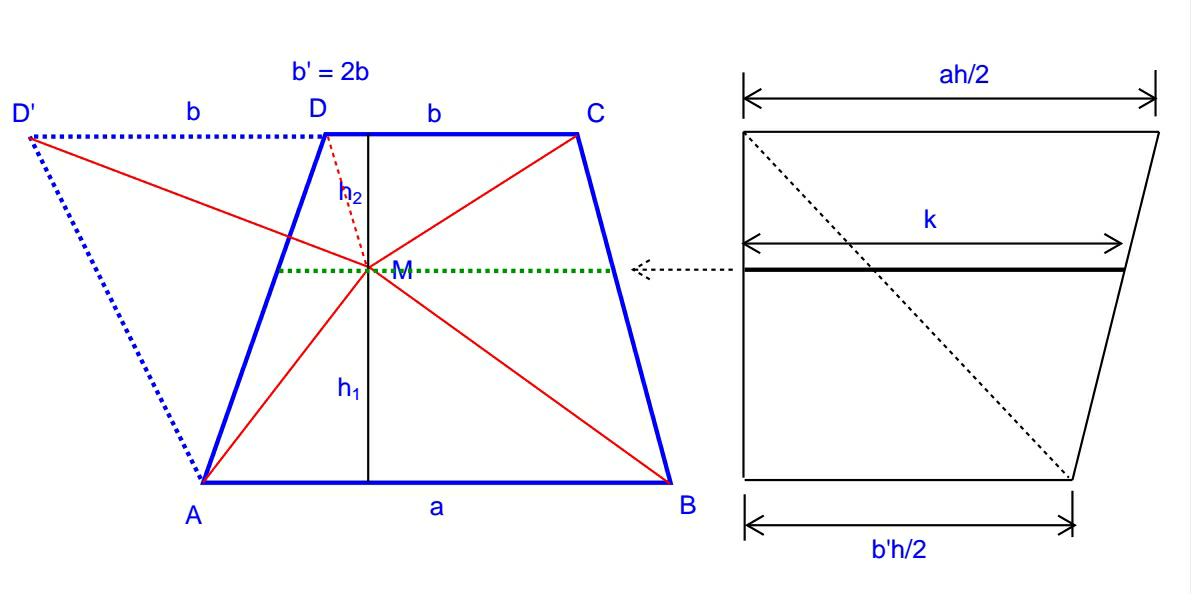
Commented by mrW1 last updated on 29/Jun/17
![Case 1: AB//CD h_1 +h_2 =h=constant (1/2)(ah_1 +b′h_2 )=k ⇒(1/2)[ah_1 +b′(h−h_1 )]=k ⇒(a−b′)h_1 +b′h=2k if a=b′: ⇒ b′h=2k ⇒ k=((b′h)/2)=((ah)/2) i.e. k must be ((ah)/2), otherwise there is no solution. In this situation M can be everywhere in interior of ABCD. if a≠b′: (a−b′)h_1 +b′h=2k ⇒h_1 =((2k−b′h)/(a−b′))=((k/((b′h)/2))−1)×((1/((a/(b′))−1)))×h=constant ⇒the locus of M is a straight line parallel to AB and CD. But there is a solution only if the value of k is between ((ah)/2) and ((b′h)/2), see diagram above. When k=((ah)/2), M lies on side CD. When k=((b′h)/2), M lies on side AB.](https://www.tinkutara.com/question/Q16949.png)
$$\mathrm{Case}\:\mathrm{1}:\:\mathrm{AB}//\mathrm{CD} \\ $$$$\mathrm{h}_{\mathrm{1}} +\mathrm{h}_{\mathrm{2}} =\mathrm{h}=\mathrm{constant} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{ah}_{\mathrm{1}} +\mathrm{b}'\mathrm{h}_{\mathrm{2}} \right)=\mathrm{k} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{ah}_{\mathrm{1}} +\mathrm{b}'\left(\mathrm{h}−\mathrm{h}_{\mathrm{1}} \right)\right]=\mathrm{k} \\ $$$$\Rightarrow\left(\mathrm{a}−\mathrm{b}'\right)\mathrm{h}_{\mathrm{1}} +\mathrm{b}'\mathrm{h}=\mathrm{2k} \\ $$$$ \\ $$$$\mathrm{if}\:\mathrm{a}=\mathrm{b}': \\ $$$$\Rightarrow\:\mathrm{b}'\mathrm{h}=\mathrm{2k}\:\Rightarrow\:\mathrm{k}=\frac{\mathrm{b}'\mathrm{h}}{\mathrm{2}}=\frac{\mathrm{ah}}{\mathrm{2}} \\ $$$$\mathrm{i}.\mathrm{e}.\:\mathrm{k}\:\mathrm{must}\:\mathrm{be}\:\frac{\mathrm{ah}}{\mathrm{2}},\:\mathrm{otherwise}\:\mathrm{there}\:\mathrm{is} \\ $$$$\mathrm{no}\:\mathrm{solution}.\:\mathrm{In}\:\mathrm{this}\:\mathrm{situation}\:\mathrm{M}\:\mathrm{can} \\ $$$$\mathrm{be}\:\mathrm{everywhere}\:\mathrm{in}\:\mathrm{interior}\:\mathrm{of}\:\mathrm{ABCD}. \\ $$$$ \\ $$$$\mathrm{if}\:\mathrm{a}\neq\mathrm{b}': \\ $$$$\left(\mathrm{a}−\mathrm{b}'\right)\mathrm{h}_{\mathrm{1}} +\mathrm{b}'\mathrm{h}=\mathrm{2k} \\ $$$$\Rightarrow\mathrm{h}_{\mathrm{1}} =\frac{\mathrm{2k}−\mathrm{b}'\mathrm{h}}{\mathrm{a}−\mathrm{b}'}=\left(\frac{\mathrm{k}}{\frac{\mathrm{b}'\mathrm{h}}{\mathrm{2}}}−\mathrm{1}\right)×\left(\frac{\mathrm{1}}{\frac{\mathrm{a}}{\mathrm{b}'}−\mathrm{1}}\right)×\mathrm{h}=\mathrm{constant} \\ $$$$\Rightarrow\mathrm{the}\:\mathrm{locus}\:\mathrm{of}\:\mathrm{M}\:\mathrm{is}\:\mathrm{a}\:\mathrm{straight}\:\mathrm{line} \\ $$$$\mathrm{parallel}\:\mathrm{to}\:\mathrm{AB}\:\mathrm{and}\:\mathrm{CD}.\:\mathrm{But}\:\mathrm{there} \\ $$$$\mathrm{is}\:\mathrm{a}\:\mathrm{solution}\:\mathrm{only}\:\mathrm{if}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{k}\:\mathrm{is} \\ $$$$\mathrm{between}\:\frac{\mathrm{ah}}{\mathrm{2}}\:\mathrm{and}\:\frac{\mathrm{b}'\mathrm{h}}{\mathrm{2}},\:\mathrm{see}\:\mathrm{diagram}\:\mathrm{above}. \\ $$$$\mathrm{When}\:\mathrm{k}=\frac{\mathrm{ah}}{\mathrm{2}},\:\mathrm{M}\:\mathrm{lies}\:\mathrm{on}\:\mathrm{side}\:\mathrm{CD}. \\ $$$$\mathrm{When}\:\mathrm{k}=\frac{\mathrm{b}'\mathrm{h}}{\mathrm{2}},\:\mathrm{M}\:\mathrm{lies}\:\mathrm{on}\:\mathrm{side}\:\mathrm{AB}. \\ $$
Commented by mrW1 last updated on 29/Jun/17
$$\mathrm{Case}\:\mathrm{2}:\:\mathrm{AB}\:\mathrm{and}\:\mathrm{CD}\:\mathrm{meets}\:\mathrm{at}\:\mathrm{O} \\ $$$$\angle\mathrm{AOD}=\alpha \\ $$$$ \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{ah}_{\mathrm{1}} +\mathrm{b}'\mathrm{h}_{\mathrm{2}} \right)=\mathrm{k} \\ $$$$\Rightarrow\:\mathrm{ah}_{\mathrm{1}} +\mathrm{b}'\mathrm{h}_{\mathrm{2}} =\mathrm{2k} \\ $$$$\mathrm{that}\:\mathrm{means}\:\mathrm{point}\:\mathrm{M}\:\mathrm{has}\:\mathrm{to}\:\mathrm{fulfill}\:\mathrm{that} \\ $$$$\mathrm{ah}_{\mathrm{1}} +\mathrm{b}'\mathrm{h}_{\mathrm{2}} =\mathrm{constant}\:\mathrm{which}\:\mathrm{is}\:\mathrm{2k}. \\ $$$$ \\ $$$$\mathrm{We}\:\mathrm{make}\:\mathrm{OA}'=\mathrm{AB}=\mathrm{a}\:\mathrm{and} \\ $$$$\mathrm{OD}'=\mathrm{2CD}=\mathrm{2b}=\mathrm{b}'. \\ $$$$ \\ $$$$\mathrm{We}\:\mathrm{get}\:\mathrm{A}'\mathrm{D}'. \\ $$$$\mathrm{Every}\:\mathrm{point}\:\mathrm{on}\:\mathrm{A}'\mathrm{D}'\:\mathrm{fulfills}\:\mathrm{that}\: \\ $$$$\mathrm{ah}_{\mathrm{1}} +\mathrm{b}'\mathrm{h}_{\mathrm{2}} =\mathrm{constant}. \\ $$$$\mathrm{Every}\:\mathrm{point}\:\mathrm{on}\:\mathrm{any}\:\mathrm{straight}\:\mathrm{line}\://\:\mathrm{A}'\mathrm{D}' \\ $$$$\mathrm{fulfills}\:\mathrm{also}\:\mathrm{this}\:\mathrm{condition}. \\ $$$$ \\ $$$$\mathrm{Each}\:\mathrm{line}\:\mathrm{parallel}\:\mathrm{to}\:\mathrm{A}'\mathrm{D}'\:\mathrm{stands}\:\mathrm{for} \\ $$$$\mathrm{a}\:\mathrm{certain}\:\mathrm{value}\:\mathrm{of}\:\mathrm{k}\:\mathrm{from}\:\mathrm{0}\:\mathrm{to}\:+\infty. \\ $$$$ \\ $$$$\mathrm{We}\:\mathrm{have}\:\mathrm{following}\:\mathrm{special}\:\mathrm{lines}\://\:\mathrm{A}'\mathrm{D}': \\ $$$$ \\ $$$$\mathrm{A1}\:\mathrm{corresponding}\:\mathrm{to}\:\mathrm{k}_{\mathrm{1}} =\mathrm{2A}_{\Delta\mathrm{ACD}} \\ $$$$\mathrm{D2}\:\mathrm{corresponding}\:\mathrm{to}\:\mathrm{k}_{\mathrm{2}} =\mathrm{A}_{\Delta\mathrm{ADB}} \\ $$$$\mathrm{C3}\:\mathrm{corresponding}\:\mathrm{to}\:\mathrm{k}_{\mathrm{3}} =\mathrm{A}_{\Delta\mathrm{ACB}} \\ $$$$\mathrm{B4}\:\mathrm{corresponding}\:\mathrm{to}\:\mathrm{k}_{\mathrm{4}} =\mathrm{2A}_{\Delta\mathrm{CBD}} \\ $$$$ \\ $$$$\mathrm{So}\:\mathrm{we}\:\mathrm{have}: \\ $$$$\mathrm{if}\:\mathrm{k}<\mathrm{k}_{\mathrm{1}} \:\Rightarrow\:\mathrm{no}\:\mathrm{solution}\:\mathrm{for}\:\mathrm{point}\:\mathrm{M} \\ $$$$ \\ $$$$\mathrm{if}\:\mathrm{k}_{\mathrm{1}} \leqslant\mathrm{k}\leqslant\mathrm{k}_{\mathrm{2}} \:\Rightarrow\:\mathrm{Locus}\:\mathrm{of}\:\mathrm{M}\:\mathrm{is}\:\mathrm{a}\:\mathrm{part}\:\mathrm{of}\:\mathrm{straight}\:\mathrm{line}\:\mathrm{from}\:\mathrm{AD}\:\mathrm{to}\:\mathrm{AB} \\ $$$$ \\ $$$$\mathrm{if}\:\mathrm{k}_{\mathrm{2}} \leqslant\mathrm{k}\leqslant\mathrm{k}_{\mathrm{3}} \:\Rightarrow\:\mathrm{Locus}\:\mathrm{of}\:\mathrm{M}\:\mathrm{is}\:\mathrm{a}\:\mathrm{straight}\:\mathrm{line}\:\mathrm{EF}\://\:\mathrm{A}'\mathrm{D}' \\ $$$$ \\ $$$$\mathrm{if}\:\mathrm{k}_{\mathrm{3}} \leqslant\mathrm{k}\leqslant\mathrm{k}_{\mathrm{4}} \:\Rightarrow\:\mathrm{Locus}\:\mathrm{of}\:\mathrm{M}\:\mathrm{is}\:\mathrm{a}\:\mathrm{part}\:\mathrm{of}\:\mathrm{straight}\:\mathrm{line}\:\mathrm{from}\:\mathrm{BC}\:\mathrm{to}\:\mathrm{AB} \\ $$$$ \\ $$$$\mathrm{if}\:\mathrm{k}>\mathrm{k}_{\mathrm{4}} \:\Rightarrow\:\mathrm{no}\:\mathrm{solution}\:\mathrm{for}\:\mathrm{point}\:\mathrm{M} \\ $$
Commented by Tinkutara last updated on 29/Jun/17
$$\mathrm{Thanks}\:\mathrm{Sir}!\:\boldsymbol{\mathrm{Very}}\:\boldsymbol{\mathrm{much}}. \\ $$
Commented by mrW1 last updated on 28/Jun/17
Commented by mrW1 last updated on 28/Jun/17
$$\mathrm{Here}\:\mathrm{is}\:\mathrm{how}\:\mathrm{to}\:\mathrm{determine}\:\mathrm{the}\:\mathrm{line}\:\mathrm{EF} \\ $$$$\mathrm{for}\:\mathrm{a}\:\mathrm{certain}\:\mathrm{value}\:\mathrm{of}\:\mathrm{k}. \\ $$$$ \\ $$$$\mathrm{Area}\:\mathrm{of}\:\Delta\mathrm{OA}'\mathrm{D}'=\mathrm{A}_{\mathrm{0}} \\ $$$$\mathrm{A}_{\mathrm{0}} =\mathrm{ab}'\mathrm{sin}\:\alpha \\ $$$$ \\ $$$$\mathrm{A}'\mathrm{D}'\:\mathrm{stands}\:\mathrm{for}\:\mathrm{k}=\mathrm{k}_{\mathrm{0}} =\mathrm{A}_{\mathrm{0}} \\ $$$$\mathrm{EF}\:\mathrm{stands}\:\mathrm{for}\:\mathrm{k} \\ $$$$ \\ $$$$\frac{\mathrm{OE}}{\mathrm{OA}'}=\sqrt{\frac{\mathrm{k}}{\mathrm{A}_{\mathrm{0}} }} \\ $$$$\Rightarrow\mathrm{OE}=\sqrt{\frac{\mathrm{k}}{\mathrm{A}_{\mathrm{0}} }\:}\mathrm{a} \\ $$
Answered by Tinkutara last updated on 29/Jun/17
$$\mathrm{Combining}\:\mathrm{Problems}\:\mathrm{3}\:\mathrm{and}\:\mathrm{5}\:\mathrm{and}\:\mathrm{using} \\ $$$$\mathrm{the}\:\mathrm{construction}\:\mathrm{above},\:\mathrm{we}\:\mathrm{deduce} \\ $$$$\mathrm{that}\:\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:{XY}\:'{M}\:\mathrm{is}\:\mathrm{constant}. \\ $$$$\left(\mathrm{Figure}\right).\:\mathrm{It}\:\mathrm{results}\:\mathrm{that}\:\mathrm{the}\:\mathrm{locus}\:\mathrm{is} \\ $$$$\left(\mathrm{according}\:\mathrm{to}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:{k}\right)\:\mathrm{either}\:\mathrm{a} \\ $$$$\mathrm{segment}\:{KL}\:\mathrm{parallel}\:\mathrm{to}\:{XY}\:',\:\mathrm{or}\:\mathrm{a} \\ $$$$\mathrm{point},\:\mathrm{or}\:\mathrm{the}\:\mathrm{empty}\:\mathrm{set}. \\ $$
Commented by Tinkutara last updated on 29/Jun/17
Commented by Tinkutara last updated on 29/Jun/17
$$\mathrm{This}\:\mathrm{is}\:\mathrm{my}\:\mathrm{book}'\mathrm{s}\:\mathrm{solution}.\:\mathrm{Here} \\ $$$$\mathrm{Problem}\:\mathrm{3}\:\mathrm{is}\:\mathrm{Q}.\:\mathrm{16064}\:\mathrm{and}\:\mathrm{5}\:\mathrm{is}\:\mathrm{Q}.\:\mathrm{16066} \\ $$$$\mathrm{problem}.\:\left(\mathrm{This}\:\mathrm{Question}\right) \\ $$
Commented by mrW1 last updated on 30/Jun/17
$$\mathrm{In}\:\mathrm{princip}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{the}\:\mathrm{same}\:\mathrm{as} \\ $$$$\mathrm{mine}.\:\mathrm{The}\:\mathrm{locus}\:\mathrm{of}\:\mathrm{M}\:\mathrm{is}\:\mathrm{KL}\:\mathrm{which}\:\mathrm{is} \\ $$$$\mathrm{parallel}\:\mathrm{to}\:\mathrm{XY}'\:\left(\mathrm{but}\:\mathrm{the}\:\mathrm{figure}\:\mathrm{shows}\right. \\ $$$$\left.\mathrm{KL}//\mathrm{XY},\:\mathrm{this}\:\mathrm{is}\:\mathrm{wrong}\right) \\ $$$$\mathrm{And}\:\mathrm{my}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{much}\:\mathrm{more}\:\mathrm{exact}, \\ $$$$\mathrm{it}\:\mathrm{tells}\:\mathrm{you}\:\mathrm{the}\:\mathrm{different}\:\mathrm{situations}\:\mathrm{for} \\ $$$$\mathrm{the}\:\mathrm{locus}\:\mathrm{of}\:\mathrm{M}\:\mathrm{depending}\:\mathrm{on}\:\mathrm{the}\:\mathrm{ranges}\:\mathrm{for} \\ $$$$\mathrm{k}:\:\mathrm{k}_{\mathrm{1}} \:\mathrm{till}\:\mathrm{t}_{\mathrm{4}} .\:\mathrm{My}\:\mathrm{answer}\:\mathrm{tells}\:\mathrm{also}\:\mathrm{how} \\ $$$$\mathrm{to}\:\mathrm{determine}\:\mathrm{the}\:\mathrm{position}\:\mathrm{of}\:\mathrm{locus}\:\mathrm{of} \\ $$$$\mathrm{M}\:\mathrm{for}\:\mathrm{a}\:\mathrm{certain}\:\mathrm{value}\:\mathrm{of}\:\mathrm{k}. \\ $$$$\mathrm{The}\:\mathrm{answer}\:\mathrm{of}\:\mathrm{book}\:\mathrm{mentions}\:\mathrm{only} \\ $$$$\mathrm{that}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{could}\:\mathrm{be}\:\mathrm{empty}\:\mathrm{set}, \\ $$$$\mathrm{but}\:\mathrm{not}\:\mathrm{when}.\:\mathrm{My}\:\mathrm{answer}\:\mathrm{tells}\:\mathrm{exactly} \\ $$$$\mathrm{when},\:\mathrm{i}.\mathrm{e}.\:\mathrm{if}\:\mathrm{k}<\mathrm{k}_{\mathrm{1}} \:\mathrm{or}\:\mathrm{k}>\mathrm{k}_{\mathrm{4}} \:\mathrm{and}\:\mathrm{gives} \\ $$$$\mathrm{the}\:\mathrm{values}\:\mathrm{of}\:\mathrm{k}_{\mathrm{1}} \:\mathrm{and}\:\mathrm{k}_{\mathrm{4}} \:\mathrm{as}\:\mathrm{well}\:\mathrm{as}\:\mathrm{other} \\ $$$$\mathrm{special}\:\mathrm{k}−\mathrm{values}\:\mathrm{k}_{\mathrm{2}} \:\mathrm{and}\:\mathrm{k}_{\mathrm{3}} \:\mathrm{when}\:\mathrm{the} \\ $$$$\mathrm{locus}\:\mathrm{of}\:\mathrm{M}\:\mathrm{is}\:\mathrm{a}\:\mathrm{single}\:\mathrm{point}\:\left(\mathrm{k}=\mathrm{k}_{\mathrm{1}} ,\mathrm{k}=\mathrm{k}_{\mathrm{4}} \right),\:\mathrm{part}\:\mathrm{of}\:\mathrm{a} \\ $$$$\mathrm{segment}\:\mathrm{from}\:\mathrm{AB}\:\mathrm{to}\:\mathrm{CD}\:\left(\mathrm{k}_{\mathrm{1}} <\mathrm{k}<\mathrm{k}_{\mathrm{2}} ,\:\mathrm{k}_{\mathrm{3}} <\mathrm{k}<\mathrm{k}_{\mathrm{4}} \:\right)\mathrm{or}\:\mathrm{a}\:\mathrm{whole} \\ $$$$\mathrm{segment}\:\mathrm{from}\:\mathrm{AB}\:\mathrm{to}\:\mathrm{CD}\:\left(\mathrm{k}_{\mathrm{2}} \leqslant\mathrm{k}\leqslant\mathrm{k}_{\mathrm{3}} \right). \\ $$$$ \\ $$$$\mathrm{But}\:\mathrm{the}\:\mathrm{core}\:\mathrm{of}\:\mathrm{both}\:\mathrm{solutions}\:\mathrm{is}\:\mathrm{the} \\ $$$$\mathrm{same}:\:\mathrm{the}\:\mathrm{locus}\:\mathrm{of}\:\mathrm{M}\:\mathrm{is}\:\mathrm{a}\:\mathrm{straight}\:\mathrm{line} \\ $$$$\mathrm{parallel}\:\mathrm{to}\:\mathrm{XY}'\:\left(=\mathrm{A}'\mathrm{D}'\:\mathrm{by}\:\mathrm{me}\right)\:\mathrm{with} \\ $$$$\mathrm{TX}=\mathrm{AB}\:\left(=\mathrm{OA}'\:\mathrm{by}\:\mathrm{me}\right)\:\mathrm{and} \\ $$$$\mathrm{TY}'=\mathrm{2CD}\:\left(=\mathrm{OD}'\:\mathrm{by}\:\mathrm{me}\right) \\ $$$$ \\ $$$$\mathrm{Certainly}\:\mathrm{my}\:\mathrm{answer}\:\mathrm{treats}\:\mathrm{also}\:\mathrm{the} \\ $$$$\mathrm{case}\:\mathrm{if}\:\mathrm{AB}//\mathrm{CD}. \\ $$
Commented by Tinkutara last updated on 30/Jun/17
$$\mathrm{Thanks}\:\mathrm{Sir}!\:\mathrm{I}\:\mathrm{knew}\:\mathrm{your}\:\mathrm{solution}\:\mathrm{was} \\ $$$$\mathrm{correct}.\:\mathrm{But}\:\mathrm{I}\:\mathrm{posted}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{in}\:\mathrm{my} \\ $$$$\mathrm{book}\:\mathrm{to}\:\mathrm{show}\:\mathrm{that}\:\mathrm{it}\:\mathrm{has}\:\mathrm{a}\:\mathrm{good} \\ $$$$\mathrm{collection}\:\mathrm{of}\:\mathrm{questions}\:\mathrm{but}\:\mathrm{not}\:\mathrm{solutions}. \\ $$
Commented by mrW1 last updated on 30/Jun/17
$$\mathrm{They}\:\mathrm{are}\:\mathrm{really}\:\mathrm{interesting}\:\mathrm{questions}. \\ $$