Let-AC-be-a-line-segment-in-the-plane-and-B-a-point-between-A-and-C-Construct-isosceles-triangles-PAB-and-QBC-on-one-side-of-the-segment-AC-such-that-APB-BQC-120-and-an-isosceles-triangle-RAC-

Question Number 19293 by Tinkutara last updated on 08/Aug/17

Let A C be a line segment in the plane

and B a point between A and C .

Construct isosceles triangles P A B and

Q B C on one side of the segment A C

such that ∠ A P B = ∠ B Q C = 120 ° and

an isosceles triangle R A C on the other

side of A C such that ∠ A R C = 120 ° .

Show that P Q R is an equilateral

triangle .

Commented by ajfour last updated on 08/Aug/17

Commented by ajfour last updated on 08/Aug/17

{PQ}^{2} = {(a + c)}^{2} + \frac{{(c - a)}^{2}}{3}

= \frac{4}{3} (a^{2} + c^{2} + ac)

{QR}^{2} = a^{2} + \frac{{(2 c + a)}^{2}}{3}

= \frac{4}{3} (a^{2} + c^{2} + ac)

{RP}^{2} = c^{2} + \frac{{(2 a + c)}^{2}}{3}

= \frac{4}{3} (a^{2} + c^{2} + ac)

\Rightarrow PQ = QR = RP, hence △ PQR

is equilateral .

Commented by Tinkutara last updated on 08/Aug/17

Thank you very much Sir!

Answered by Tinkutara last updated on 03/Dec/17

Commented by Tinkutara last updated on 03/Dec/17

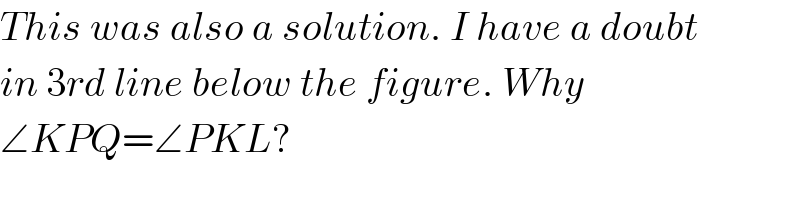
T h i s w a s a l s o a s o l u t i o n . I h a v e a d o u b t

i n 3 r d l i n e b e l o w t h e f i g u r e . W h y

∠ K P Q = ∠ P K L ?

Commented by ajfour last updated on 03/Dec/17

P Q L K i s a n i s o s c e l e s t r a p e z i u m \sqrt{}

I t s b a s e a n g l e s ∠ K P Q i s t h u s

e q u a l t o ∠ P K L (w i t h b a s e P K) .

Commented by Tinkutara last updated on 03/Dec/17

W h y i s o s c e l e s ?

Commented by ajfour last updated on 03/Dec/17

K i s u p p o s e (i n t h e s o l u t i o n p o s t e d

b y y o u) i s r e f l e c t i o n o f P i n A C .

L i s r e f l e c t i o n o f Q i n A C .

Commented by Tinkutara last updated on 03/Dec/17

Thank you Sir!