Question Number 148502 by mathmax by abdo last updated on 28/Jul/21
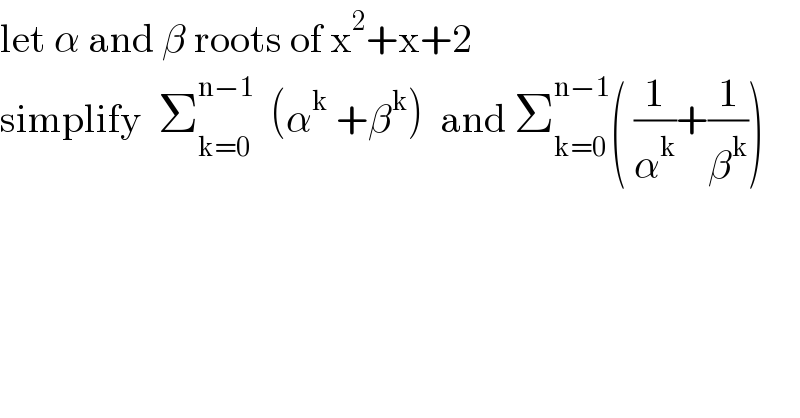
$$\mathrm{let}\:\alpha\:\mathrm{and}\:\beta\:\mathrm{roots}\:\mathrm{of}\:\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{2} \\ $$$$\mathrm{simplify}\:\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \:\:\left(\alpha^{\mathrm{k}} \:+\beta^{\mathrm{k}} \right)\:\:\mathrm{and}\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \left(\:\frac{\mathrm{1}}{\alpha^{\mathrm{k}} }+\frac{\mathrm{1}}{\beta^{\mathrm{k}} }\right) \\ $$
Answered by ArielVyny last updated on 28/Jul/21
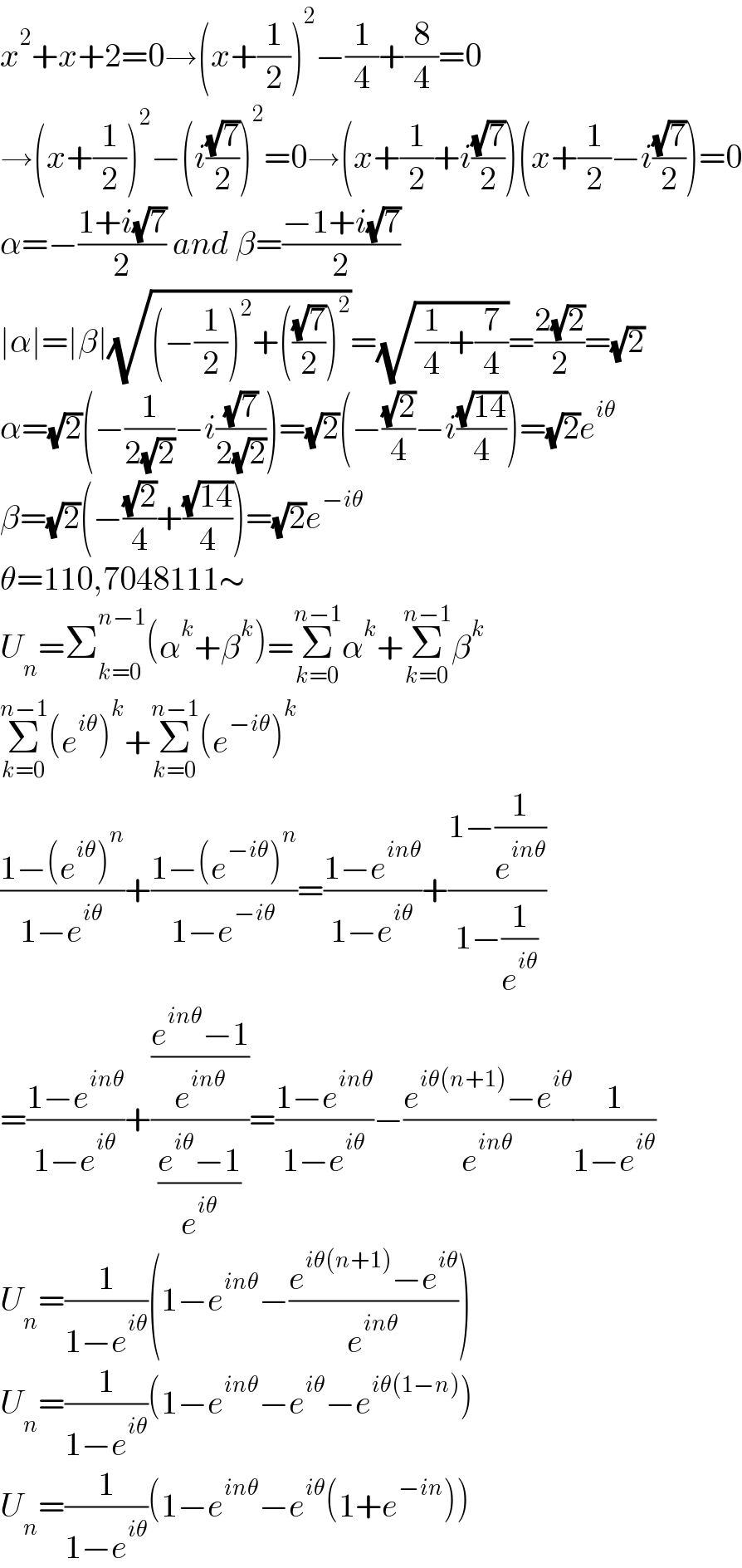
$${x}^{\mathrm{2}} +{x}+\mathrm{2}=\mathrm{0}\rightarrow\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{8}}{\mathrm{4}}=\mathrm{0} \\ $$$$\rightarrow\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\left({i}\frac{\sqrt{\mathrm{7}}}{\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{0}\rightarrow\left({x}+\frac{\mathrm{1}}{\mathrm{2}}+{i}\frac{\sqrt{\mathrm{7}}}{\mathrm{2}}\right)\left({x}+\frac{\mathrm{1}}{\mathrm{2}}−{i}\frac{\sqrt{\mathrm{7}}}{\mathrm{2}}\right)=\mathrm{0} \\ $$$$\alpha=−\frac{\mathrm{1}+{i}\sqrt{\mathrm{7}}}{\mathrm{2}}\:{and}\:\beta=\frac{−\mathrm{1}+{i}\sqrt{\mathrm{7}}}{\mathrm{2}} \\ $$$$\mid\alpha\mid=\mid\beta\mid\sqrt{\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{7}}}{\mathrm{2}}\right)^{\mathrm{2}} }=\sqrt{\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{7}}{\mathrm{4}}}=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{2}}=\sqrt{\mathrm{2}} \\ $$$$\alpha=\sqrt{\mathrm{2}}\left(−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}−{i}\frac{\sqrt{\mathrm{7}}}{\mathrm{2}\sqrt{\mathrm{2}}}\right)=\sqrt{\mathrm{2}}\left(−\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}−{i}\frac{\sqrt{\mathrm{14}}}{\mathrm{4}}\right)=\sqrt{\mathrm{2}}{e}^{{i}\theta} \\ $$$$\beta=\sqrt{\mathrm{2}}\left(−\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}+\frac{\sqrt{\mathrm{14}}}{\mathrm{4}}\right)=\sqrt{\mathrm{2}}{e}^{−{i}\theta} \\ $$$$\theta=\mathrm{110},\mathrm{7048111}\sim \\ $$$${U}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \left(\alpha^{{k}} +\beta^{{k}} \right)=\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\alpha^{{k}} +\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\beta^{{k}} \\ $$$$\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\left({e}^{{i}\theta} \right)^{{k}} +\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\left({e}^{−{i}\theta} \right)^{{k}} \\ $$$$\frac{\mathrm{1}−\left({e}^{{i}\theta} \right)^{{n}} }{\mathrm{1}−{e}^{{i}\theta} }+\frac{\mathrm{1}−\left({e}^{−{i}\theta} \right)^{{n}} }{\mathrm{1}−{e}^{−{i}\theta} }=\frac{\mathrm{1}−{e}^{{in}\theta} }{\mathrm{1}−{e}^{{i}\theta} }+\frac{\mathrm{1}−\frac{\mathrm{1}}{{e}^{{in}\theta} }}{\mathrm{1}−\frac{\mathrm{1}}{{e}^{{i}\theta} }} \\ $$$$=\frac{\mathrm{1}−{e}^{{in}\theta} }{\mathrm{1}−{e}^{{i}\theta} }+\frac{\frac{{e}^{{in}\theta} −\mathrm{1}}{{e}^{{in}\theta} }}{\frac{{e}^{{i}\theta} −\mathrm{1}}{{e}^{{i}\theta} }}=\frac{\mathrm{1}−{e}^{{in}\theta} }{\mathrm{1}−{e}^{{i}\theta} }−\frac{{e}^{{i}\theta\left({n}+\mathrm{1}\right)} −{e}^{{i}\theta} }{{e}^{{in}\theta} }\frac{\mathrm{1}}{\mathrm{1}−{e}^{{i}\theta} } \\ $$$${U}_{{n}} =\frac{\mathrm{1}}{\mathrm{1}−{e}^{{i}\theta} }\left(\mathrm{1}−{e}^{{in}\theta} −\frac{{e}^{{i}\theta\left({n}+\mathrm{1}\right)} −{e}^{{i}\theta} }{{e}^{{in}\theta} }\right) \\ $$$${U}_{{n}} =\frac{\mathrm{1}}{\mathrm{1}−{e}^{{i}\theta} }\left(\mathrm{1}−{e}^{{in}\theta} −{e}^{{i}\theta} −{e}^{{i}\theta\left(\mathrm{1}−{n}\right)} \right) \\ $$$${U}_{{n}} =\frac{\mathrm{1}}{\mathrm{1}−{e}^{{i}\theta} }\left(\mathrm{1}−{e}^{{in}\theta} −{e}^{{i}\theta} \left(\mathrm{1}+{e}^{−{in}} \right)\right) \\ $$
Answered by Olaf_Thorendsen last updated on 28/Jul/21
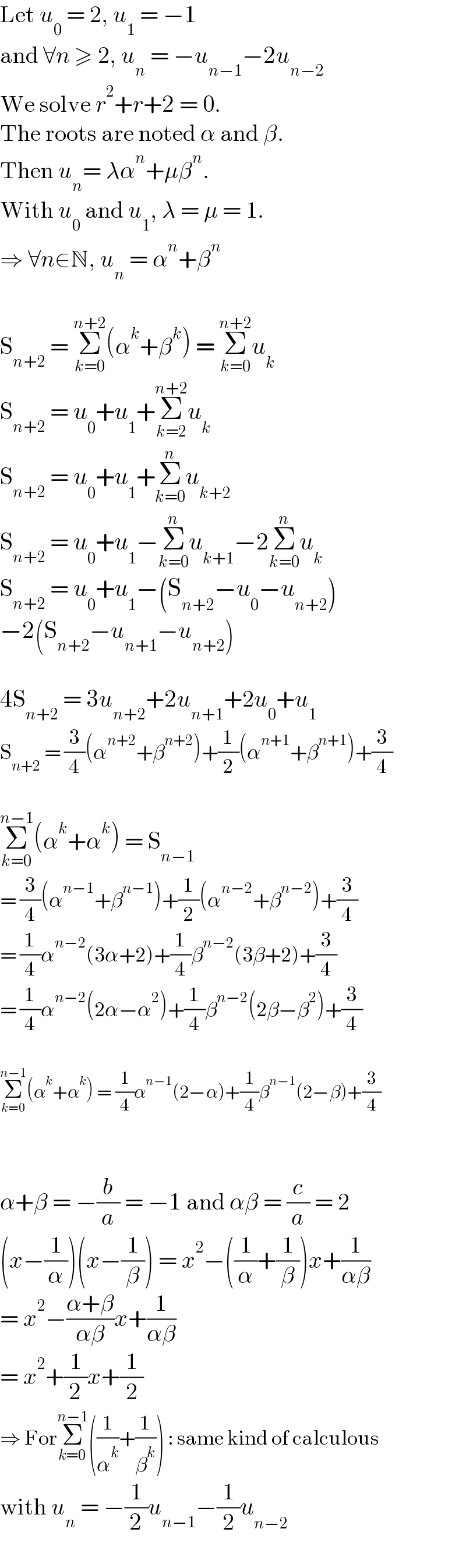
$$\mathrm{Let}\:{u}_{\mathrm{0}} \:=\:\mathrm{2},\:{u}_{\mathrm{1}} \:=\:−\mathrm{1} \\ $$$$\mathrm{and}\:\forall{n}\:\geqslant\:\mathrm{2},\:{u}_{{n}} \:=\:−{u}_{{n}−\mathrm{1}} −\mathrm{2}{u}_{{n}−\mathrm{2}} \\ $$$$\mathrm{We}\:\mathrm{solve}\:{r}^{\mathrm{2}} +{r}+\mathrm{2}\:=\:\mathrm{0}. \\ $$$$\mathrm{The}\:\mathrm{roots}\:\mathrm{are}\:\mathrm{noted}\:\alpha\:\mathrm{and}\:\beta. \\ $$$$\mathrm{Then}\:{u}_{{n}} =\:\lambda\alpha^{{n}} +\mu\beta^{{n}} . \\ $$$$\mathrm{With}\:{u}_{\mathrm{0}} \:\mathrm{and}\:{u}_{\mathrm{1}} ,\:\lambda\:=\:\mu\:=\:\mathrm{1}. \\ $$$$\Rightarrow\:\forall{n}\in\mathbb{N},\:{u}_{{n}} \:=\:\alpha^{{n}} +\beta^{{n}} \\ $$$$ \\ $$$$\mathrm{S}_{{n}+\mathrm{2}} \:=\:\underset{{k}=\mathrm{0}} {\overset{{n}+\mathrm{2}} {\sum}}\left(\alpha^{{k}} +\beta^{{k}} \right)\:=\:\underset{{k}=\mathrm{0}} {\overset{{n}+\mathrm{2}} {\sum}}{u}_{{k}} \\ $$$$\mathrm{S}_{{n}+\mathrm{2}} \:=\:{u}_{\mathrm{0}} +{u}_{\mathrm{1}} +\underset{{k}=\mathrm{2}} {\overset{{n}+\mathrm{2}} {\sum}}{u}_{{k}} \\ $$$$\mathrm{S}_{{n}+\mathrm{2}} \:=\:{u}_{\mathrm{0}} +{u}_{\mathrm{1}} +\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{u}_{{k}+\mathrm{2}} \\ $$$$\mathrm{S}_{{n}+\mathrm{2}} \:=\:{u}_{\mathrm{0}} +{u}_{\mathrm{1}} −\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{u}_{{k}+\mathrm{1}} −\mathrm{2}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{u}_{{k}} \\ $$$$\mathrm{S}_{{n}+\mathrm{2}} \:=\:{u}_{\mathrm{0}} +{u}_{\mathrm{1}} −\left(\mathrm{S}_{{n}+\mathrm{2}} −{u}_{\mathrm{0}} −{u}_{{n}+\mathrm{2}} \right) \\ $$$$−\mathrm{2}\left(\mathrm{S}_{{n}+\mathrm{2}} −{u}_{{n}+\mathrm{1}} −{u}_{{n}+\mathrm{2}} \right) \\ $$$$ \\ $$$$\mathrm{4S}_{{n}+\mathrm{2}} \:=\:\mathrm{3}{u}_{{n}+\mathrm{2}} +\mathrm{2}{u}_{{n}+\mathrm{1}} +\mathrm{2}{u}_{\mathrm{0}} +{u}_{\mathrm{1}} \\ $$$$\mathrm{S}_{{n}+\mathrm{2}} \:=\:\frac{\mathrm{3}}{\mathrm{4}}\left(\alpha^{{n}+\mathrm{2}} +\beta^{{n}+\mathrm{2}} \right)+\frac{\mathrm{1}}{\mathrm{2}}\left(\alpha^{{n}+\mathrm{1}} +\beta^{{n}+\mathrm{1}} \right)+\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$ \\ $$$$\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\left(\alpha^{{k}} +\alpha^{{k}} \right)\:=\:\mathrm{S}_{{n}−\mathrm{1}} \\ $$$$=\:\frac{\mathrm{3}}{\mathrm{4}}\left(\alpha^{{n}−\mathrm{1}} +\beta^{{n}−\mathrm{1}} \right)+\frac{\mathrm{1}}{\mathrm{2}}\left(\alpha^{{n}−\mathrm{2}} +\beta^{{n}−\mathrm{2}} \right)+\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{4}}\alpha^{{n}−\mathrm{2}} \left(\mathrm{3}\alpha+\mathrm{2}\right)+\frac{\mathrm{1}}{\mathrm{4}}\beta^{{n}−\mathrm{2}} \left(\mathrm{3}\beta+\mathrm{2}\right)+\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{4}}\alpha^{{n}−\mathrm{2}} \left(\mathrm{2}\alpha−\alpha^{\mathrm{2}} \right)+\frac{\mathrm{1}}{\mathrm{4}}\beta^{{n}−\mathrm{2}} \left(\mathrm{2}\beta−\beta^{\mathrm{2}} \right)+\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$ \\ $$$$\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\left(\alpha^{{k}} +\alpha^{{k}} \right)\:=\:\frac{\mathrm{1}}{\mathrm{4}}\alpha^{{n}−\mathrm{1}} \left(\mathrm{2}−\alpha\right)+\frac{\mathrm{1}}{\mathrm{4}}\beta^{{n}−\mathrm{1}} \left(\mathrm{2}−\beta\right)+\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$ \\ $$$$ \\ $$$$\alpha+\beta\:=\:−\frac{{b}}{{a}}\:=\:−\mathrm{1}\:\mathrm{and}\:\alpha\beta\:=\:\frac{{c}}{{a}}\:=\:\mathrm{2} \\ $$$$\left({x}−\frac{\mathrm{1}}{\alpha}\right)\left({x}−\frac{\mathrm{1}}{\beta}\right)\:=\:{x}^{\mathrm{2}} −\left(\frac{\mathrm{1}}{\alpha}+\frac{\mathrm{1}}{\beta}\right){x}+\frac{\mathrm{1}}{\alpha\beta} \\ $$$$=\:{x}^{\mathrm{2}} −\frac{\alpha+\beta}{\alpha\beta}{x}+\frac{\mathrm{1}}{\alpha\beta} \\ $$$$=\:{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{x}+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{For}\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\left(\frac{\mathrm{1}}{\alpha^{{k}} }+\frac{\mathrm{1}}{\beta^{{k}} }\right)\::\:\mathrm{same}\:\mathrm{kind}\:\mathrm{of}\:\mathrm{calculous} \\ $$$$\mathrm{with}\:{u}_{{n}} \:=\:−\frac{\mathrm{1}}{\mathrm{2}}{u}_{{n}−\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{2}}{u}_{{n}−\mathrm{2}} \\ $$
Answered by mathmax by abdo last updated on 28/Jul/21

$$\mathrm{x}^{\mathrm{2}\:} +\mathrm{x}+\mathrm{2}=\mathrm{0}\:\rightarrow\Delta=\mathrm{1}−\mathrm{8}=−\mathrm{7}\:\Rightarrow\mathrm{x}_{\mathrm{1}} =\frac{−\mathrm{1}+\mathrm{i}\sqrt{\mathrm{7}}}{\mathrm{2}}\:\mathrm{and}\:\mathrm{x}_{\mathrm{2}} =\frac{−\mathrm{1}−\mathrm{i}\sqrt{\mathrm{7}}}{\mathrm{2}} \\ $$$$\mid\mathrm{x}_{\mathrm{1}} \mid=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{1}+\mathrm{7}}=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{2}}\:\Rightarrow\mathrm{x}_{\mathrm{1}} =\sqrt{\mathrm{2}}\left(\frac{−\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}+\frac{\mathrm{i}\sqrt{\mathrm{7}}}{\mathrm{2}\sqrt{\mathrm{2}}}\right)=\sqrt{\mathrm{2}}\mathrm{e}^{−\mathrm{iarctan}\left(\sqrt{\mathrm{7}}\right)} \\ $$$$\Rightarrow\mathrm{x}_{\mathrm{2}} =\sqrt{\mathrm{2}}\mathrm{e}^{\mathrm{iarctan}\left(\sqrt{\mathrm{7}}\right)} \:\Rightarrow \\ $$$$\mathrm{A}_{\mathrm{n}} =\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \:\alpha^{\mathrm{k}} \:+\beta^{\mathrm{k}} =\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \:\left(\sqrt{\mathrm{2}}\mathrm{e}^{\mathrm{iarctan}\left(\sqrt{\mathrm{7}}\right)} \right)^{\mathrm{k}} \:+\left(\sqrt{\mathrm{2}}\mathrm{e}^{−\mathrm{iarctan}\left(\sqrt{\mathrm{7}}\right)} \right)^{\mathrm{k}} \\ $$$$=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \:\left(\sqrt{\mathrm{2}}\right)^{\mathrm{k}} \left\{\:\mathrm{e}^{\mathrm{ikarctan}\left(\sqrt{\mathrm{7}}\right)} \:\:+\mathrm{e}^{−\mathrm{ikarctan}\left(\sqrt{\mathrm{7}}\right)} \right\} \\ $$$$=\mathrm{2}\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \:\left(\sqrt{\mathrm{2}}\right)^{\mathrm{k}} \:\mathrm{cos}\left(\mathrm{karctan}\left(\sqrt{\mathrm{7}}\right)\right) \\ $$$$\mathrm{let}\:\mathrm{T}_{\mathrm{k}} \left(\mathrm{x}\right)=\mathrm{cos}\left(\mathrm{karctanx}\right)\:\Rightarrow\mathrm{A}_{\mathrm{n}} =\mathrm{2}\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \left(\sqrt{\mathrm{2}}\right)^{\mathrm{k}} \:\mathrm{T}_{\mathrm{k}} \left(\sqrt{\mathrm{7}}\right) \\ $$$$\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \left(\frac{\mathrm{1}}{\alpha^{\mathrm{k}} }+\frac{\mathrm{1}}{\beta^{\mathrm{k}} }\right)=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \left(\frac{\alpha^{\mathrm{k}} \:+\beta^{\mathrm{k}} }{\left(\alpha\beta\right)^{\mathrm{k}} }\right) \\ $$$$=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{k}} }\left(\alpha^{\mathrm{k}} \:+\beta^{\mathrm{k}} \right)\:=\mathrm{2}\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{k}} }\left(\sqrt{\mathrm{2}}\right)^{\mathrm{k}} \:\mathrm{cos}\left(\mathrm{karctan}\left(\sqrt{\mathrm{7}}\right)\right) \\ $$$$=\mathrm{2}\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \:\left(\sqrt{\mathrm{2}}\right)^{−\mathrm{k}} \:\mathrm{T}_{\mathrm{k}} \left(\sqrt{\mathrm{7}}\right) \\ $$$$ \\ $$
