Menu Close

let-and-the-roots-of-the-equation-x-2-2mx-1-0-find-interms-of-the-real-m-A-2-2-B-3-3-c-4-4-D-6-6-

Tinku Tara 0 Comments
Pin




Question Number 37568 by math khazana by abdo last updated on 15/Jun/18
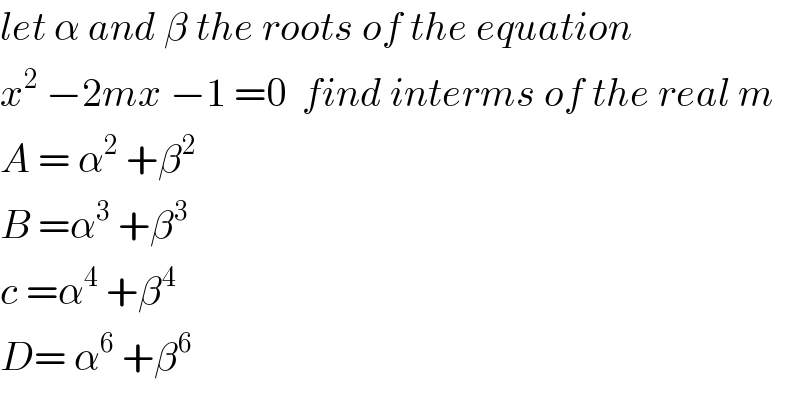
let α and β the roots of the equation x^2 −2mx −1 =0 find interms of the real m A = α^2 +β^2 B =α^3 +β^3 c =α^4 +β^4 D= α^6 +β^6
$${let}\:\alpha\:{and}\:\beta\:{the}\:{roots}\:{of}\:{the}\:{equation} \\ $$$${x}^{\mathrm{2}} \:−\mathrm{2}{mx}\:−\mathrm{1}\:=\mathrm{0}\:\:{find}\:{interms}\:{of}\:{the}\:{real}\:{m} \\ $$$${A}\:=\:\alpha^{\mathrm{2}} \:+\beta^{\mathrm{2}} \\ $$$${B}\:=\alpha^{\mathrm{3}} \:+\beta^{\mathrm{3}} \\ $$$${c}\:=\alpha^{\mathrm{4}} \:+\beta^{\mathrm{4}} \\ $$$${D}=\:\alpha^{\mathrm{6}} \:+\beta^{\mathrm{6}} \\ $$
Answered by Rasheed.Sindhi last updated on 15/Jun/18
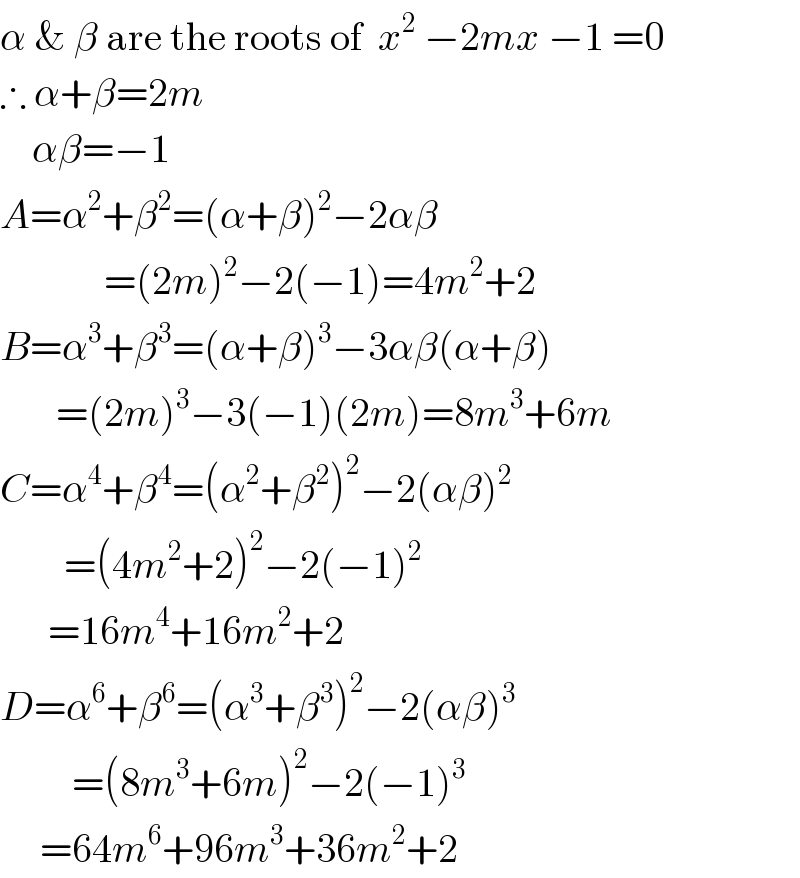
α & β are the roots of x^2 −2mx −1 =0 ∴ α+β=2m αβ=−1 A=α^2 +β^2 =(α+β)^2 −2αβ =(2m)^2 −2(−1)=4m^2 +2 B=α^3 +β^3 =(α+β)^3 −3αβ(α+β) =(2m)^3 −3(−1)(2m)=8m^3 +6m C=α^4 +β^4 =(α^2 +β^2 )^2 −2(αβ)^2 =(4m^2 +2)^2 −2(−1)^2 =16m^4 +16m^2 +2 D=α^6 +β^6 =(α^3 +β^3 )^2 −2(αβ)^3 =(8m^3 +6m)^2 −2(−1)^3 =64m^6 +96m^3 +36m^2 +2
$$\alpha\:\&\:\beta\:\mathrm{are}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:\:{x}^{\mathrm{2}} \:−\mathrm{2}{mx}\:−\mathrm{1}\:=\mathrm{0} \\ $$$$\therefore\:\alpha+\beta=\mathrm{2}{m} \\ $$$$\:\:\:\:\alpha\beta=−\mathrm{1} \\ $$$${A}=\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} =\left(\alpha+\beta\right)^{\mathrm{2}} −\mathrm{2}\alpha\beta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(\mathrm{2}{m}\right)^{\mathrm{2}} −\mathrm{2}\left(−\mathrm{1}\right)=\mathrm{4}{m}^{\mathrm{2}} +\mathrm{2} \\ $$$${B}=\alpha^{\mathrm{3}} +\beta^{\mathrm{3}} =\left(\alpha+\beta\right)^{\mathrm{3}} −\mathrm{3}\alpha\beta\left(\alpha+\beta\right) \\ $$$$\:\:\:\:\:\:\:=\left(\mathrm{2}{m}\right)^{\mathrm{3}} −\mathrm{3}\left(−\mathrm{1}\right)\left(\mathrm{2}{m}\right)=\mathrm{8}{m}^{\mathrm{3}} +\mathrm{6}{m} \\ $$$${C}=\alpha^{\mathrm{4}} +\beta^{\mathrm{4}} =\left(\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{2}\left(\alpha\beta\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:=\left(\mathrm{4}{m}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} −\mathrm{2}\left(−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:=\mathrm{16}{m}^{\mathrm{4}} +\mathrm{16}{m}^{\mathrm{2}} +\mathrm{2} \\ $$$${D}=\alpha^{\mathrm{6}} +\beta^{\mathrm{6}} =\left(\alpha^{\mathrm{3}} +\beta^{\mathrm{3}} \right)^{\mathrm{2}} −\mathrm{2}\left(\alpha\beta\right)^{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:=\left(\mathrm{8}{m}^{\mathrm{3}} +\mathrm{6}{m}\right)^{\mathrm{2}} −\mathrm{2}\left(−\mathrm{1}\right)^{\mathrm{3}} \\ $$$$\:\:\:\:\:=\mathrm{64}{m}^{\mathrm{6}} +\mathrm{96}{m}^{\mathrm{3}} +\mathrm{36}{m}^{\mathrm{2}} +\mathrm{2} \\ $$
Answered by Rio Mike last updated on 16/Jun/18
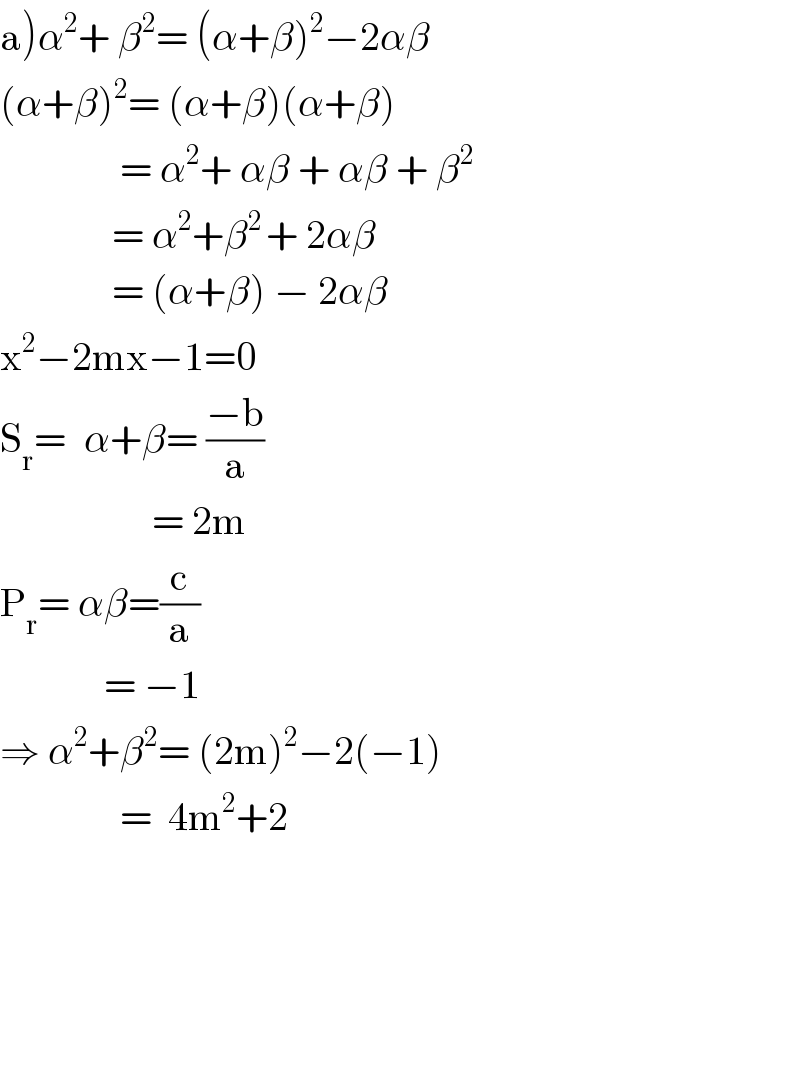
a)α^2 + β^2 = (α+β)^2 −2αβ (α+β)^2 = (α+β)(α+β) = α^2 + αβ + αβ + β^2 = α^2 +β^(2 ) + 2αβ = (α+β) − 2αβ x^2 −2mx−1=0 S_r =^ α+β= ((−b)/a) = 2m P_r = αβ=(c/a) = −1 ⇒ α^2 +β^2 = (2m)^2 −2(−1) = 4m^2 +2
$$\left.\mathrm{a}\right)\alpha^{\mathrm{2}} +\:\beta^{\mathrm{2}} =\:\left(\alpha+\beta\right)^{\mathrm{2}} −\mathrm{2}\alpha\beta \\ $$$$\left(\alpha+\beta\right)^{\mathrm{2}} =\:\left(\alpha+\beta\right)\left(\alpha+\beta\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\alpha^{\mathrm{2}} +\:\alpha\beta\:+\:\alpha\beta\:+\:\beta^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\alpha^{\mathrm{2}} +\beta^{\mathrm{2}\:} +\:\mathrm{2}\alpha\beta\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\left(\alpha+\beta\right)\:−\:\mathrm{2}\alpha\beta \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{2mx}−\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{S}_{\mathrm{r}} =\:^{} \alpha+\beta=\:\frac{−\mathrm{b}}{\mathrm{a}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{2m} \\ $$$$\mathrm{P}_{\mathrm{r}} =\:\alpha\beta=\frac{\mathrm{c}}{\mathrm{a}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\:−\mathrm{1} \\ $$$$\Rightarrow\:\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} =\:\left(\mathrm{2m}\right)^{\mathrm{2}} −\mathrm{2}\left(−\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\:\mathrm{4m}^{\mathrm{2}} +\mathrm{2} \\ $$$$ \\ $$$$\: \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *