Menu Close

let-B-n-0-n-2-arctan-x-2-3y-2-x-2-3y-2-dxdy-calculate-lim-n-B-n-n-

Tinku Tara 0 Comments
Pin




Question Number 104774 by mathmax by abdo last updated on 23/Jul/20
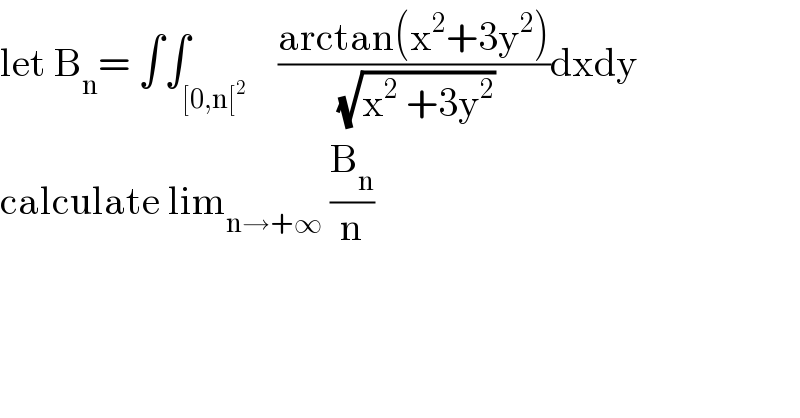
let B_n = ∫∫_([0,n[^2 ) ((arctan(x^2 +3y^2 ))/( (√(x^2 +3y^2 ))))dxdy calculate lim_(n→+∞) (B_n /n)
$$\mathrm{let}\:\mathrm{B}_{\mathrm{n}} =\:\int\int_{\left[\mathrm{0},\mathrm{n}\left[^{\mathrm{2}} \right.\right.} \:\:\:\frac{\mathrm{arctan}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{3y}^{\mathrm{2}} \right)}{\:\sqrt{\mathrm{x}^{\mathrm{2}} \:+\mathrm{3y}^{\mathrm{2}} }}\mathrm{dxdy} \\ $$$$\mathrm{calculate}\:\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\frac{\mathrm{B}_{\mathrm{n}} }{\mathrm{n}} \\ $$
Answered by mathmax by abdo last updated on 26/Jul/20
we do the changement { ((x =rcosθ)),((y =(r/( (√3)))sinθ)) :} we hsve 0≤x<n and 0≤y <n ⇒0 ≤x^2 +3y^2 <4n^2 ⇒ 0≤r^2 <4n^2 ⇒0≤r<2n ⇒B_n =∫_0 ^(2n) ∫_0 ^(π/2) ((arctan(r^2 ))/r) r dr dθ =(π/2) ∫_0 ^(2n) arctan(r^2 )dr by psrts ∫ arctan(r^2 )dr =r arctan(r^2 )−∫ r×((2r)/(1+r^4 ))dr =r arctan(r^2 )−2 ∫ (r^2 /(1+r^4 ))dr and ∫ (r^2 /(1+r^4 )) dr =∫ (1/((1/r^2 ) +r^2 ))dr =(1/2)∫ ((1−(1/r^2 )+1+(1/r^2 ))/(r^2 +(1/r^2 )))dr =(1/2) ∫ (((1−(1/r^2 ))dr)/((r+(1/r))^2 −2))(→u =r+(1/r))+(1/2)∫ (((1+(1/r^2 ))dr)/((r−(1/r))^2 +2))(v=r−(1/r)) =(1/2)∫ (du/(u^2 −2)) +(1/2)∫ (dv/(v^2 +2))(→v =(√2)α) =(1/(4(√2)))∫((1/(u−(√2)))−(1/(u+(√2))))du +(1/2)∫ (((√2)dα)/(2(1+α^2 ))) =(1/(4(√2)))ln∣((u−(√2))/(u+(√2)))∣ +(1/(2(√2))) arctan((v/( (√2)))) +c =(1/(4(√2)))ln∣((r+(1/r)−(√2))/(r+(1/r)+(√2)))∣+(1/(2(√2))) arctan((1/( (√2)))(r−(1/r))) +c
$$\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\begin{cases}{\mathrm{x}\:=\mathrm{rcos}\theta}\\{\mathrm{y}\:=\frac{\mathrm{r}}{\:\sqrt{\mathrm{3}}}\mathrm{sin}\theta}\end{cases} \\ $$$$\mathrm{we}\:\mathrm{hsve}\:\mathrm{0}\leqslant\mathrm{x}<\mathrm{n}\:\mathrm{and}\:\mathrm{0}\leqslant\mathrm{y}\:<\mathrm{n}\:\Rightarrow\mathrm{0}\:\leqslant\mathrm{x}^{\mathrm{2}} \:+\mathrm{3y}^{\mathrm{2}} \:<\mathrm{4n}^{\mathrm{2}} \:\Rightarrow \\ $$$$\mathrm{0}\leqslant\mathrm{r}^{\mathrm{2}} <\mathrm{4n}^{\mathrm{2}} \:\Rightarrow\mathrm{0}\leqslant\mathrm{r}<\mathrm{2n}\:\Rightarrow\mathrm{B}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{2n}} \int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{arctan}\left(\mathrm{r}^{\mathrm{2}} \right)}{\mathrm{r}}\:\mathrm{r}\:\mathrm{dr}\:\mathrm{d}\theta \\ $$$$=\frac{\pi}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\mathrm{2n}} \:\mathrm{arctan}\left(\mathrm{r}^{\mathrm{2}} \right)\mathrm{dr}\:\:\mathrm{by}\:\mathrm{psrts}\: \\ $$$$\int\:\:\mathrm{arctan}\left(\mathrm{r}^{\mathrm{2}} \right)\mathrm{dr}\:=\mathrm{r}\:\mathrm{arctan}\left(\mathrm{r}^{\mathrm{2}} \right)−\int\:\mathrm{r}×\frac{\mathrm{2r}}{\mathrm{1}+\mathrm{r}^{\mathrm{4}} }\mathrm{dr} \\ $$$$=\mathrm{r}\:\mathrm{arctan}\left(\mathrm{r}^{\mathrm{2}} \right)−\mathrm{2}\:\int\:\frac{\mathrm{r}^{\mathrm{2}} }{\mathrm{1}+\mathrm{r}^{\mathrm{4}} }\mathrm{dr}\:\mathrm{and} \\ $$$$\int\:\frac{\mathrm{r}^{\mathrm{2}} }{\mathrm{1}+\mathrm{r}^{\mathrm{4}} }\:\mathrm{dr}\:=\int\:\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{r}^{\mathrm{2}} }\:+\mathrm{r}^{\mathrm{2}} }\mathrm{dr}\:=\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{r}^{\mathrm{2}} }+\mathrm{1}+\frac{\mathrm{1}}{\mathrm{r}^{\mathrm{2}} }}{\mathrm{r}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{r}^{\mathrm{2}} }}\mathrm{dr} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\frac{\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{r}^{\mathrm{2}} }\right)\mathrm{dr}}{\left(\mathrm{r}+\frac{\mathrm{1}}{\mathrm{r}}\right)^{\mathrm{2}} −\mathrm{2}}\left(\rightarrow\mathrm{u}\:=\mathrm{r}+\frac{\mathrm{1}}{\mathrm{r}}\right)+\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\frac{\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{r}^{\mathrm{2}} }\right)\mathrm{dr}}{\left(\mathrm{r}−\frac{\mathrm{1}}{\mathrm{r}}\right)^{\mathrm{2}} \:+\mathrm{2}}\left(\mathrm{v}=\mathrm{r}−\frac{\mathrm{1}}{\mathrm{r}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} −\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{dv}}{\mathrm{v}^{\mathrm{2}} \:+\mathrm{2}}\left(\rightarrow\mathrm{v}\:=\sqrt{\mathrm{2}}\alpha\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\int\left(\frac{\mathrm{1}}{\mathrm{u}−\sqrt{\mathrm{2}}}−\frac{\mathrm{1}}{\mathrm{u}+\sqrt{\mathrm{2}}}\right)\mathrm{du}\:+\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\sqrt{\mathrm{2}}\mathrm{d}\alpha}{\mathrm{2}\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\mathrm{ln}\mid\frac{\mathrm{u}−\sqrt{\mathrm{2}}}{\mathrm{u}+\sqrt{\mathrm{2}}}\mid\:+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\mathrm{arctan}\left(\frac{\mathrm{v}}{\:\sqrt{\mathrm{2}}}\right)\:+\mathrm{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\mathrm{ln}\mid\frac{\mathrm{r}+\frac{\mathrm{1}}{\mathrm{r}}−\sqrt{\mathrm{2}}}{\mathrm{r}+\frac{\mathrm{1}}{\mathrm{r}}+\sqrt{\mathrm{2}}}\mid+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\mathrm{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\mathrm{r}−\frac{\mathrm{1}}{\mathrm{r}}\right)\right)\:+\mathrm{c} \\ $$
Commented by mathmax by abdo last updated on 26/Jul/20
=(1/(2(√2))){ ln((√((r+(1/r)−(√2))/(r+(1/r)+(√2))))) +arctan((1/( (√2)))(r−(1/r))) +c ⇒ ∫_0 ^(2n) arctan(r^2 )dr =[r arctan(r^2 )]_0 ^(2n) −(1/( (√2)))[{ln((√((r^2 +1−(√2)r)/(r^2 +1+(√2)r)))) +arctan((1/( (√2)))(r−(1/r)))]_0 ^(2n) =2n arctan(4n^2 )−(1/( (√2))){ln((√((4n^2 +1−2(√2)n)/(4n^2 +1+2(√2)n))))+arctan((1/( (√2)))(2n−(1/(2n)))=u_n +(π/2)} ⇒B_n =(π/2)u_n ⇒(B_n /n) =(π/2)(u_n /n) =π arctan(4n^2 ) −(1/(n(√2))){ln(√((4n^2 +1−2(√2)n)/(4n^2 +1+2(√2)n)))+arctan((1/( (√2)))(2n−(1/n))} ⇒lim_(n→+∞) (B_n /n) =π×(π/2) =(π^2 /2)
$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\left\{\:\mathrm{ln}\left(\sqrt{\frac{\mathrm{r}+\frac{\mathrm{1}}{\mathrm{r}}−\sqrt{\mathrm{2}}}{\mathrm{r}+\frac{\mathrm{1}}{\mathrm{r}}+\sqrt{\mathrm{2}}}}\right)\:+\mathrm{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\mathrm{r}−\frac{\mathrm{1}}{\mathrm{r}}\right)\right)\:+\mathrm{c}\:\Rightarrow\right. \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2n}} \:\mathrm{arctan}\left(\mathrm{r}^{\mathrm{2}} \right)\mathrm{dr}\:=\left[\mathrm{r}\:\mathrm{arctan}\left(\mathrm{r}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\mathrm{2n}} \:−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left[\left\{\mathrm{ln}\left(\sqrt{\frac{\mathrm{r}^{\mathrm{2}} +\mathrm{1}−\sqrt{\mathrm{2}}\mathrm{r}}{\mathrm{r}^{\mathrm{2}} \:+\mathrm{1}+\sqrt{\mathrm{2}}\mathrm{r}}}\right)\right.\right. \\ $$$$\left.+\mathrm{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\mathrm{r}−\frac{\mathrm{1}}{\mathrm{r}}\right)\right)\right]_{\mathrm{0}} ^{\mathrm{2n}} \\ $$$$=\mathrm{2n}\:\mathrm{arctan}\left(\mathrm{4n}^{\mathrm{2}} \right)−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left\{\mathrm{ln}\left(\sqrt{\frac{\mathrm{4n}^{\mathrm{2}} +\mathrm{1}−\mathrm{2}\sqrt{\mathrm{2}}\mathrm{n}}{\mathrm{4n}^{\mathrm{2}} \:+\mathrm{1}+\mathrm{2}\sqrt{\mathrm{2}}\mathrm{n}}}\right)+\mathrm{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\mathrm{2n}−\frac{\mathrm{1}}{\mathrm{2n}}\right)=\mathrm{u}_{\mathrm{n}} \right.\right. \\ $$$$\left.+\frac{\pi}{\mathrm{2}}\right\}\:\Rightarrow\mathrm{B}_{\mathrm{n}} =\frac{\pi}{\mathrm{2}}\mathrm{u}_{\mathrm{n}} \:\Rightarrow\frac{\mathrm{B}_{\mathrm{n}} }{\mathrm{n}}\:=\frac{\pi}{\mathrm{2}}\frac{\mathrm{u}_{\mathrm{n}} }{\mathrm{n}} \\ $$$$=\pi\:\mathrm{arctan}\left(\mathrm{4n}^{\mathrm{2}} \right)\:−\frac{\mathrm{1}}{\mathrm{n}\sqrt{\mathrm{2}}}\left\{\mathrm{ln}\sqrt{\frac{\mathrm{4n}^{\mathrm{2}} \:+\mathrm{1}−\mathrm{2}\sqrt{\mathrm{2}}\mathrm{n}}{\mathrm{4n}^{\mathrm{2}} \:+\mathrm{1}+\mathrm{2}\sqrt{\mathrm{2}}\mathrm{n}}}+\mathrm{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\mathrm{2n}−\frac{\mathrm{1}}{\mathrm{n}}\right)\right\}\right. \\ $$$$\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\frac{\mathrm{B}_{\mathrm{n}} }{\mathrm{n}}\:=\pi×\frac{\pi}{\mathrm{2}}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{2}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *