Question Number 40892 by abdo.msup.com last updated on 28/Jul/18
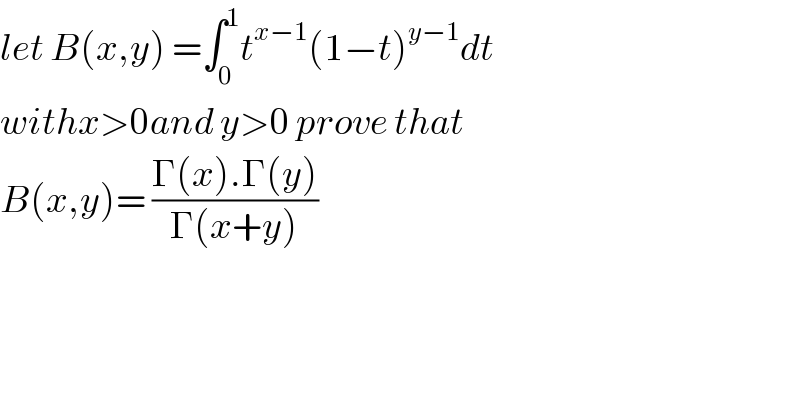
$${let}\:{B}\left({x},{y}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{{x}−\mathrm{1}} \left(\mathrm{1}−{t}\right)^{{y}−\mathrm{1}} {dt} \\ $$$${withx}>\mathrm{0}{and}\:{y}>\mathrm{0}\:{prove}\:{that} \\ $$$${B}\left({x},{y}\right)=\:\frac{\Gamma\left({x}\right).\Gamma\left({y}\right)}{\Gamma\left({x}+{y}\right)} \\ $$
