let-be-a-root-of-the-equation-x-4-x-1-4-1-0-find-300-301-

Question Number 158124 by HongKing last updated on 31/Oct/21

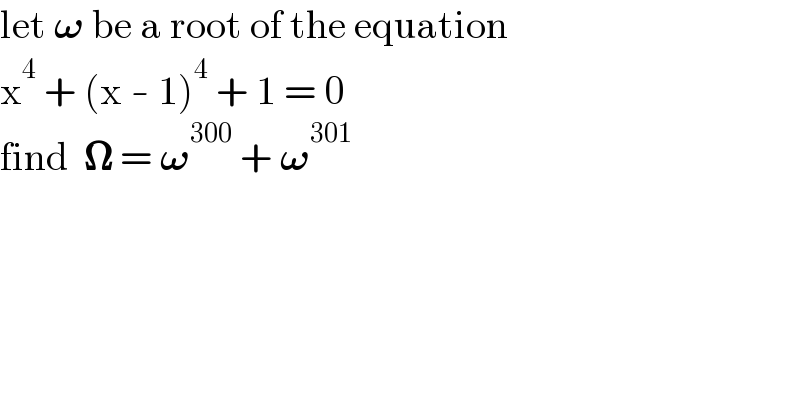
let 𝛚 be a root of the equation x^4 + (x - 1)^4 + 1 = 0 find 𝛀 = 𝛚^(300) + 𝛚^(301)

$$\mathrm{let}\:\boldsymbol{\omega}\:\mathrm{be}\:\mathrm{a}\:\mathrm{root}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\mathrm{x}^{\mathrm{4}} \:+\:\left(\mathrm{x}\:-\:\mathrm{1}\right)^{\mathrm{4}} \:+\:\mathrm{1}\:=\:\mathrm{0} \\ $$$$\mathrm{find}\:\:\boldsymbol{\Omega}\:=\:\boldsymbol{\omega}^{\mathrm{300}} \:+\:\boldsymbol{\omega}^{\mathrm{301}} \\ $$

Answered by Rasheed.Sindhi last updated on 31/Oct/21

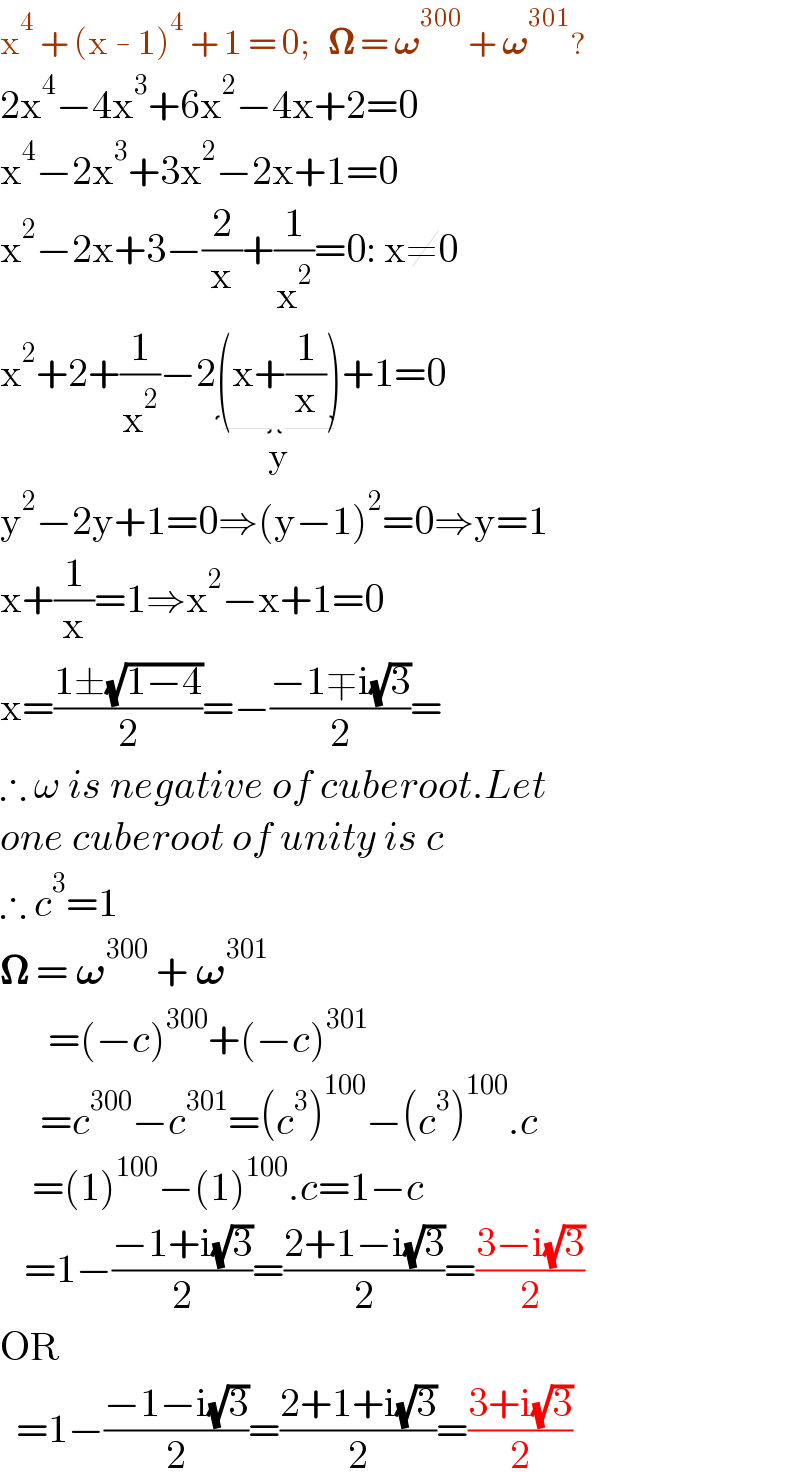
x^4 + (x - 1)^4 + 1 = 0; 𝛀 = 𝛚^(300) + 𝛚^(301) ? 2x^4 −4x^3 +6x^2 −4x+2=0 x^4 −2x^3 +3x^2 −2x+1=0 x^2 −2x+3−(2/x)+(1/x^2 )=0: x≠0 x^2 +2+(1/x^2 )−2(x+(1/x))_(y) +1=0 y^2 −2y+1=0⇒(y−1)^2 =0⇒y=1 x+(1/x)=1⇒x^2 −x+1=0 x=((1±(√(1−4)))/2)=−((−1∓i(√3))/2)= ∴ ω is negative of cuberoot.Let one cuberoot of unity is c ∴ c^3 =1 𝛀 = 𝛚^(300) + 𝛚^(301) =(−c)^(300) +(−c)^(301) =c^(300) −c^(301) =(c^3 )^(100) −(c^3 )^(100) .c =(1)^(100) −(1)^(100) .c=1−c =1−((−1+i(√3))/2)=((2+1−i(√3))/2)=((3−i(√3))/2) OR =1−((−1−i(√3))/2)=((2+1+i(√3))/2)=((3+i(√3))/2)

$$\mathrm{x}^{\mathrm{4}} \:+\:\left(\mathrm{x}\:-\:\mathrm{1}\right)^{\mathrm{4}} \:+\:\mathrm{1}\:=\:\mathrm{0};\:\:\:\boldsymbol{\Omega}\:=\:\boldsymbol{\omega}^{\mathrm{300}} \:+\:\boldsymbol{\omega}^{\mathrm{301}} ? \\ $$$$\mathrm{2x}^{\mathrm{4}} −\mathrm{4x}^{\mathrm{3}} +\mathrm{6x}^{\mathrm{2}} −\mathrm{4x}+\mathrm{2}=\mathrm{0} \\ $$$$\mathrm{x}^{\mathrm{4}} −\mathrm{2x}^{\mathrm{3}} +\mathrm{3x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{3}−\frac{\mathrm{2}}{\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }=\mathrm{0}:\:\mathrm{x}\neq\mathrm{0} \\ $$$$\mathrm{x}^{\mathrm{2}} +\mathrm{2}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }−\mathrm{2}\underset{\mathrm{y}} {\underbrace{\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)}}+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{y}^{\mathrm{2}} −\mathrm{2y}+\mathrm{1}=\mathrm{0}\Rightarrow\left(\mathrm{y}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{0}\Rightarrow\mathrm{y}=\mathrm{1} \\ $$$$\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}=\mathrm{1}\Rightarrow\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{x}=\frac{\mathrm{1}\pm\sqrt{\mathrm{1}−\mathrm{4}}}{\mathrm{2}}=−\frac{−\mathrm{1}\mp\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}= \\ $$$$\therefore\:\omega\:{is}\:{negative}\:{of}\:{cuberoot}.{Let} \\ $$$${one}\:{cuberoot}\:{of}\:{unity}\:{is}\:{c} \\ $$$$\therefore\:{c}^{\mathrm{3}} =\mathrm{1} \\ $$$$\boldsymbol{\Omega}\:=\:\boldsymbol{\omega}^{\mathrm{300}} \:+\:\boldsymbol{\omega}^{\mathrm{301}} \:\: \\ $$$$\:\:\:\:\:\:=\left(−{c}\right)^{\mathrm{300}} +\left(−{c}\right)^{\mathrm{301}} \\ $$$$\:\:\:\:\:={c}^{\mathrm{300}} −{c}^{\mathrm{301}} =\left({c}^{\mathrm{3}} \right)^{\mathrm{100}} −\left({c}^{\mathrm{3}} \right)^{\mathrm{100}} .{c} \\ $$$$\:\:\:\:=\left(\mathrm{1}\right)^{\mathrm{100}} −\left(\mathrm{1}\right)^{\mathrm{100}} .{c}=\mathrm{1}−{c} \\ $$$$\:\:\:=\mathrm{1}−\frac{−\mathrm{1}+\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}=\frac{\mathrm{2}+\mathrm{1}−\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}=\frac{\mathrm{3}−\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\mathrm{OR}\: \\ $$$$\:\:=\mathrm{1}−\frac{−\mathrm{1}−\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}=\frac{\mathrm{2}+\mathrm{1}+\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}=\frac{\mathrm{3}+\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$

Commented by mr W last updated on 04/Nov/21

ω^3 =−1 is correct. Ω=((3±i(√3))/2) is correct. but Ω≠0

$$\omega^{\mathrm{3}} =−\mathrm{1}\:{is}\:{correct}. \\ $$$$\Omega=\frac{\mathrm{3}\pm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\:{is}\:{correct}. \\ $$$${but}\:\Omega\neq\mathrm{0} \\ $$

Commented by HongKing last updated on 31/Oct/21

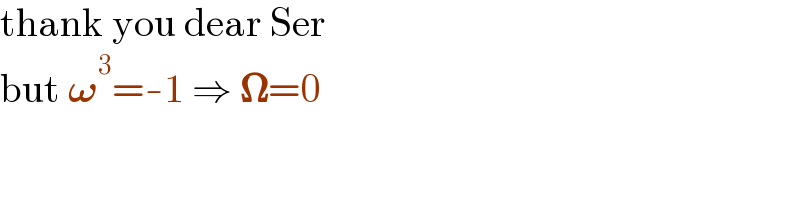
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{dear}\:\mathrm{Ser} \\ $$$$\mathrm{but}\:\boldsymbol{\omega}^{\mathrm{3}} =-\mathrm{1}\:\Rightarrow\:\boldsymbol{\Omega}=\mathrm{0} \\ $$

Commented by Rasheed.Sindhi last updated on 31/Oct/21

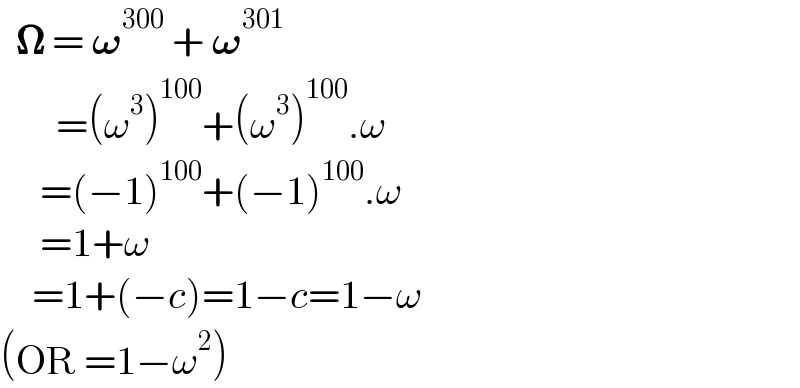
𝛀 = 𝛚^(300) + 𝛚^(301) =(ω^3 )^(100) +(ω^3 )^(100) .ω =(−1)^(100) +(−1)^(100) .ω =1+ω =1+(−c)=1−c=1−ω (OR =1−ω^2 )

$$\:\:\boldsymbol{\Omega}\:=\:\boldsymbol{\omega}^{\mathrm{300}} \:+\:\boldsymbol{\omega}^{\mathrm{301}} \\ $$$$\:\:\:\:\:\:\:=\left(\omega^{\mathrm{3}} \right)^{\mathrm{100}} +\left(\omega^{\mathrm{3}} \right)^{\mathrm{100}} .\omega \\ $$$$\:\:\:\:\:=\left(−\mathrm{1}\right)^{\mathrm{100}} +\left(−\mathrm{1}\right)^{\mathrm{100}} .\omega \\ $$$$\:\:\:\:\:=\mathrm{1}+\omega \\ $$$$\:\:\:\:=\mathrm{1}+\left(−{c}\right)=\mathrm{1}−{c}=\mathrm{1}−\omega \\ $$$$\left(\mathrm{OR}\:=\mathrm{1}−\omega^{\mathrm{2}} \right) \\ $$

Commented by Rasheed.Sindhi last updated on 01/Nov/21