Let-consider-A-3-5-B-6-4-and-C-3-2-d-x-5y-7-0-Consider-a-dot-D-such-as-ABCD-is-a-trapezium-and-AD-and-BC-are-parallel-lines-Q1-Give-the-equation-of-the-line-which-contains-the-point-

FacebookTweetPin

Question Number 45649 by hassentimol last updated on 15/Oct/18

$$\mathrm{Let}\mathrm{consider}\mathrm{A}(3,5),\mathrm{B}(6,4)\mathrm{and}\mathrm{C}(3,-2),$$$$\mathrm{d}:x-5y+7=0$$$$$$$$\mathrm{Consider}\mathrm{a}\mathrm{dot}\mathrm{D}\mathrm{such}\mathrm{as}\mathrm{ABCD}\mathrm{is}\mathrm{a}\mathrm{trapezium}$$$$\mathrm{and}\left(\mathrm{AD}\right)\mathrm{and}\left(\mathrm{BC}\right)\mathrm{are}\mathrm{parallel}\mathrm{lines}.$$$$$$$$\mathrm{Q}1)\mathrm{Give}\mathrm{the}\mathrm{equation}\mathrm{of}\mathrm{the}\mathrm{line}\mathrm{which}$$$$\mathrm{contains}\mathrm{the}\mathrm{point}\mathrm{D}.$$$$$$$$\mathrm{Q}2)\mathrm{Considering}\mathrm{that}\mathrm{the}\mathrm{trapezium}$$$$\mathrm{should}\mathrm{be}\mathrm{convex},\mathrm{are}\mathrm{all}\mathrm{the}\mathrm{points}\mathrm{D}\mathrm{of}$$$$\mathrm{the}\mathrm{lines}\mathrm{correct}\mathrm{for}\mathrm{the}\mathrm{Trapezium}?$$$$\mathrm{Which}\mathrm{ones}\mathrm{are}?$$$$\mathrm{Give}\mathrm{a}\mathrm{proof}.$$$$$$$$$$$$\mathrm{I}\mathrm{have}\mathrm{some}\mathrm{difficulties}\mathrm{to}\mathrm{anzwer}\mathrm{the}$$$$\mathrm{question}\mathrm{n}°2,\mathrm{could}\mathrm{someone}\mathrm{please},$$$$\mathrm{help}\mathrm{me}.$$$$$$$$\mathrm{Thank}\mathrm{you}.$$$$$$$$\mathrm{H}.\mathrm{T}.$$

Commented by hassentimol last updated on 15/Oct/18

$$$$$$$$$$$$$$$$$$$$$$\mathrm{Could}\mathrm{you}\mathrm{help}\mathrm{me}\mathrm{for}\mathrm{Question}\mathrm{n}°2?$$$$\mathrm{How}\mathrm{may}\mathrm{I}\mathrm{proove}?$$

Answered by tanmay.chaudhury50@gmail.com last updated on 15/Oct/18

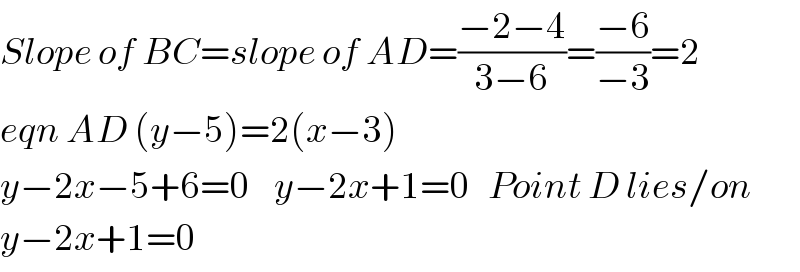
$$SlopeofBC=slopeofAD=\frac{-2-4}{3-6}=\frac{-6}{-3}=2$$$$eqnAD(y-5)=2(x-3)$$$$y-2x-5+6=0y-2x+1=0PointDlies/on$$$$y-2x+1=0$$

Commented by hassentimol last updated on 15/Oct/18

$$$$$$$$$$Thankyouverymuchsir!$$$$$$$$\mathrm{Could}\mathrm{you}\mathrm{help}\mathrm{me}\mathrm{for}\mathrm{question}\mathrm{n}°2;\mathrm{I}\mathrm{have}$$$$\mathrm{understood}\mathrm{that}\mathrm{the}\mathrm{dot}\mathrm{D}\mathrm{should}\mathrm{be}\mathrm{like}:$$$$x_D<3,\mathrm{because}\mathrm{the}\mathrm{lines}\mathrm{of}\mathrm{the}\mathrm{trapezium}$$$$\mathrm{must}\mathrm{not}\mathrm{be}\mathrm{crossed}\left(\mathrm{as}\mathrm{they}\mathrm{are}\mathrm{convex}\right),\mathrm{however},\mathrm{how}\mathrm{could}\mathrm{I}$$$$\mathrm{give}\mathrm{a}\mathrm{proof}\mathrm{to}\mathrm{the}\mathrm{answer}?$$$$$$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com

FacebookTweetPin