Question Number 119401 by cantor last updated on 24/Oct/20

$$\boldsymbol{{let}}\:\boldsymbol{{d}}\:\boldsymbol{{be}}\:\boldsymbol{{an}}\:\boldsymbol{{application}} \\ $$$$\boldsymbol{{d}}:\mathbb{R}^{\mathrm{2}} \rightarrow\mathbb{R}_{+} \\ $$$$\boldsymbol{{d}}\left(\boldsymbol{{x}},\boldsymbol{{y}}\right)=\boldsymbol{{ln}}\left(\mathrm{1}+\frac{\mid\boldsymbol{{x}}−\boldsymbol{{y}}\mid}{\mathrm{1}+\mid\boldsymbol{{x}}−\boldsymbol{{y}}\mid}\right) \\ $$$$\boldsymbol{{shown}}\:\boldsymbol{{that}}\:\boldsymbol{{d}}\:\boldsymbol{{is}}\:\boldsymbol{{a}}\:\boldsymbol{{distance}} \\ $$$$\boldsymbol{{on}}\:\mathbb{R}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{please}}\:\boldsymbol{{help}}\: \\ $$$$\:\bigstar\boldsymbol{{especially}}\:\boldsymbol{{on}}\:\boldsymbol{{triangular}} \\ $$$$\boldsymbol{{inequality}} \\ $$
Answered by mindispower last updated on 24/Oct/20

$${d}\left({x},{y}\right)\geqslant\mathrm{0},\forall\left({x},{y}\right)\in\mathbb{R}^{\mathrm{2}} \\ $$$${d}\left({x},{y}\right)+{d}\left({y},{z}\right) \\ $$$$\frac{\mid{x}−{y}\mid}{\mathrm{1}+\mid{x}−{y}\mid}={f}\left(\mid{x}−{y}\mid\right) \\ $$$${f}\left({x}\right)=\frac{{x}}{\mathrm{1}+{x}} \\ $$$${f}\left({a}\right)+{f}\left({b}\right)\geqslant{f}\left({a}+{b}\right),\forall\left({a}.{b}\right)\in\mathbb{R}_{+} ^{\mathrm{2}} ..? \\ $$$$\Leftrightarrow\frac{{a}}{\mathrm{1}+{a}}+\frac{{b}}{\mathrm{1}+{b}}\geqslant\frac{{a}+{b}}{{a}+{b}+\mathrm{1}}..{A} \\ $$$$\Leftrightarrow\frac{\mathrm{2}{ab}+{a}+{b}}{\left(\mathrm{1}+{a}\right)\left(\mathrm{1}+{b}\right)}\geqslant\frac{{a}+{b}}{\left({a}+{b}+\mathrm{1}\right)} \\ $$$$\Leftrightarrow\frac{\mathrm{2}{ab}+{a}+{b}}{{a}+{b}+\mathrm{1}+{ab}}\geqslant\frac{{a}+{b}}{{a}+{b}+\mathrm{1}} \\ $$$$\frac{{ab}}{{a}+{b}+\mathrm{1}+{ab}}+\frac{{ab}+{a}+{b}}{{a}+{b}+{ab}+\mathrm{1}}\geqslant\frac{{a}+{b}}{{a}+{b}+\mathrm{1}} \\ $$$${f}\left({t}\right)=\frac{{t}}{{t}+\mathrm{1}},{f}'\left({t}\right)=\frac{\mathrm{1}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }\geqslant\mathrm{0}\:{f}\:{increse} \\ $$$${ab}+{a}+{b}\geqslant{a}+{b},\:\:{ab}\geqslant\mathrm{0}, \\ $$$$\Rightarrow{f}\left({ab}+{a}+{b}\right)\geqslant{f}\left({a}+{b}\right) \\ $$$$\Leftrightarrow\frac{{ab}+{a}+{b}}{{ab}+{a}+{b}+\mathrm{1}}+\frac{{ab}}{{ab}+{a}+{b}+\mathrm{1}}\geqslant\frac{{ab}+{a}+{b}}{{ab}+{a}+{b}+\mathrm{1}}\geqslant\frac{{a}+{b}}{{a}+{b}+\mathrm{1}} \\ $$$$\Rightarrow{A}\:{is}\:{true}\: \\ $$$$\frac{\mid{x}−{y}\mid}{\mathrm{1}+\mid{x}−{y}\mid}+\frac{\mid{y}−{z}\mid}{\mathrm{1}+\mid{y}−{z}\mid}\geqslant\frac{\mid{x}−{y}\mid+\mid{y}−{z}\mid}{\mathrm{1}+\mid{x}−{y}\mid+\mid{y}−{z}\mid}\geqslant\frac{\mid{x}−{z}\mid}{\mathrm{1}+\mid{x}−{z}\mid} \\ $$$${since}\:\mid{x}−{y}\mid+\mid{y}−{z}\mid\geqslant\mid{x}−{z}\mid \\ $$$${and}\:{f}\:{is}\:{increase}\:{function} \\ $$$${ln}\left(\mathrm{1}+{a}\right)+{ln}\left(\mathrm{1}+{b}\right)\geqslant{ln}\left(\mathrm{1}+{a}+{b}\right)…… \\ $$$${this}\:{show}\:{inequality} \\ $$$$ \\ $$$$ \\ $$
Answered by 1549442205PVT last updated on 24/Oct/20
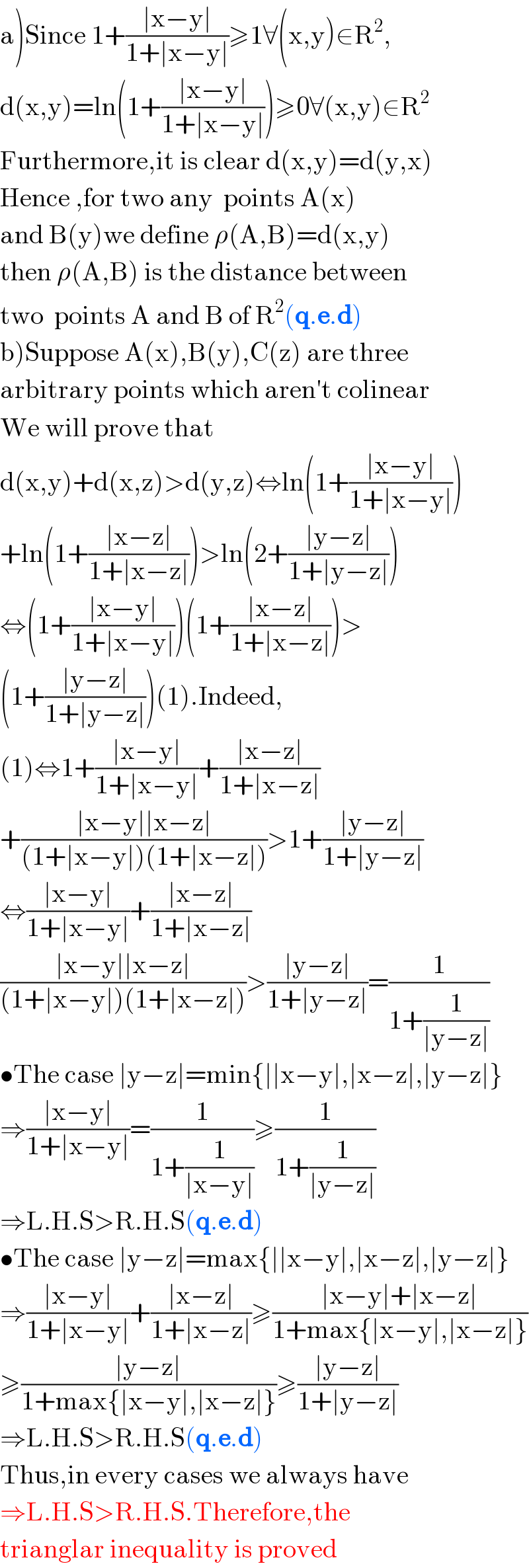
$$\left.\mathrm{a}\right)\mathrm{Since}\:\mathrm{1}+\frac{\mid\mathrm{x}−\mathrm{y}\mid}{\mathrm{1}+\mid\mathrm{x}−\mathrm{y}\mid}\geqslant\mathrm{1}\forall\left(\mathrm{x},\mathrm{y}\right)\in\mathrm{R}^{\mathrm{2}} , \\ $$$$\mathrm{d}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{ln}\left(\mathrm{1}+\frac{\mid\mathrm{x}−\mathrm{y}\mid}{\mathrm{1}+\mid\mathrm{x}−\mathrm{y}\mid}\right)\geqslant\mathrm{0}\forall\left(\mathrm{x},\mathrm{y}\right)\in\mathrm{R}^{\mathrm{2}} \\ $$$$\mathrm{Furthermore},\mathrm{it}\:\mathrm{is}\:\mathrm{clear}\:\mathrm{d}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{d}\left(\mathrm{y},\mathrm{x}\right) \\ $$$$\mathrm{Hence}\:,\mathrm{for}\:\mathrm{two}\:\mathrm{any}\:\:\mathrm{points}\:\mathrm{A}\left(\mathrm{x}\right) \\ $$$$\mathrm{and}\:\mathrm{B}\left(\mathrm{y}\right)\mathrm{we}\:\mathrm{define}\:\rho\left(\mathrm{A},\mathrm{B}\right)=\mathrm{d}\left(\mathrm{x},\mathrm{y}\right) \\ $$$$\mathrm{then}\:\rho\left(\mathrm{A},\mathrm{B}\right)\:\mathrm{is}\:\mathrm{the}\:\mathrm{distance}\:\mathrm{between} \\ $$$$\mathrm{two}\:\:\mathrm{points}\:\mathrm{A}\:\mathrm{and}\:\mathrm{B}\:\mathrm{of}\:\mathrm{R}^{\mathrm{2}} \left(\boldsymbol{\mathrm{q}}.\boldsymbol{\mathrm{e}}.\boldsymbol{\mathrm{d}}\right)\: \\ $$$$\left.\mathrm{b}\right)\mathrm{Suppose}\:\mathrm{A}\left(\mathrm{x}\right),\mathrm{B}\left(\mathrm{y}\right),\mathrm{C}\left(\mathrm{z}\right)\:\mathrm{are}\:\mathrm{three} \\ $$$$\mathrm{arbitrary}\:\mathrm{points}\:\mathrm{which}\:\mathrm{aren}'\mathrm{t}\:\mathrm{colinear} \\ $$$$\mathrm{We}\:\mathrm{will}\:\mathrm{prove}\:\mathrm{that}\: \\ $$$$\mathrm{d}\left(\mathrm{x},\mathrm{y}\right)+\mathrm{d}\left(\mathrm{x},\mathrm{z}\right)>\mathrm{d}\left(\mathrm{y},\mathrm{z}\right)\Leftrightarrow\mathrm{ln}\left(\mathrm{1}+\frac{\mid\mathrm{x}−\mathrm{y}\mid}{\mathrm{1}+\mid\mathrm{x}−\mathrm{y}\mid}\right) \\ $$$$+\mathrm{ln}\left(\mathrm{1}+\frac{\mid\mathrm{x}−\mathrm{z}\mid}{\mathrm{1}+\mid\mathrm{x}−\mathrm{z}\mid}\right)>\mathrm{ln}\left(\mathrm{2}+\frac{\mid\mathrm{y}−\mathrm{z}\mid}{\mathrm{1}+\mid\mathrm{y}−\mathrm{z}\mid}\right) \\ $$$$\Leftrightarrow\left(\mathrm{1}+\frac{\mid\mathrm{x}−\mathrm{y}\mid}{\mathrm{1}+\mid\mathrm{x}−\mathrm{y}\mid}\right)\left(\mathrm{1}+\frac{\mid\mathrm{x}−\mathrm{z}\mid}{\mathrm{1}+\mid\mathrm{x}−\mathrm{z}\mid}\right)> \\ $$$$\left(\mathrm{1}+\frac{\mid\mathrm{y}−\mathrm{z}\mid}{\mathrm{1}+\mid\mathrm{y}−\mathrm{z}\mid}\right)\left(\mathrm{1}\right).\mathrm{Indeed}, \\ $$$$\left(\mathrm{1}\right)\Leftrightarrow\mathrm{1}+\frac{\mid\mathrm{x}−\mathrm{y}\mid}{\mathrm{1}+\mid\mathrm{x}−\mathrm{y}\mid}+\frac{\mid\mathrm{x}−\mathrm{z}\mid}{\mathrm{1}+\mid\mathrm{x}−\mathrm{z}\mid} \\ $$$$+\frac{\mid\mathrm{x}−\mathrm{y}\mid\mid\mathrm{x}−\mathrm{z}\mid}{\left(\mathrm{1}+\mid\mathrm{x}−\mathrm{y}\mid\right)\left(\mathrm{1}+\mid\mathrm{x}−\mathrm{z}\mid\right)}>\mathrm{1}+\frac{\mid\mathrm{y}−\mathrm{z}\mid}{\mathrm{1}+\mid\mathrm{y}−\mathrm{z}\mid} \\ $$$$\Leftrightarrow\frac{\mid\mathrm{x}−\mathrm{y}\mid}{\mathrm{1}+\mid\mathrm{x}−\mathrm{y}\mid}+\frac{\mid\mathrm{x}−\mathrm{z}\mid}{\mathrm{1}+\mid\mathrm{x}−\mathrm{z}\mid} \\ $$$$\frac{\mid\mathrm{x}−\mathrm{y}\mid\mid\mathrm{x}−\mathrm{z}\mid}{\left(\mathrm{1}+\mid\mathrm{x}−\mathrm{y}\mid\right)\left(\mathrm{1}+\mid\mathrm{x}−\mathrm{z}\mid\right)}>\frac{\mid\mathrm{y}−\mathrm{z}\mid}{\mathrm{1}+\mid\mathrm{y}−\mathrm{z}\mid}=\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\mid\mathrm{y}−\mathrm{z}\mid}} \\ $$$$\bullet\mathrm{The}\:\mathrm{case}\:\mid\mathrm{y}−\mathrm{z}\mid=\mathrm{min}\left\{\mid\mid\mathrm{x}−\mathrm{y}\mid,\mid\mathrm{x}−\mathrm{z}\mid,\mid\mathrm{y}−\mathrm{z}\mid\right\} \\ $$$$\Rightarrow\frac{\mid\mathrm{x}−\mathrm{y}\mid}{\mathrm{1}+\mid\mathrm{x}−\mathrm{y}\mid}=\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\mid\mathrm{x}−\mathrm{y}\mid}}\geqslant\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\mid\mathrm{y}−\mathrm{z}\mid}} \\ $$$$\Rightarrow\mathrm{L}.\mathrm{H}.\mathrm{S}>\mathrm{R}.\mathrm{H}.\mathrm{S}\left(\boldsymbol{\mathrm{q}}.\boldsymbol{\mathrm{e}}.\boldsymbol{\mathrm{d}}\right) \\ $$$$\bullet\mathrm{The}\:\mathrm{case}\:\mid\mathrm{y}−\mathrm{z}\mid=\mathrm{max}\left\{\mid\mid\mathrm{x}−\mathrm{y}\mid,\mid\mathrm{x}−\mathrm{z}\mid,\mid\mathrm{y}−\mathrm{z}\mid\right\} \\ $$$$\Rightarrow\frac{\mid\mathrm{x}−\mathrm{y}\mid}{\mathrm{1}+\mid\mathrm{x}−\mathrm{y}\mid}+\frac{\mid\mathrm{x}−\mathrm{z}\mid}{\mathrm{1}+\mid\mathrm{x}−\mathrm{z}\mid}\geqslant\frac{\mid\mathrm{x}−\mathrm{y}\mid+\mid\mathrm{x}−\mathrm{z}\mid}{\mathrm{1}+\mathrm{max}\left\{\mid\mathrm{x}−\mathrm{y}\mid,\mid\mathrm{x}−\mathrm{z}\mid\right\}} \\ $$$$\geqslant\frac{\mid\mathrm{y}−\mathrm{z}\mid}{\mathrm{1}+\mathrm{max}\left\{\mid\mathrm{x}−\mathrm{y}\mid,\mid\mathrm{x}−\mathrm{z}\mid\right\}}\geqslant\frac{\mid\mathrm{y}−\mathrm{z}\mid}{\mathrm{1}+\mid\mathrm{y}−\mathrm{z}\mid} \\ $$$$\Rightarrow\mathrm{L}.\mathrm{H}.\mathrm{S}>\mathrm{R}.\mathrm{H}.\mathrm{S}\left(\boldsymbol{\mathrm{q}}.\boldsymbol{\mathrm{e}}.\boldsymbol{\mathrm{d}}\right) \\ $$$$\mathrm{Thus},\mathrm{in}\:\mathrm{every}\:\mathrm{cases}\:\mathrm{we}\:\mathrm{always}\:\mathrm{have} \\ $$$$\Rightarrow\mathrm{L}.\mathrm{H}.\mathrm{S}>\mathrm{R}.\mathrm{H}.\mathrm{S}.\mathrm{Therefore},\mathrm{the} \\ $$$$\mathrm{trianglar}\:\mathrm{inequality}\:\mathrm{is}\:\mathrm{proved} \\ $$
