Question Number 36192 by prof Abdo imad last updated on 30/May/18
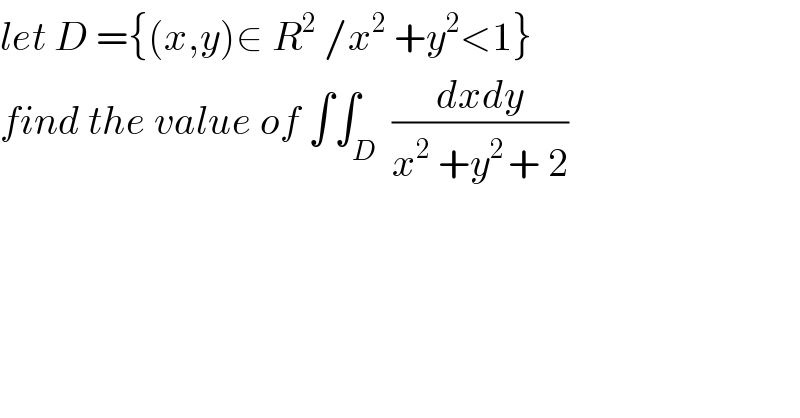
$${let}\:{D}\:=\left\{\left({x},{y}\right)\in\:{R}^{\mathrm{2}} \:/{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} <\mathrm{1}\right\} \\ $$$${find}\:{the}\:{value}\:{of}\:\int\int_{{D}} \:\frac{{dxdy}}{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}\:} +\:\mathrm{2}} \\ $$
Commented by abdo imad last updated on 31/May/18
![let consider the diffeomorphism (r,θ)→(x,y) / x =r cosθ and y =r sinθ we have ∫∫_D ((dxdy)/(x^2 +y^2 +2)) =∫∫_(0<r<1 and 0≤θ≤2π) ((r drdθ)/(r^2 +2)) =∫_0 ^1 ((rdr)/(r^2 +2)) .∫_0 ^(2π) dθ =2π [(1/2)ln(r^2 +2)]_0 ^1 =π {ln(3)−ln(2)}.](https://www.tinkutara.com/question/Q36318.png)
$${let}\:{consider}\:{the}\:{diffeomorphism}\:\left({r},\theta\right)\rightarrow\left({x},{y}\right)\:/ \\ $$$${x}\:={r}\:{cos}\theta\:\:\:{and}\:{y}\:={r}\:{sin}\theta\:\:{we}\:{have} \\ $$$$\int\int_{{D}} \frac{{dxdy}}{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} +\mathrm{2}}\:=\int\int_{\mathrm{0}<{r}<\mathrm{1}\:{and}\:\mathrm{0}\leqslant\theta\leqslant\mathrm{2}\pi} \frac{{r}\:{drd}\theta}{{r}^{\mathrm{2}} \:+\mathrm{2}} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{rdr}}{{r}^{\mathrm{2}} \:+\mathrm{2}}\:.\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:{d}\theta\:=\mathrm{2}\pi\:\left[\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({r}^{\mathrm{2}} \:+\mathrm{2}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\pi\:\left\{{ln}\left(\mathrm{3}\right)−{ln}\left(\mathrm{2}\right)\right\}. \\ $$
