Question Number 36191 by prof Abdo imad last updated on 30/May/18
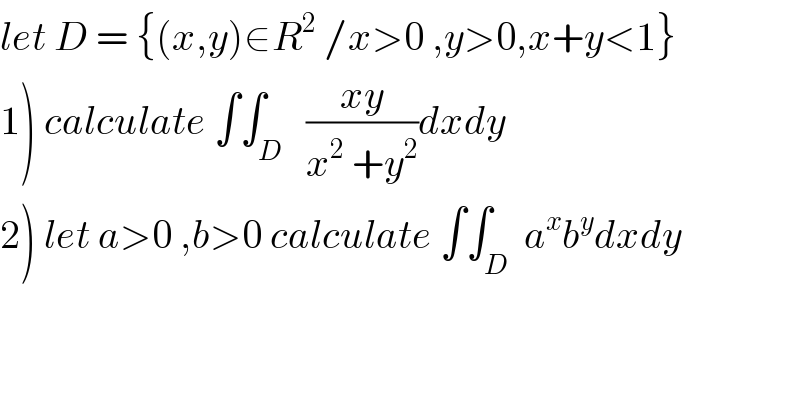
$${let}\:{D}\:=\:\left\{\left({x},{y}\right)\in{R}^{\mathrm{2}} \:/{x}>\mathrm{0}\:,{y}>\mathrm{0},{x}+{y}<\mathrm{1}\right\} \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:\int\int_{{D}} \:\:\frac{{xy}}{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} }{dxdy} \\ $$$$\left.\mathrm{2}\right)\:{let}\:{a}>\mathrm{0}\:,{b}>\mathrm{0}\:{calculate}\:\int\int_{{D}} \:{a}^{{x}} {b}^{{y}} {dxdy} \\ $$
Commented by maxmathsup by imad last updated on 26/Aug/18
![polar coordinates changement x =rcosθ and y =rsinθ x>0 and y>0 ⇒ 0<θ<(π/2) and x+y <1 ⇒ r(cosθ +sinθ)<1 ⇒ 0<r<(1/(cosθ +sinθ)) ∫∫_D ((xy)/(x^2 +y^2 ))dxdy = ∫_0 ^(π/2) (∫_0 ^(1/(cosθ+sinθ)) ((r^2 cosθsinθ)/r^2 ) rdr)dθ =∫_0 ^(π/2) ( ∫_0 ^(1/(cosθ +sinθ)) rdr)cosθ sinθ dθ but ∫_0 ^(1/(cosθ +sinθ)) rdr =[(r^2 /2)]_0 ^(1/(cosθ +sinθ)) =(1/(2(cosθ +sinθ)^2 )) =(1/(2(1+2sinθ cosθ))) ⇒ I = ∫_0 ^(π/2) ((cosθ sinθ)/(2(1+2sinθ cosθ)))dθ =(1/4) ∫_0 ^(π/2) ((sin(2θ))/(1+sin(2θ)))dθ =_(2θ =t) (1/4) ∫_0 ^π ((sint)/(1+sint)) (dt/2) =(1/8) ∫_0 ^π ((1+sint −1)/(1+sint))dt =(π/8) −(1/8) ∫_0 ^π (dt/(1+sint)) chang. tan((t/2)) =u give ∫_0 ^π (dt/(1+sint)) = ∫_0 ^∞ (1/(1+((2u)/(1+u^2 )))) ((2du)/(1+u^2 )) =2 ∫_0 ^∞ (du/(1+u^2 +2u)) =2 ∫_0 ^∞ (du/((u+1)^2 )) =2[−(1/(u+1))]_0 ^(+∞) = 2 ⇒ I =(π/8) −(1/4) .](https://www.tinkutara.com/question/Q42485.png)
$${polar}\:{coordinates}\:{changement}\:{x}\:={rcos}\theta\:\:{and}\:{y}\:={rsin}\theta\:\: \\ $$$${x}>\mathrm{0}\:{and}\:{y}>\mathrm{0}\:\Rightarrow\:\mathrm{0}<\theta<\frac{\pi}{\mathrm{2}}\:\:{and}\:{x}+{y}\:<\mathrm{1}\:\Rightarrow\:{r}\left({cos}\theta\:+{sin}\theta\right)<\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{0}<{r}<\frac{\mathrm{1}}{{cos}\theta\:+{sin}\theta} \\ $$$$\int\int_{{D}} \frac{{xy}}{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} }{dxdy}\:\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\left(\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{{cos}\theta+{sin}\theta}} \frac{{r}^{\mathrm{2}} {cos}\theta{sin}\theta}{{r}^{\mathrm{2}} }\:{rdr}\right){d}\theta \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\left(\:\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{{cos}\theta\:+{sin}\theta}} {rdr}\right){cos}\theta\:{sin}\theta\:{d}\theta\:\:\:{but} \\ $$$$\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{{cos}\theta\:+{sin}\theta}} \:{rdr}\:=\left[\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\right]_{\mathrm{0}} ^{\frac{\mathrm{1}}{{cos}\theta\:+{sin}\theta}} \:=\frac{\mathrm{1}}{\mathrm{2}\left({cos}\theta\:+{sin}\theta\right)^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+\mathrm{2}{sin}\theta\:{cos}\theta\right)}\:\Rightarrow \\ $$$${I}\:\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\frac{{cos}\theta\:{sin}\theta}{\mathrm{2}\left(\mathrm{1}+\mathrm{2}{sin}\theta\:{cos}\theta\right)}{d}\theta\:=\frac{\mathrm{1}}{\mathrm{4}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{sin}\left(\mathrm{2}\theta\right)}{\mathrm{1}+{sin}\left(\mathrm{2}\theta\right)}{d}\theta \\ $$$$=_{\mathrm{2}\theta\:={t}} \:\:\:\:\frac{\mathrm{1}}{\mathrm{4}}\:\int_{\mathrm{0}} ^{\pi} \:\:\:\:\frac{{sint}}{\mathrm{1}+{sint}}\:\frac{{dt}}{\mathrm{2}}\:=\frac{\mathrm{1}}{\mathrm{8}}\:\int_{\mathrm{0}} ^{\pi} \:\:\frac{\mathrm{1}+{sint}\:−\mathrm{1}}{\mathrm{1}+{sint}}{dt} \\ $$$$=\frac{\pi}{\mathrm{8}}\:\:−\frac{\mathrm{1}}{\mathrm{8}}\:\int_{\mathrm{0}} ^{\pi} \:\:\:\:\frac{{dt}}{\mathrm{1}+{sint}}\:\:{chang}.\:{tan}\left(\frac{{t}}{\mathrm{2}}\right)\:={u}\:{give} \\ $$$$\int_{\mathrm{0}} ^{\pi} \:\:\:\:\frac{{dt}}{\mathrm{1}+{sint}}\:\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }}\:\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} }\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{du}}{\mathrm{1}+{u}^{\mathrm{2}} \:+\mathrm{2}{u}} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{{du}}{\left({u}+\mathrm{1}\right)^{\mathrm{2}} }\:=\mathrm{2}\left[−\frac{\mathrm{1}}{{u}+\mathrm{1}}\right]_{\mathrm{0}} ^{+\infty} \:=\:\mathrm{2}\:\:\Rightarrow\:{I}\:=\frac{\pi}{\mathrm{8}}\:−\frac{\mathrm{1}}{\mathrm{4}}\:. \\ $$$$ \\ $$
