Question Number 92407 by mathmax by abdo last updated on 06/May/20
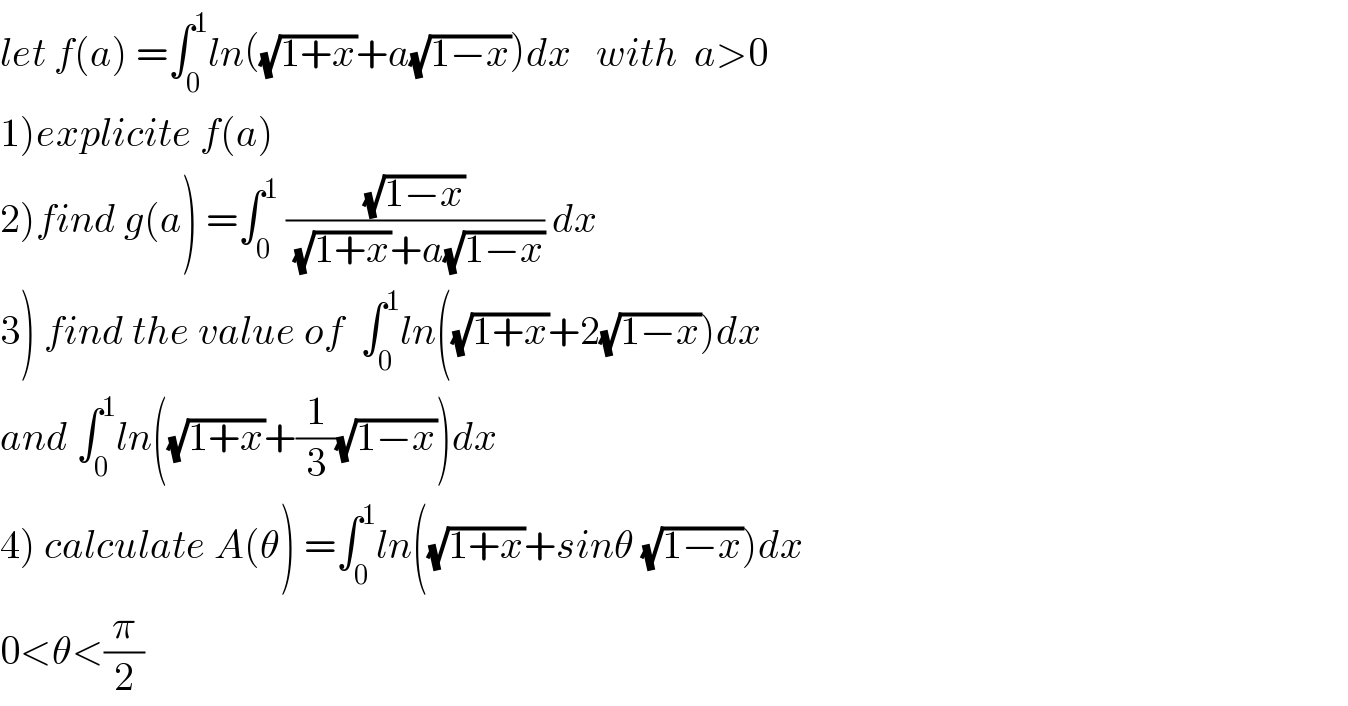
$${let}\:{f}\left({a}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\sqrt{\mathrm{1}+{x}}+{a}\sqrt{\mathrm{1}−{x}}\right){dx}\:\:\:{with}\:\:{a}>\mathrm{0} \\ $$$$\left.\mathrm{1}\right){explicite}\:{f}\left({a}\right) \\ $$$$\left.\mathrm{2}\right){find}\:{g}\left({a}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\sqrt{\mathrm{1}−{x}}}{\:\sqrt{\mathrm{1}+{x}}+{a}\sqrt{\mathrm{1}−{x}}}\:{dx} \\ $$$$\left.\mathrm{3}\right)\:{find}\:{the}\:{value}\:{of}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\sqrt{\mathrm{1}+{x}}+\mathrm{2}\sqrt{\mathrm{1}−{x}}\right){dx} \\ $$$${and}\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\sqrt{\mathrm{1}+{x}}+\frac{\mathrm{1}}{\mathrm{3}}\sqrt{\mathrm{1}−{x}}\right){dx} \\ $$$$\left.\mathrm{4}\right)\:{calculate}\:{A}\left(\theta\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\sqrt{\mathrm{1}+{x}}+{sin}\theta\:\sqrt{\mathrm{1}−{x}}\right){dx}\: \\ $$$$\mathrm{0}<\theta<\frac{\pi}{\mathrm{2}} \\ $$
