Menu Close

let-f-a-0-cos-x-2-sin-x-2-x-2-a-2-2-dx-with-a-gt-0-1-calculate-f-a-2-find-the-values-of-0-cos-x-2-sin-x-2-x-2-1-2-dx-and-0-cos-x-2-sin-x-2-

Tinku Tara 0 Comments
Pin




Question Number 64970 by mathmax by abdo last updated on 23/Jul/19
let f(a)=∫_0 ^∞ ((cos(x^2 ) +sin(x^2 ))/((x^2 +a^2 )^2 )) dx with a>0 1) calculate f(a) 2) find the values of ∫_0 ^∞ ((cos(x^2 )+sin(x^2 ))/((x^2 +1)^2 ))dx and ∫_0 ^∞ ((cos(x^2 )+sin(x^2 ))/((x^2 +3)^2 ))dx
$${let}\:{f}\left({a}\right)=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{cos}\left({x}^{\mathrm{2}} \right)\:+{sin}\left({x}^{\mathrm{2}} \right)}{\left({x}^{\mathrm{2}} \:+{a}^{\mathrm{2}} \right)^{\mathrm{2}} }\:{dx}\:\:\:{with}\:{a}>\mathrm{0} \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:{f}\left({a}\right) \\ $$$$\left.\mathrm{2}\right)\:{find}\:{the}\:{values}\:{of}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{cos}\left({x}^{\mathrm{2}} \right)+{sin}\left({x}^{\mathrm{2}} \right)}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dx}\:{and} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\frac{{cos}\left({x}^{\mathrm{2}} \right)+{sin}\left({x}^{\mathrm{2}} \right)}{\left({x}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{2}} }{dx} \\ $$
Commented by ~ À ® @ 237 ~ last updated on 23/Jul/19
we always have cos(x^2 )+sin(x^2 )=1 so f(a)=∫_0 ^∞ (1/((x^2 +a^2 )^2 ))dx let change x =a.tant dx =a (1+tan^2 t)dt f(a) = ∫_0 ^(π/2) ((a(1+tan^2 t)dt)/((a^2 tan^2 t +a^2 )^2 )) =(1/a^3 ) ∫_0 ^(π/2) (1/((1+tan^2 t)))dt =(1/a^3 ) ∫_(0 ) ^(π/2) cos^2 t dt knowing that cos^2 t = ((1+cos2t)/2) we finally got f(a)= (1/a^3 ) [(t/2) +(1/4)sin2t]_0 ^(π/2) = (π/(4a^3 )) then f(1) = (π/4) and f((√3)) = (π/(12(√3)))
$$ \\ $$$$\:\:\:\:{we}\:\:{always}\:{have}\:\:{cos}\left({x}^{\mathrm{2}} \right)+{sin}\left({x}^{\mathrm{2}} \right)=\mathrm{1} \\ $$$${so}\:\:{f}\left({a}\right)=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\left({x}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx} \\ $$$${let}\:{change}\:\:{x}\:={a}.{tant}\:\:\:\:\:\:\:\:{dx}\:={a}\:\left(\mathrm{1}+{tan}^{\mathrm{2}} {t}\right){dt} \\ $$$$\:\:\:{f}\left({a}\right)\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{a}\left(\mathrm{1}+{tan}^{\mathrm{2}} {t}\right){dt}}{\left({a}^{\mathrm{2}} {tan}^{\mathrm{2}} {t}\:+{a}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{{a}^{\mathrm{3}} }\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{\left(\mathrm{1}+{tan}^{\mathrm{2}} {t}\right)}{dt} \\ $$$$\:\:\:\:\:\:\:=\frac{\mathrm{1}}{{a}^{\mathrm{3}} }\:\int_{\mathrm{0}\:\:\:} ^{\frac{\pi}{\mathrm{2}}} {cos}^{\mathrm{2}} {t}\:\:{dt}\: \\ $$$${knowing}\:{that}\:\:{cos}^{\mathrm{2}} {t}\:\:=\:\:\frac{\mathrm{1}+{cos}\mathrm{2}{t}}{\mathrm{2}}\:\:\:{we}\:\:{finally}\:\:{got} \\ $$$$\:\:\:\:{f}\left({a}\right)=\:\frac{\mathrm{1}}{{a}^{\mathrm{3}} }\:\left[\frac{{t}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{4}}{sin}\mathrm{2}{t}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$\:\:\:\:\:\:\:\:=\:\:\frac{\pi}{\mathrm{4}{a}^{\mathrm{3}} } \\ $$$${then}\:\:\:{f}\left(\mathrm{1}\right)\:=\:\frac{\pi}{\mathrm{4}}\:\:\:\:\:\:{and}\:\:{f}\left(\sqrt{\mathrm{3}}\right)\:=\:\frac{\pi}{\mathrm{12}\sqrt{\mathrm{3}}} \\ $$
Commented by mathmax by abdo last updated on 23/Jul/19
thank you sir.
$${thank}\:{you}\:{sir}. \\ $$
Commented by mathmax by abdo last updated on 23/Jul/19
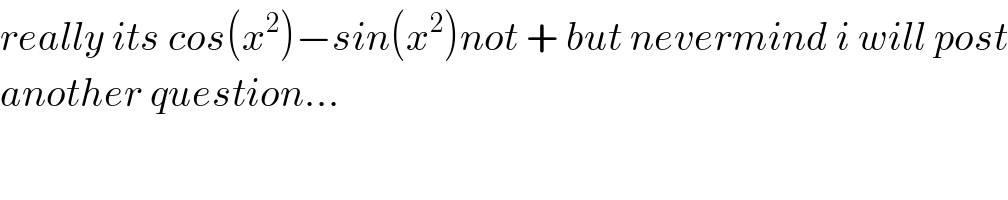
really its cos(x^2 )−sin(x^2 )not + but nevermind i will post another question...
$${really}\:{its}\:{cos}\left({x}^{\mathrm{2}} \right)−{sin}\left({x}^{\mathrm{2}} \right){not}\:+\:{but}\:{nevermind}\:{i}\:{will}\:{post} \\ $$$${another}\:{question}… \\ $$
Commented by MJS last updated on 24/Jul/19
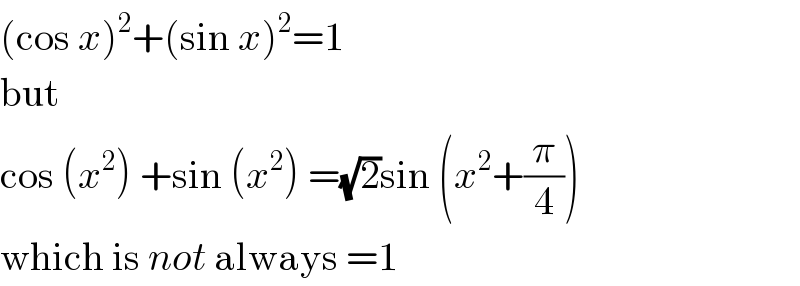
(cos x)^2 +(sin x)^2 =1 but cos (x^2 ) +sin (x^2 ) =(√2)sin (x^2 +(π/4)) which is not always =1
$$\left(\mathrm{cos}\:{x}\right)^{\mathrm{2}} +\left(\mathrm{sin}\:{x}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\mathrm{but} \\ $$$$\mathrm{cos}\:\left({x}^{\mathrm{2}} \right)\:+\mathrm{sin}\:\left({x}^{\mathrm{2}} \right)\:=\sqrt{\mathrm{2}}\mathrm{sin}\:\left({x}^{\mathrm{2}} +\frac{\pi}{\mathrm{4}}\right) \\ $$$$\mathrm{which}\:\mathrm{is}\:{not}\:\mathrm{always}\:=\mathrm{1} \\ $$
Commented by mathmax by abdo last updated on 24/Jul/19
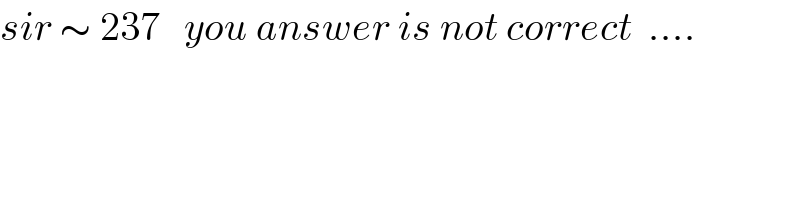
sir ∼ 237 you answer is not correct ....
$${sir}\:\sim\:\mathrm{237}\:\:\:{you}\:{answer}\:{is}\:{not}\:{correct}\:\:…. \\ $$
Commented by mathmax by abdo last updated on 24/Jul/19
you are right sir i have commited a error i delet this post and give the right answer ...
$${you}\:{are}\:{right}\:{sir}\:\:{i}\:{have}\:{commited}\:{a}\:{error}\:{i}\:{delet}\:{this}\:{post}\: \\ $$$${and}\:{give}\:{the}\:{right}\:{answer}\:… \\ $$
Commented by mathmax by abdo last updated on 24/Jul/19
1)we have cos(x^2 )+sin(x^2 ) =(√2)cos(x^2 −(π/4)) ⇒ f(a) =(√2)∫_0 ^∞ ((cos(x^2 −(π/4)))/((x^2 +a^2 )^2 ))dx ⇒2f(a) =(√2)∫_(−∞) ^(+∞) ((cos(x^2 −(π/4)))/((x^2 +a^2 )^2 ))dx ⇒(√2)f(a) =Re(∫_(−∞) ^(+∞) (e^(i(x^2 −(π/4))) /((x^2 +a^2 )^2 ))ex) let ϕ(z) =(e^(i(z^2 −(π/4))) /((z^2 +a^2 )^2 )) ⇒ ϕ(z) =(e^(i(z^2 −(π/4))) /((z−ia)^2 (z+ia)^2 )) the poles of ϕ are +^− ia (a>0) residus theorem give ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ Res(ϕ,ia) Res(ϕ,ia) =lim_(z→ia) (z−ia)^2 {(z−ia)^2 ϕ(z)}^((1)) =lim_(z→ia) {(e^(i(z^2 −(π/4))) /((z+ia)^2 ))}^((1)) =e^(−((iπ)/4)) lim_(z→ia) {(e^(iz^2 ) /((z+ia)^2 ))}^((1)) =e^(−((iπ)/4)) lim_(z→ia) ((2iz e^(iz^2 ) (z+ia)^2 −2(z+ia)e^(iz^2 ) )/((z+ia)^4 )) =e^(−((iπ)/4)) lim_(z→ia) (((2iz(z+ia)−2)e^(iz^2 ) )/((z+ia)^3 )) =e^(−i(π/4)) ((2i(ia)(2ia)−2)/((2ia)^3 )) e^(i(ia)^2 ) = e^(−((iπ)/4)) ((−4ia^2 −2)/(−8ia^3 )) e^(−ia^2 ) =((2ia^2 −1)/(4ia^3 )) e^(−i((π/4)+a^2 )) ⇒∫_(−∞) ^(+∞) ϕ(z)dz =2iπ ((2ia^2 −1)/(4ia^3 )) e^(−i((π/4)+a^2 )) =−(π/(2a^3 ))(1−2ia^2 )( cos((π/4)+a^2 )−isin((π/4)+a^2 )) =−(π/(2a^3 )){cos((π/4)+a^2 )−isin((π/4)+a^2 )−2ia^2 cos((π/4)+a^2 )−2a^2 sin((π/4)+a^2 )} (√2)f(a) =−(π/(2a^3 ))(cos((π/4)+a^2 )−2a^2 sin((π/4) +a^2 )) =−(π/(2a^3 ))cos((π/4)+a^2 ) +(π/a) sin((π/4) +a^2 ) ⇒ f(a) =(π/(a(√2)))sin((π/4) +a^2 )−(π/(2(√2)a^3 )) cos((π/4) +a^2 )
$$\left.\mathrm{1}\right){we}\:{have}\:{cos}\left({x}^{\mathrm{2}} \right)+{sin}\left({x}^{\mathrm{2}} \right)\:=\sqrt{\mathrm{2}}{cos}\left({x}^{\mathrm{2}} −\frac{\pi}{\mathrm{4}}\right)\:\Rightarrow \\ $$$${f}\left({a}\right)\:=\sqrt{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{cos}\left({x}^{\mathrm{2}} −\frac{\pi}{\mathrm{4}}\right)}{\left({x}^{\mathrm{2}} \:+{a}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx}\:\Rightarrow\mathrm{2}{f}\left({a}\right)\:=\sqrt{\mathrm{2}}\int_{−\infty} ^{+\infty} \:\frac{{cos}\left({x}^{\mathrm{2}} −\frac{\pi}{\mathrm{4}}\right)}{\left({x}^{\mathrm{2}} \:+{a}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx} \\ $$$$\Rightarrow\sqrt{\mathrm{2}}{f}\left({a}\right)\:={Re}\left(\int_{−\infty} ^{+\infty} \:\:\frac{{e}^{{i}\left({x}^{\mathrm{2}} −\frac{\pi}{\mathrm{4}}\right)} }{\left({x}^{\mathrm{2}} \:+{a}^{\mathrm{2}} \right)^{\mathrm{2}} }{ex}\right)\:{let}\:\varphi\left({z}\right)\:=\frac{{e}^{{i}\left({z}^{\mathrm{2}} −\frac{\pi}{\mathrm{4}}\right)} }{\left({z}^{\mathrm{2}} \:+{a}^{\mathrm{2}} \right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\varphi\left({z}\right)\:=\frac{{e}^{{i}\left({z}^{\mathrm{2}} −\frac{\pi}{\mathrm{4}}\right)} }{\left({z}−{ia}\right)^{\mathrm{2}} \left({z}+{ia}\right)^{\mathrm{2}} }\:\:{the}\:{poles}\:{of}\:\varphi\:{are}\:\overset{−} {+}{ia}\:\:\left({a}>\mathrm{0}\right)\:{residus} \\ $$$${theorem}\:{give}\:\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:{Res}\left(\varphi,{ia}\right) \\ $$$${Res}\left(\varphi,{ia}\right)\:={lim}_{{z}\rightarrow{ia}} \left({z}−{ia}\right)^{\mathrm{2}} \left\{\left({z}−{ia}\right)^{\mathrm{2}} \varphi\left({z}\right)\right\}^{\left(\mathrm{1}\right)} \\ $$$$={lim}_{{z}\rightarrow{ia}} \:\:\left\{\frac{{e}^{{i}\left({z}^{\mathrm{2}} −\frac{\pi}{\mathrm{4}}\right)} }{\left({z}+{ia}\right)^{\mathrm{2}} }\right\}^{\left(\mathrm{1}\right)} \:={e}^{−\frac{{i}\pi}{\mathrm{4}}} \:{lim}_{{z}\rightarrow{ia}} \:\:\:\left\{\frac{{e}^{{iz}^{\mathrm{2}} } }{\left({z}+{ia}\right)^{\mathrm{2}} }\right\}^{\left(\mathrm{1}\right)} \\ $$$$={e}^{−\frac{{i}\pi}{\mathrm{4}}} \:\:\:{lim}_{{z}\rightarrow{ia}} \:\:\:\frac{\mathrm{2}{iz}\:{e}^{{iz}^{\mathrm{2}} } \left({z}+{ia}\right)^{\mathrm{2}} \:−\mathrm{2}\left({z}+{ia}\right){e}^{{iz}^{\mathrm{2}} } }{\left({z}+{ia}\right)^{\mathrm{4}} } \\ $$$$={e}^{−\frac{{i}\pi}{\mathrm{4}}} \:{lim}_{{z}\rightarrow{ia}} \:\:\:\:\frac{\left(\mathrm{2}{iz}\left({z}+{ia}\right)−\mathrm{2}\right){e}^{{iz}^{\mathrm{2}} } }{\left({z}+{ia}\right)^{\mathrm{3}} } \\ $$$$={e}^{−{i}\frac{\pi}{\mathrm{4}}} \:\:\frac{\mathrm{2}{i}\left({ia}\right)\left(\mathrm{2}{ia}\right)−\mathrm{2}}{\left(\mathrm{2}{ia}\right)^{\mathrm{3}} }\:{e}^{{i}\left({ia}\right)^{\mathrm{2}} } =\:{e}^{−\frac{{i}\pi}{\mathrm{4}}} \:\:\frac{−\mathrm{4}{ia}^{\mathrm{2}} −\mathrm{2}}{−\mathrm{8}{ia}^{\mathrm{3}} }\:{e}^{−{ia}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{2}{ia}^{\mathrm{2}} −\mathrm{1}}{\mathrm{4}{ia}^{\mathrm{3}} }\:{e}^{−{i}\left(\frac{\pi}{\mathrm{4}}+{a}^{\mathrm{2}} \right)} \:\Rightarrow\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:\frac{\mathrm{2}{ia}^{\mathrm{2}} −\mathrm{1}}{\mathrm{4}{ia}^{\mathrm{3}} }\:{e}^{−{i}\left(\frac{\pi}{\mathrm{4}}+{a}^{\mathrm{2}} \right)} \\ $$$$=−\frac{\pi}{\mathrm{2}{a}^{\mathrm{3}} }\left(\mathrm{1}−\mathrm{2}{ia}^{\mathrm{2}} \right)\left(\:{cos}\left(\frac{\pi}{\mathrm{4}}+{a}^{\mathrm{2}} \right)−{isin}\left(\frac{\pi}{\mathrm{4}}+{a}^{\mathrm{2}} \right)\right) \\ $$$$=−\frac{\pi}{\mathrm{2}{a}^{\mathrm{3}} }\left\{{cos}\left(\frac{\pi}{\mathrm{4}}+{a}^{\mathrm{2}} \right)−{isin}\left(\frac{\pi}{\mathrm{4}}+{a}^{\mathrm{2}} \right)−\mathrm{2}{ia}^{\mathrm{2}} {cos}\left(\frac{\pi}{\mathrm{4}}+{a}^{\mathrm{2}} \right)−\mathrm{2}{a}^{\mathrm{2}} {sin}\left(\frac{\pi}{\mathrm{4}}+{a}^{\mathrm{2}} \right)\right\} \\ $$$$\sqrt{\mathrm{2}}{f}\left({a}\right)\:=−\frac{\pi}{\mathrm{2}{a}^{\mathrm{3}} }\left({cos}\left(\frac{\pi}{\mathrm{4}}+{a}^{\mathrm{2}} \right)−\mathrm{2}{a}^{\mathrm{2}} {sin}\left(\frac{\pi}{\mathrm{4}}\:+{a}^{\mathrm{2}} \right)\right) \\ $$$$=−\frac{\pi}{\mathrm{2}{a}^{\mathrm{3}} }{cos}\left(\frac{\pi}{\mathrm{4}}+{a}^{\mathrm{2}} \right)\:+\frac{\pi}{{a}}\:{sin}\left(\frac{\pi}{\mathrm{4}}\:+{a}^{\mathrm{2}} \right)\:\Rightarrow \\ $$$${f}\left({a}\right)\:=\frac{\pi}{{a}\sqrt{\mathrm{2}}}{sin}\left(\frac{\pi}{\mathrm{4}}\:+{a}^{\mathrm{2}} \right)−\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}{a}^{\mathrm{3}} }\:{cos}\left(\frac{\pi}{\mathrm{4}}\:+{a}^{\mathrm{2}} \right) \\ $$
Commented by mathmax by abdo last updated on 24/Jul/19
2) ∫_0 ^∞ ((cos(x^2 )+sin(x^2 ))/((x^2 +1)^2 ))dx =f(1) =(π/( (√2)))sin((π/4)+1)−(π/(2(√2)))cos((π/4)+1) ∫_0 ^∞ ((cos(x^2 )+sin(x^2 ))/((x^2 +3)^2 )) =f((√3)) =(π/( (√6)))sin((π/4)+3)−(π/(2(√2)3(√3))) cos((π/4)+3) =(π/( (√6)))sin(3+(π/4))−(π/(6(√6))) cos(3+(π/4)).
$$\left.\mathrm{2}\right)\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{cos}\left({x}^{\mathrm{2}} \right)+{sin}\left({x}^{\mathrm{2}} \right)}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dx}\:={f}\left(\mathrm{1}\right)\:=\frac{\pi}{\:\sqrt{\mathrm{2}}}{sin}\left(\frac{\pi}{\mathrm{4}}+\mathrm{1}\right)−\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}}{cos}\left(\frac{\pi}{\mathrm{4}}+\mathrm{1}\right) \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{{cos}\left({x}^{\mathrm{2}} \right)+{sin}\left({x}^{\mathrm{2}} \right)}{\left({x}^{\mathrm{2}} \:+\mathrm{3}\right)^{\mathrm{2}} }\:={f}\left(\sqrt{\mathrm{3}}\right)\:=\frac{\pi}{\:\sqrt{\mathrm{6}}}{sin}\left(\frac{\pi}{\mathrm{4}}+\mathrm{3}\right)−\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}\mathrm{3}\sqrt{\mathrm{3}}}\:{cos}\left(\frac{\pi}{\mathrm{4}}+\mathrm{3}\right) \\ $$$$=\frac{\pi}{\:\sqrt{\mathrm{6}}}{sin}\left(\mathrm{3}+\frac{\pi}{\mathrm{4}}\right)−\frac{\pi}{\mathrm{6}\sqrt{\mathrm{6}}}\:{cos}\left(\mathrm{3}+\frac{\pi}{\mathrm{4}}\right). \\ $$
Commented by ~ À ® @ 237 ~ last updated on 25/Jul/19
yes you are right . I did not mind the difference at this time . Sorry
$$\:\:\:{yes}\:\:{you}\:{are}\:{right}\:.\:{I}\:{did}\:{not}\:{mind}\:{the}\:{difference}\:{at}\:{this}\:{time}\:\:.\:{Sorry} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *