Menu Close

let-f-a-0-e-ax-ln-x-dx-with-a-gt-0-1-find-f-a-2-find-0-e-ax-xlnx-dx-3-calculate-0-e-2x-xlnx-dx-

Tinku Tara 0 Comments
Pin




Question Number 32031 by abdo imad last updated on 18/Mar/18
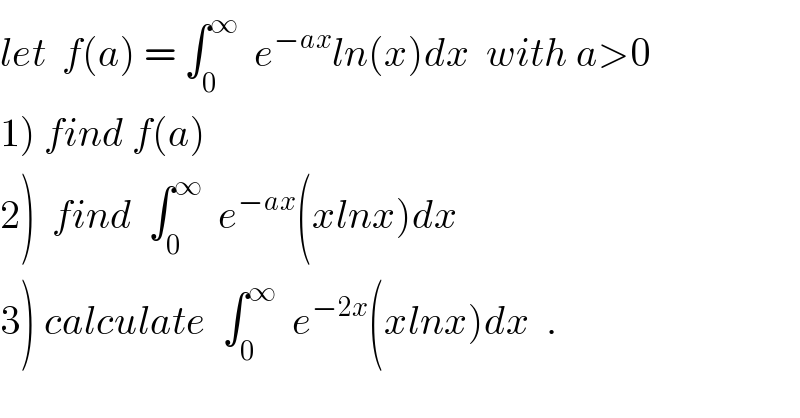
let f(a) = ∫_0 ^∞ e^(−ax) ln(x)dx with a>0 1) find f(a) 2) find ∫_0 ^∞ e^(−ax) (xlnx)dx 3) calculate ∫_0 ^∞ e^(−2x) (xlnx)dx .
$${let}\:\:{f}\left({a}\right)\:=\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{ax}} {ln}\left({x}\right){dx}\:\:{with}\:{a}>\mathrm{0} \\ $$$$\left.\mathrm{1}\right)\:{find}\:{f}\left({a}\right)\: \\ $$$$\left.\mathrm{2}\right)\:\:{find}\:\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{ax}} \left({xlnx}\right){dx} \\ $$$$\left.\mathrm{3}\right)\:{calculate}\:\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−\mathrm{2}{x}} \left({xlnx}\right){dx}\:\:. \\ $$
Commented by abdo imad last updated on 20/Mar/18
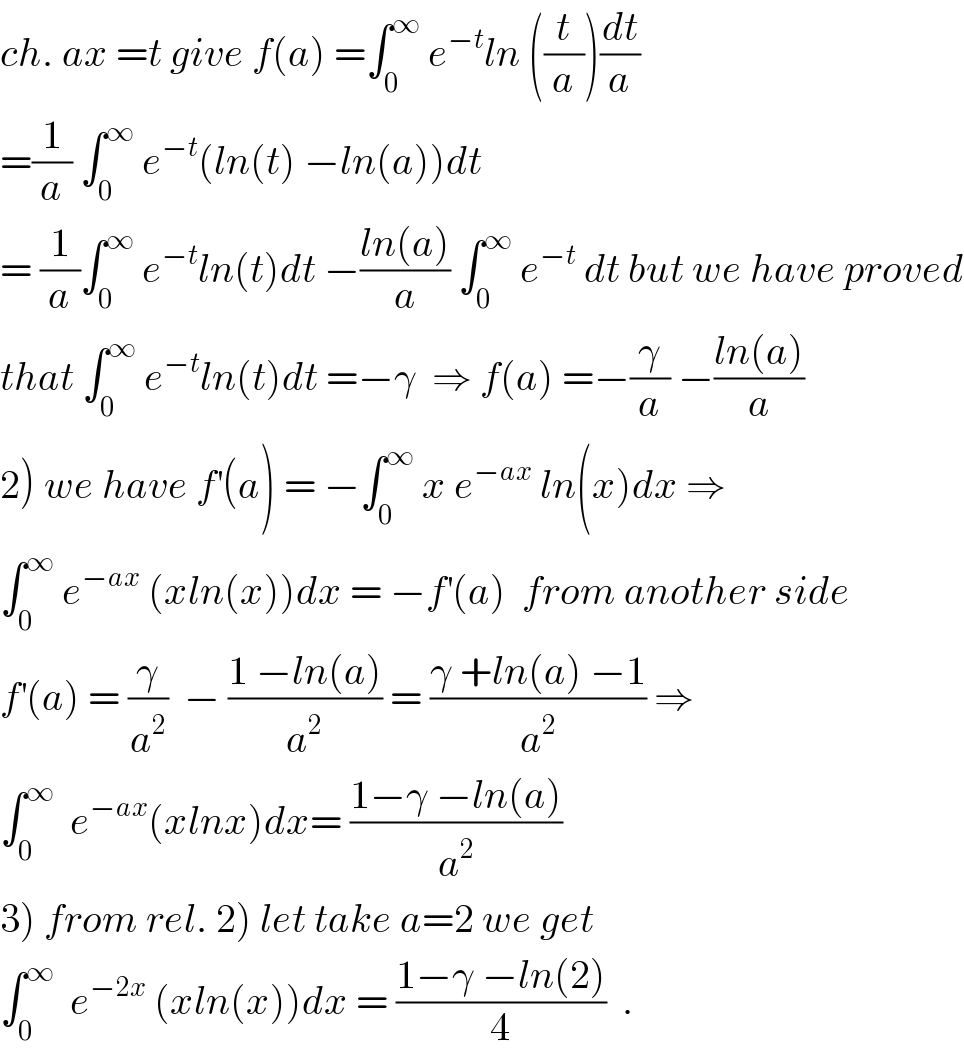
ch. ax =t give f(a) =∫_0 ^∞ e^(−t) ln ((t/a))(dt/a) =(1/a) ∫_0 ^∞ e^(−t) (ln(t) −ln(a))dt = (1/a)∫_0 ^∞ e^(−t) ln(t)dt −((ln(a))/a) ∫_0 ^∞ e^(−t) dt but we have proved that ∫_0 ^∞ e^(−t) ln(t)dt =−γ ⇒ f(a) =−(γ/a) −((ln(a))/a) 2) we have f^′ (a) = −∫_0 ^∞ x e^(−ax) ln(x)dx ⇒ ∫_0 ^∞ e^(−ax) (xln(x))dx = −f^′ (a) from another side f^′ (a) = (γ/a^2 ) − ((1 −ln(a))/a^2 ) = ((γ +ln(a) −1)/a^2 ) ⇒ ∫_0 ^∞ e^(−ax) (xlnx)dx= ((1−γ −ln(a))/a^2 ) 3) from rel. 2) let take a=2 we get ∫_0 ^∞ e^(−2x) (xln(x))dx = ((1−γ −ln(2))/4) .
$${ch}.\:{ax}\:={t}\:{give}\:{f}\left({a}\right)\:=\int_{\mathrm{0}} ^{\infty} \:{e}^{−{t}} {ln}\:\left(\frac{{t}}{{a}}\right)\frac{{dt}}{{a}} \\ $$$$=\frac{\mathrm{1}}{{a}}\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−{t}} \left({ln}\left({t}\right)\:−{ln}\left({a}\right)\right){dt}\: \\ $$$$=\:\frac{\mathrm{1}}{{a}}\int_{\mathrm{0}} ^{\infty} \:{e}^{−{t}} {ln}\left({t}\right){dt}\:−\frac{{ln}\left({a}\right)}{{a}}\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−{t}} \:{dt}\:{but}\:{we}\:{have}\:{proved} \\ $$$${that}\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−{t}} {ln}\left({t}\right){dt}\:=−\gamma\:\:\Rightarrow\:{f}\left({a}\right)\:=−\frac{\gamma}{{a}}\:−\frac{{ln}\left({a}\right)}{{a}} \\ $$$$\left.\mathrm{2}\right)\:{we}\:{have}\:{f}^{'} \left({a}\right)\:=\:−\int_{\mathrm{0}} ^{\infty} \:{x}\:{e}^{−{ax}} \:{ln}\left({x}\right){dx}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:{e}^{−{ax}} \:\left({xln}\left({x}\right)\right){dx}\:=\:−{f}^{'} \left({a}\right)\:\:{from}\:{another}\:{side} \\ $$$${f}^{'} \left({a}\right)\:=\:\frac{\gamma}{{a}^{\mathrm{2}} }\:\:−\:\frac{\mathrm{1}\:−{ln}\left({a}\right)}{{a}^{\mathrm{2}} }\:=\:\frac{\gamma\:+{ln}\left({a}\right)\:−\mathrm{1}}{{a}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{ax}} \left({xlnx}\right){dx}=\:\frac{\mathrm{1}−\gamma\:−{ln}\left({a}\right)}{{a}^{\mathrm{2}} } \\ $$$$\left.\mathrm{3}\left.\right)\:{from}\:{rel}.\:\mathrm{2}\right)\:{let}\:{take}\:{a}=\mathrm{2}\:{we}\:{get} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−\mathrm{2}{x}} \:\left({xln}\left({x}\right)\right){dx}\:=\:\frac{\mathrm{1}−\gamma\:−{ln}\left(\mathrm{2}\right)}{\mathrm{4}}\:\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *