Question Number 116376 by bemath last updated on 03/Oct/20

$$\mathrm{Let}\:\mathrm{f}\:\mathrm{be}\:\mathrm{a}\:\mathrm{function}\:\mathrm{defined}\:\mathrm{on}\:\mathrm{non}\:\mathrm{zero}\:\: \\ $$$$\mathrm{real}\:\mathrm{numbers}\:\mathrm{such}\:\mathrm{that}\:\frac{\mathrm{27}\:\mathrm{f}\left(−\mathrm{x}\right)}{\mathrm{x}}\:−\mathrm{x}^{\mathrm{2}} \:\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)\:=−\mathrm{2x}^{\mathrm{2}} \\ $$$$\mathrm{for}\:\forall\mathrm{x}\:\neq\:\mathrm{0}\:.\:\mathrm{Find}\:\rightarrow\begin{cases}{\mathrm{f}\left(\mathrm{x}\right)}\\{\mathrm{f}\left(\mathrm{3}\right)}\end{cases}\:?\: \\ $$
Answered by bobhans last updated on 03/Oct/20
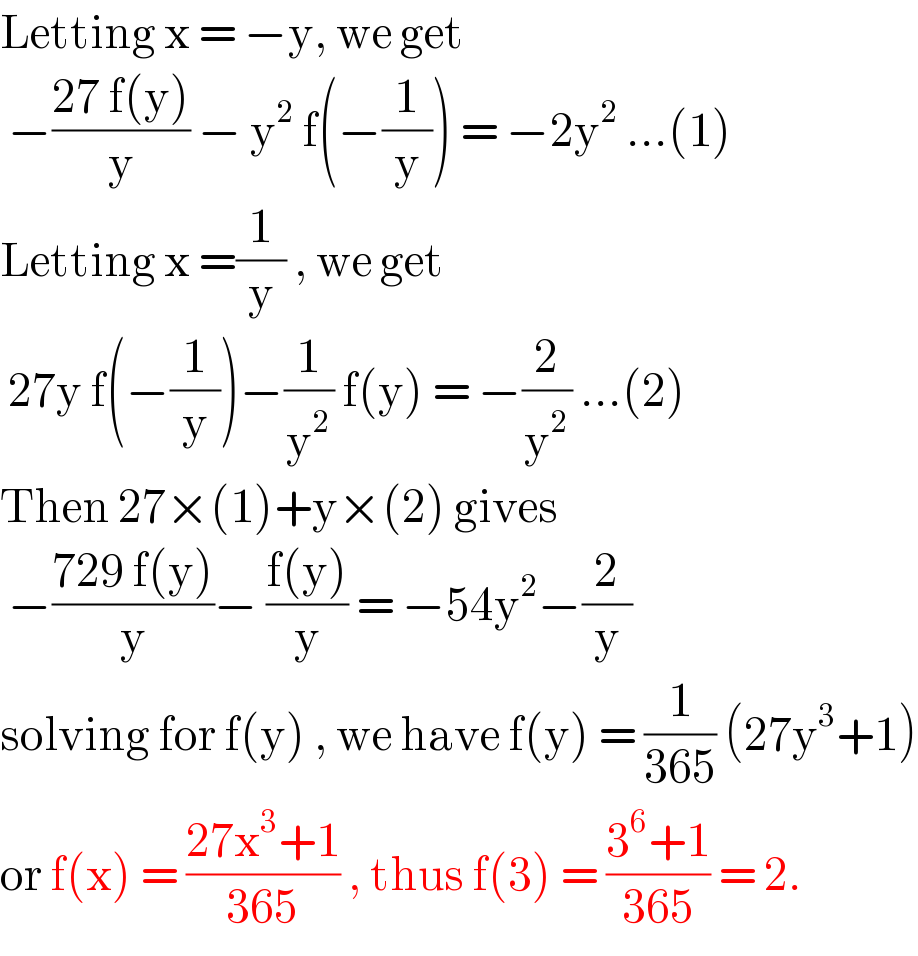
$$\mathrm{Letting}\:\mathrm{x}\:=\:−\mathrm{y},\:\mathrm{we}\:\mathrm{get}\: \\ $$$$\:−\frac{\mathrm{27}\:\mathrm{f}\left(\mathrm{y}\right)}{\mathrm{y}}\:−\:\mathrm{y}^{\mathrm{2}} \:\mathrm{f}\left(−\frac{\mathrm{1}}{\mathrm{y}}\right)\:=\:−\mathrm{2y}^{\mathrm{2}} \:…\left(\mathrm{1}\right) \\ $$$$\mathrm{Letting}\:\mathrm{x}\:=\frac{\mathrm{1}}{\mathrm{y}}\:,\:\mathrm{we}\:\mathrm{get}\: \\ $$$$\:\mathrm{27y}\:\mathrm{f}\left(−\frac{\mathrm{1}}{\mathrm{y}}\right)−\frac{\mathrm{1}}{\mathrm{y}^{\mathrm{2}} }\:\mathrm{f}\left(\mathrm{y}\right)\:=\:−\frac{\mathrm{2}}{\mathrm{y}^{\mathrm{2}} }\:…\left(\mathrm{2}\right) \\ $$$$\mathrm{Then}\:\mathrm{27}×\left(\mathrm{1}\right)+\mathrm{y}×\left(\mathrm{2}\right)\:\mathrm{gives} \\ $$$$\:−\frac{\mathrm{729}\:\mathrm{f}\left(\mathrm{y}\right)}{\mathrm{y}}−\:\frac{\mathrm{f}\left(\mathrm{y}\right)}{\mathrm{y}}\:=\:−\mathrm{54y}^{\mathrm{2}} −\frac{\mathrm{2}}{\mathrm{y}} \\ $$$$\mathrm{solving}\:\mathrm{for}\:\mathrm{f}\left(\mathrm{y}\right)\:,\:\mathrm{we}\:\mathrm{have}\:\mathrm{f}\left(\mathrm{y}\right)\:=\:\frac{\mathrm{1}}{\mathrm{365}}\:\left(\mathrm{27y}^{\mathrm{3}} +\mathrm{1}\right) \\ $$$$\mathrm{or}\:\mathrm{f}\left(\mathrm{x}\right)\:=\:\frac{\mathrm{27x}^{\mathrm{3}} +\mathrm{1}}{\mathrm{365}}\:,\:\mathrm{thus}\:\mathrm{f}\left(\mathrm{3}\right)\:=\:\frac{\mathrm{3}^{\mathrm{6}} +\mathrm{1}}{\mathrm{365}}\:=\:\mathrm{2}. \\ $$
Commented by bemath last updated on 03/Oct/20

$$\mathrm{santuyy} \\ $$
Answered by mathmax by abdo last updated on 03/Oct/20
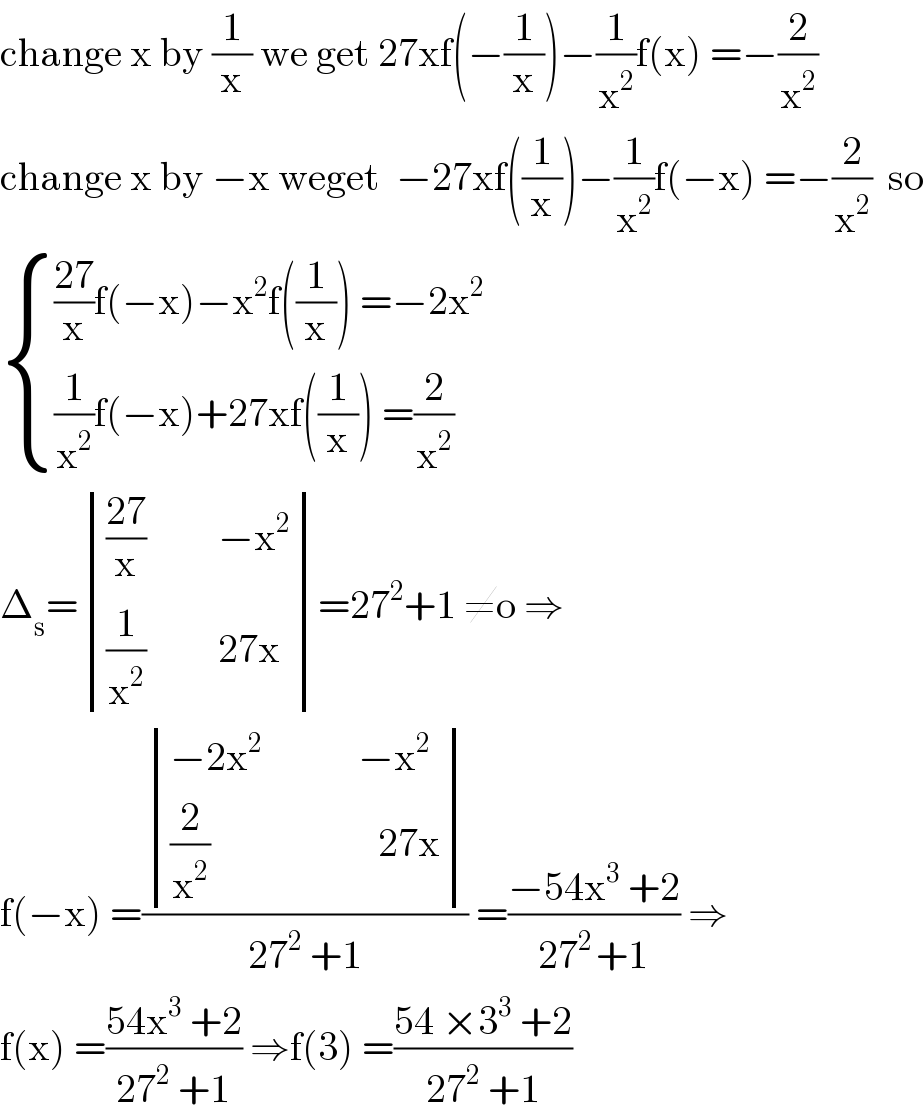
$$\mathrm{change}\:\mathrm{x}\:\mathrm{by}\:\frac{\mathrm{1}}{\mathrm{x}}\:\mathrm{we}\:\mathrm{get}\:\mathrm{27xf}\left(−\frac{\mathrm{1}}{\mathrm{x}}\right)−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\mathrm{f}\left(\mathrm{x}\right)\:=−\frac{\mathrm{2}}{\mathrm{x}^{\mathrm{2}} } \\ $$$$\mathrm{change}\:\mathrm{x}\:\mathrm{by}\:−\mathrm{x}\:\mathrm{weget}\:\:−\mathrm{27xf}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\mathrm{f}\left(−\mathrm{x}\right)\:=−\frac{\mathrm{2}}{\mathrm{x}^{\mathrm{2}} }\:\:\mathrm{so} \\ $$$$\begin{cases}{\frac{\mathrm{27}}{\mathrm{x}}\mathrm{f}\left(−\mathrm{x}\right)−\mathrm{x}^{\mathrm{2}} \mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)\:=−\mathrm{2x}^{\mathrm{2}} }\\{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\mathrm{f}\left(−\mathrm{x}\right)+\mathrm{27xf}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)\:=\frac{\mathrm{2}}{\mathrm{x}^{\mathrm{2}} }}\end{cases} \\ $$$$\Delta_{\mathrm{s}} =\begin{vmatrix}{\frac{\mathrm{27}}{\mathrm{x}}\:\:\:\:\:\:\:\:\:−\mathrm{x}^{\mathrm{2}} }\\{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\:\:\:\:\:\:\:\:\:\mathrm{27x}}\end{vmatrix}=\mathrm{27}^{\mathrm{2}} +\mathrm{1}\:\neq\mathrm{o}\:\Rightarrow \\ $$$$\mathrm{f}\left(−\mathrm{x}\right)\:=\frac{\begin{vmatrix}{−\mathrm{2x}^{\mathrm{2}} \:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{x}^{\mathrm{2}} }\\{\frac{\mathrm{2}}{\mathrm{x}^{\mathrm{2}} }\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{27x}}\end{vmatrix}}{\mathrm{27}^{\mathrm{2}} \:+\mathrm{1}}\:=\frac{−\mathrm{54x}^{\mathrm{3}} \:+\mathrm{2}}{\mathrm{27}^{\mathrm{2}\:} +\mathrm{1}}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{54x}^{\mathrm{3}} \:+\mathrm{2}}{\mathrm{27}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow\mathrm{f}\left(\mathrm{3}\right)\:=\frac{\mathrm{54}\:×\mathrm{3}^{\mathrm{3}} \:+\mathrm{2}}{\mathrm{27}^{\mathrm{2}} \:+\mathrm{1}} \\ $$
