Question Number 52499 by Joel578 last updated on 09/Jan/19
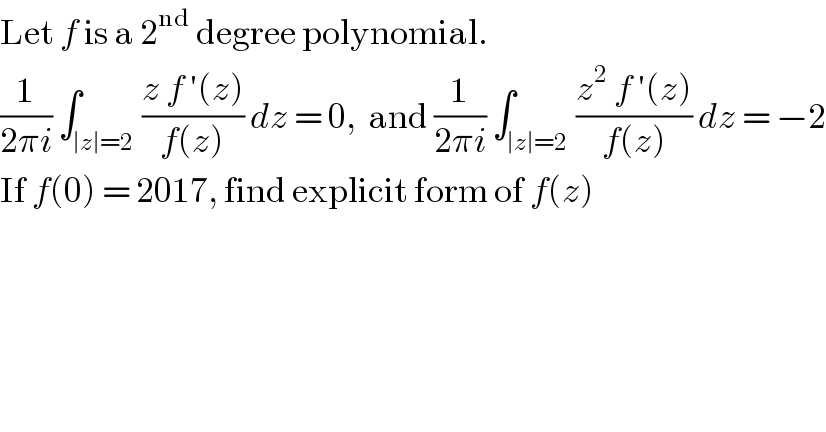
$$\mathrm{Let}\:{f}\:\mathrm{is}\:\mathrm{a}\:\mathrm{2}^{\mathrm{nd}} \:\mathrm{degree}\:\mathrm{polynomial}. \\ $$$$\frac{\mathrm{1}}{\mathrm{2}\pi{i}}\:\int_{\mid{z}\mid=\mathrm{2}} \frac{{z}\:{f}\:'\left({z}\right)}{{f}\left({z}\right)}\:{dz}\:=\:\mathrm{0},\:\:\mathrm{and}\:\frac{\mathrm{1}}{\mathrm{2}\pi{i}}\:\int_{\mid{z}\mid=\mathrm{2}} \frac{{z}^{\mathrm{2}} \:{f}\:'\left({z}\right)}{{f}\left({z}\right)}\:{dz}\:=\:−\mathrm{2} \\ $$$$\mathrm{If}\:{f}\left(\mathrm{0}\right)\:=\:\mathrm{2017},\:\mathrm{find}\:\mathrm{explicit}\:\mathrm{form}\:\mathrm{of}\:{f}\left({z}\right) \\ $$
