Question Number 33048 by rahul 19 last updated on 09/Apr/18

Commented by rahul 19 last updated on 09/Apr/18
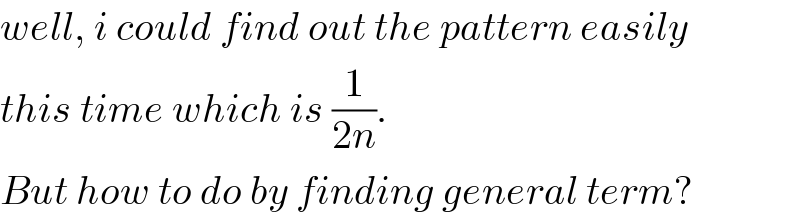
Commented by rahul 19 last updated on 09/Apr/18
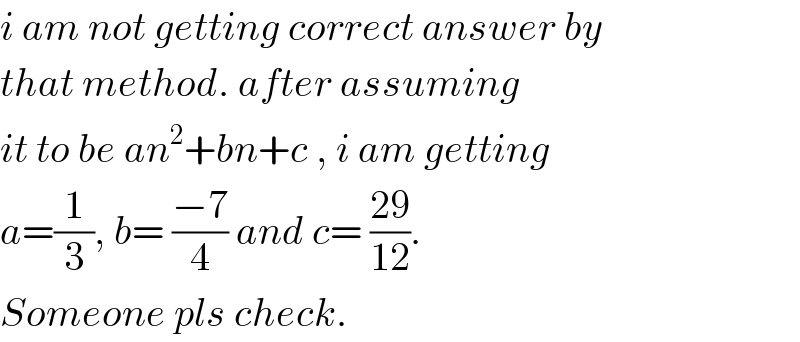
Commented by MJS last updated on 09/Apr/18
![...you already found it. the polynomial method doesn′t work with patterns like this, when you already have a formular for all n∈N i.e. if we know a_0 =1; a_1 =1; a_2 =2; a_3 =6; a_4 =24 we believe it′s n! but we can find ∞ functions satisfying these pairs (n;a_n ), one is a 4^(th) −degree polynomial if we know a_0 =1; a_n =n×a_(n−1) we know it′s n!, and there′s no polynome for it [if you find one, you′ll get the Nobel Price ;−)]](https://www.tinkutara.com/question/Q33058.png)
Commented by MJS last updated on 09/Apr/18

Commented by rahul 19 last updated on 09/Apr/18
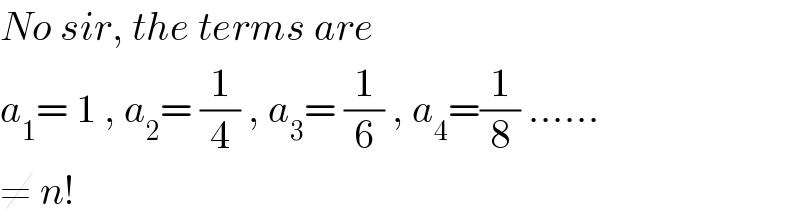
Commented by MJS last updated on 09/Apr/18

Commented by rahul 19 last updated on 09/Apr/18

