Question Number 52679 by maxmathsup by imad last updated on 11/Jan/19
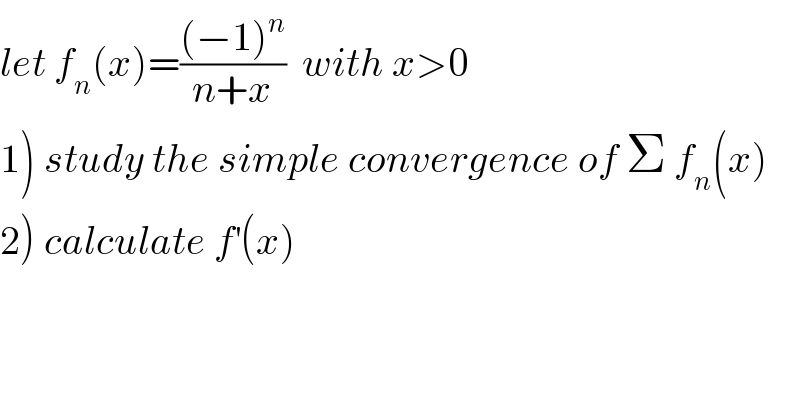
$${let}\:{f}_{{n}} \left({x}\right)=\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}+{x}}\:\:{with}\:{x}>\mathrm{0} \\ $$$$\left.\mathrm{1}\right)\:{study}\:{the}\:{simple}\:{convergence}\:{of}\:\Sigma\:{f}_{{n}} \left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:{f}^{'} \left({x}\right) \\ $$
Commented by maxmathsup by imad last updated on 28/Feb/19
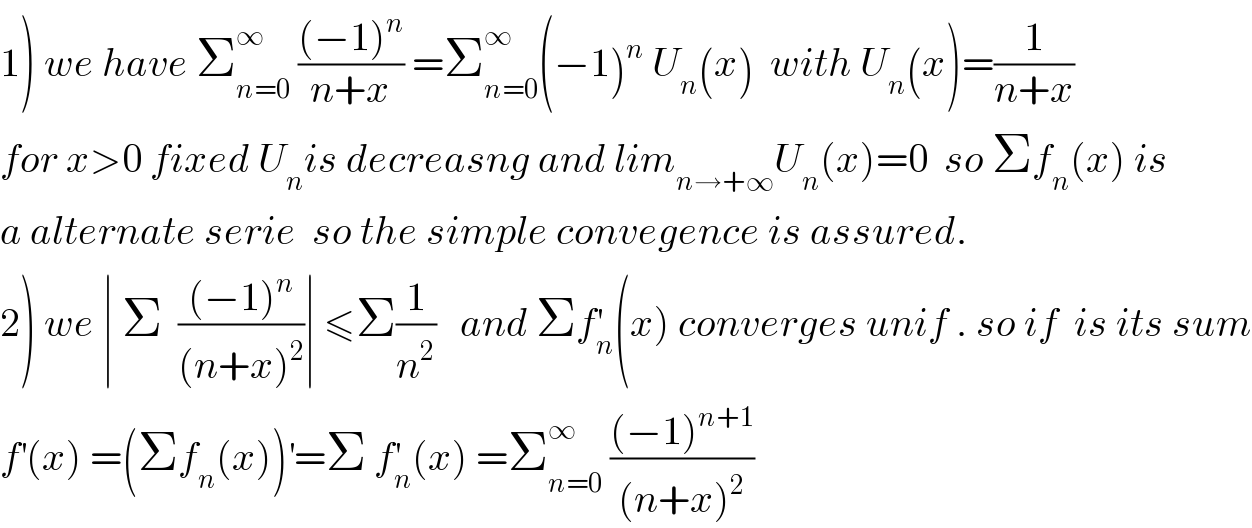
$$\left.\mathrm{1}\right)\:{we}\:{have}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}+{x}}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \:{U}_{{n}} \left({x}\right)\:\:{with}\:{U}_{{n}} \left({x}\right)=\frac{\mathrm{1}}{{n}+{x}} \\ $$$${for}\:{x}>\mathrm{0}\:{fixed}\:{U}_{{n}} {is}\:{decreasng}\:{and}\:{lim}_{{n}\rightarrow+\infty} {U}_{{n}} \left({x}\right)=\mathrm{0}\:\:{so}\:\Sigma{f}_{{n}} \left({x}\right)\:{is}\: \\ $$$${a}\:{alternate}\:{serie}\:\:{so}\:{the}\:{simple}\:{convegence}\:{is}\:{assured}. \\ $$$$\left.\mathrm{2}\right)\:{we}\:\mid\:\Sigma\:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left({n}+{x}\right)^{\mathrm{2}} }\mid\:\leqslant\Sigma\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:\:\:{and}\:\Sigma{f}_{{n}} ^{'} \left({x}\right)\:{converges}\:{unif}\:.\:{so}\:{if}\:\:{is}\:{its}\:{sum} \\ $$$${f}^{'} \left({x}\right)\:=\left(\Sigma{f}_{{n}} \left({x}\right)\right)^{'} =\Sigma\:{f}_{{n}} ^{'} \left({x}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{\left({n}+{x}\right)^{\mathrm{2}} } \\ $$
