Question Number 36690 by prof Abdo imad last updated on 04/Jun/18
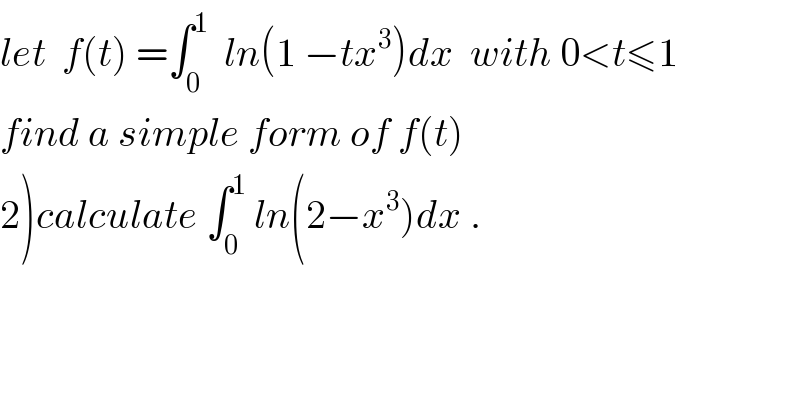
$${let}\:\:{f}\left({t}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{ln}\left(\mathrm{1}\:−{tx}^{\mathrm{3}} \right){dx}\:\:{with}\:\mathrm{0}<{t}\leqslant\mathrm{1} \\ $$$${find}\:{a}\:{simple}\:{form}\:{of}\:{f}\left({t}\right)\: \\ $$$$\left.\mathrm{2}\right){calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{ln}\left(\mathrm{2}−{x}^{\mathrm{3}} \right){dx}\:. \\ $$
Commented by maxmathsup by imad last updated on 03/Aug/18
![we have f^′ (t) =−∫_0 ^1 (x^3 /(1−tx^3 ))dx =−∫_0 ^1 x^3 (Σ_(n=0) ^∞ t^n x^(3n) dx =−Σ_(n=0) ^∞ t^n ∫_0 ^1 x^(3(n+1)) dx =−Σ_(n=0) ^∞ (t^n /(3n+4)) =−(1/((^3 (√t))^4 ))Σ_(n=0) ^∞ (((^3 (√t))^(3n +4) )/(3n+4)) =−(1/((^3 (√t))^4 )) ϕ(^3 (√t)) with ϕ(x) =Σ_(n=0) ^∞ (x^(3n+4) /(3n+4)) ⇒ϕ^′ (x)= Σ_(n=0) ^∞ x^(3n+3) =x^3 Σ_(n=0) ^∞ (x^3 )^n =x^3 (1/(1−x^3 )) =(x^3 /(1−x^3 )) ⇒ϕ(x) = ∫_0 ^x (t^3 /(1−t^3 )) dt +c withc=ϕ(0)=0 ⇒ ϕ(x)=−∫_0 ^x (t^3 /(t^3 −1))dt =−∫_0 ^x ((t^3 −1 +1)/(t^3 −1))dt =−x −∫_0 ^x (dt/(t^3 −1)) let decompose F(t) = (1/(t^3 −1)) F(t)= (1/((t−1)(t^2 +t+1))) =(a/(t−1)) +((bt+c)/(t^2 +t +1)) a =lim_(t→1) (t−1)F(t) =(1/3) lim_(t→+∞) tF(t) =0 =a +b ⇒b =−a ⇒ F(t) = (1/(3(t−1))) −(1/3) ((t −3c)/(t^2 +t+1)) F(0) =−1 =−(1/3) +c ⇒c=(1/3)−1 =−(2/3) ⇒F(t)=(1/(3(t−1))) −(1/3) ((t +2)/(t^2 +t+1)) ⇒ ∫ F(t)dt = (1/3)ln∣t−1∣ −(1/6) ∫ ((2t +1+3)/(t^2 +t +1))dt =(1/3)ln∣t−1∣ −(1/6)ln∣t^2 +t+1∣ −(1/2) ∫ (dt/((t+(1/2))^2 +(3/4))) but ∫ (dt/((t+(1/2))^2 +(3/4))) =_(t+(1/2)=((√3)/2)u) ∫ (1/((3/4)(1+u^2 ))) ((√3)/2) du=(4/3) ((√3)/2) arctan(((2t+1)/( (√3)))) =((2(√3))/3) arctan(((2t+1)/( (√3)))) ⇒ ϕ(x)=−x − [ (1/3)ln∣t−1∣−(1/6)ln(t^2 +t+1)−((√3)/3) arctan(((2t+1)/( (√3))))]_0 ^x =−x −{(1/3)ln∣x−1∣−(1/6)ln(x^2 +x+1)−((√3)/3) arctan(((2x+1)/( (√3))))+((√3)/3) arctan((1/( (√3))))} we have f^′ (t)=−(1/((^3 (√t))^4 )) ϕ(^3 (√t)) so the value of f^′ (x) is known.. be continued...](https://www.tinkutara.com/question/Q41221.png)
$${we}\:{have}\:{f}^{'} \left({t}\right)\:=−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{{x}^{\mathrm{3}} }{\mathrm{1}−{tx}^{\mathrm{3}} }{dx}\:=−\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{3}} \left(\sum_{{n}=\mathrm{0}} ^{\infty} \:{t}^{{n}} \:{x}^{\mathrm{3}{n}} {dx}\right. \\ $$$$=−\sum_{{n}=\mathrm{0}} ^{\infty} \:{t}^{{n}} \:\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{\mathrm{3}\left({n}+\mathrm{1}\right)} {dx}\:=−\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{{t}^{{n}} }{\mathrm{3}{n}+\mathrm{4}} \\ $$$$=−\frac{\mathrm{1}}{\left(^{\mathrm{3}} \sqrt{{t}}\right)^{\mathrm{4}} }\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\:\frac{\left(^{\mathrm{3}} \sqrt{{t}}\right)^{\mathrm{3}{n}\:\:+\mathrm{4}} }{\mathrm{3}{n}+\mathrm{4}}\:\:=−\frac{\mathrm{1}}{\left(^{\mathrm{3}} \sqrt{{t}}\right)^{\mathrm{4}} }\:\varphi\left(^{\mathrm{3}} \sqrt{{t}}\right)\:{with}\: \\ $$$$\varphi\left({x}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\frac{{x}^{\mathrm{3}{n}+\mathrm{4}} }{\mathrm{3}{n}+\mathrm{4}}\:\Rightarrow\varphi^{'} \left({x}\right)=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:{x}^{\mathrm{3}{n}+\mathrm{3}} ={x}^{\mathrm{3}} \:\sum_{{n}=\mathrm{0}} ^{\infty} \:\left({x}^{\mathrm{3}} \right)^{{n}} \\ $$$$={x}^{\mathrm{3}} \:\frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{3}} }\:=\frac{{x}^{\mathrm{3}} }{\mathrm{1}−{x}^{\mathrm{3}} }\:\Rightarrow\varphi\left({x}\right)\:=\:\int_{\mathrm{0}} ^{{x}} \:\:\frac{{t}^{\mathrm{3}} }{\mathrm{1}−{t}^{\mathrm{3}} }\:{dt}\:+{c}\:\:{withc}=\varphi\left(\mathrm{0}\right)=\mathrm{0}\:\Rightarrow \\ $$$$\varphi\left({x}\right)=−\int_{\mathrm{0}} ^{{x}} \:\frac{{t}^{\mathrm{3}} }{{t}^{\mathrm{3}} −\mathrm{1}}{dt}\:\:\:=−\int_{\mathrm{0}} ^{{x}} \:\:\:\frac{{t}^{\mathrm{3}} −\mathrm{1}\:+\mathrm{1}}{{t}^{\mathrm{3}} −\mathrm{1}}{dt}\:=−{x}\:−\int_{\mathrm{0}} ^{{x}} \:\:\frac{{dt}}{{t}^{\mathrm{3}} \:−\mathrm{1}}\:{let}\:{decompose} \\ $$$${F}\left({t}\right)\:=\:\frac{\mathrm{1}}{{t}^{\mathrm{3}} −\mathrm{1}} \\ $$$${F}\left({t}\right)=\:\frac{\mathrm{1}}{\left({t}−\mathrm{1}\right)\left({t}^{\mathrm{2}} \:+{t}+\mathrm{1}\right)}\:=\frac{{a}}{{t}−\mathrm{1}}\:+\frac{{bt}+{c}}{{t}^{\mathrm{2}} \:+{t}\:+\mathrm{1}} \\ $$$${a}\:={lim}_{{t}\rightarrow\mathrm{1}} \left({t}−\mathrm{1}\right){F}\left({t}\right)\:=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${lim}_{{t}\rightarrow+\infty} {tF}\left({t}\right)\:=\mathrm{0}\:={a}\:+{b}\:\Rightarrow{b}\:=−{a}\:\Rightarrow \\ $$$${F}\left({t}\right)\:=\:\frac{\mathrm{1}}{\mathrm{3}\left({t}−\mathrm{1}\right)}\:−\frac{\mathrm{1}}{\mathrm{3}}\:\frac{{t}\:−\mathrm{3}{c}}{{t}^{\mathrm{2}} \:+{t}+\mathrm{1}} \\ $$$${F}\left(\mathrm{0}\right)\:=−\mathrm{1}\:=−\frac{\mathrm{1}}{\mathrm{3}}\:+{c}\:\Rightarrow{c}=\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{1}\:=−\frac{\mathrm{2}}{\mathrm{3}}\:\Rightarrow{F}\left({t}\right)=\frac{\mathrm{1}}{\mathrm{3}\left({t}−\mathrm{1}\right)}\:−\frac{\mathrm{1}}{\mathrm{3}}\:\frac{{t}\:+\mathrm{2}}{{t}^{\mathrm{2}} \:+{t}+\mathrm{1}}\:\Rightarrow \\ $$$$\int\:{F}\left({t}\right){dt}\:=\:\frac{\mathrm{1}}{\mathrm{3}}{ln}\mid{t}−\mathrm{1}\mid\:−\frac{\mathrm{1}}{\mathrm{6}}\:\int\:\frac{\mathrm{2}{t}\:+\mathrm{1}+\mathrm{3}}{{t}^{\mathrm{2}} \:+{t}\:+\mathrm{1}}{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}{ln}\mid{t}−\mathrm{1}\mid\:−\frac{\mathrm{1}}{\mathrm{6}}{ln}\mid{t}^{\mathrm{2}} \:+{t}+\mathrm{1}\mid\:−\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\:\:\frac{{dt}}{\left({t}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{4}}}\:{but} \\ $$$$\int\:\:\:\frac{{dt}}{\left({t}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{4}}}\:=_{{t}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{u}} \:\:\:\:\int\:\:\:\:\:\:\frac{\mathrm{1}}{\frac{\mathrm{3}}{\mathrm{4}}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:{du}=\frac{\mathrm{4}}{\mathrm{3}}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\:{arctan}\left(\frac{\mathrm{2}{t}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right) \\ $$$$=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\:{arctan}\left(\frac{\mathrm{2}{t}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\:\Rightarrow \\ $$$$\varphi\left({x}\right)=−{x}\:\:−\:\left[\:\frac{\mathrm{1}}{\mathrm{3}}{ln}\mid{t}−\mathrm{1}\mid−\frac{\mathrm{1}}{\mathrm{6}}{ln}\left({t}^{\mathrm{2}} \:+{t}+\mathrm{1}\right)−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\:{arctan}\left(\frac{\mathrm{2}{t}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\right]_{\mathrm{0}} ^{{x}} \\ $$$$=−{x}\:−\left\{\frac{\mathrm{1}}{\mathrm{3}}{ln}\mid{x}−\mathrm{1}\mid−\frac{\mathrm{1}}{\mathrm{6}}{ln}\left({x}^{\mathrm{2}} \:+{x}+\mathrm{1}\right)−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\:{arctan}\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)+\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\:{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\right\} \\ $$$${we}\:{have}\:{f}^{'} \left({t}\right)=−\frac{\mathrm{1}}{\left(^{\mathrm{3}} \sqrt{{t}}\right)^{\mathrm{4}} }\:\varphi\left(^{\mathrm{3}} \sqrt{{t}}\right)\:\:\:{so}\:{the}\:{value}\:{of}\:{f}^{'} \left({x}\right)\:{is}\:{known}.. \\ $$$${be}\:{continued}… \\ $$
