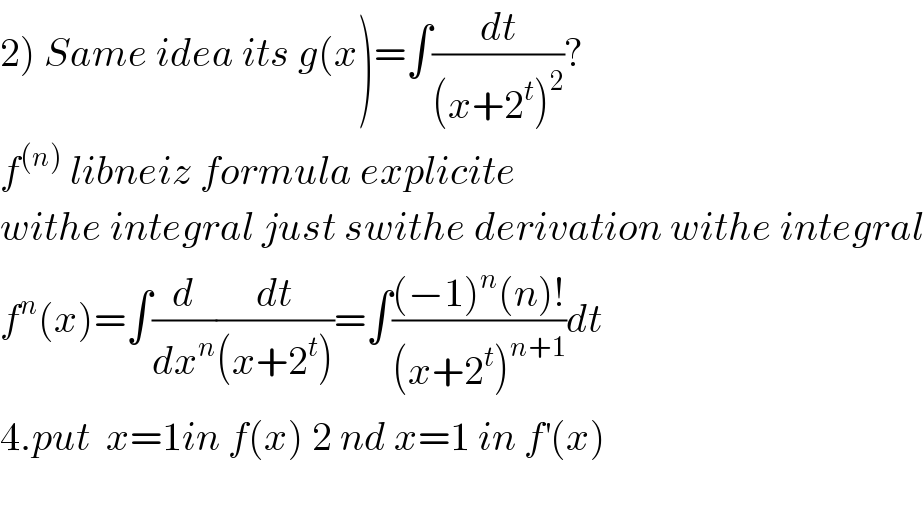Question Number 64160 by mathmax by abdo last updated on 14/Jul/19
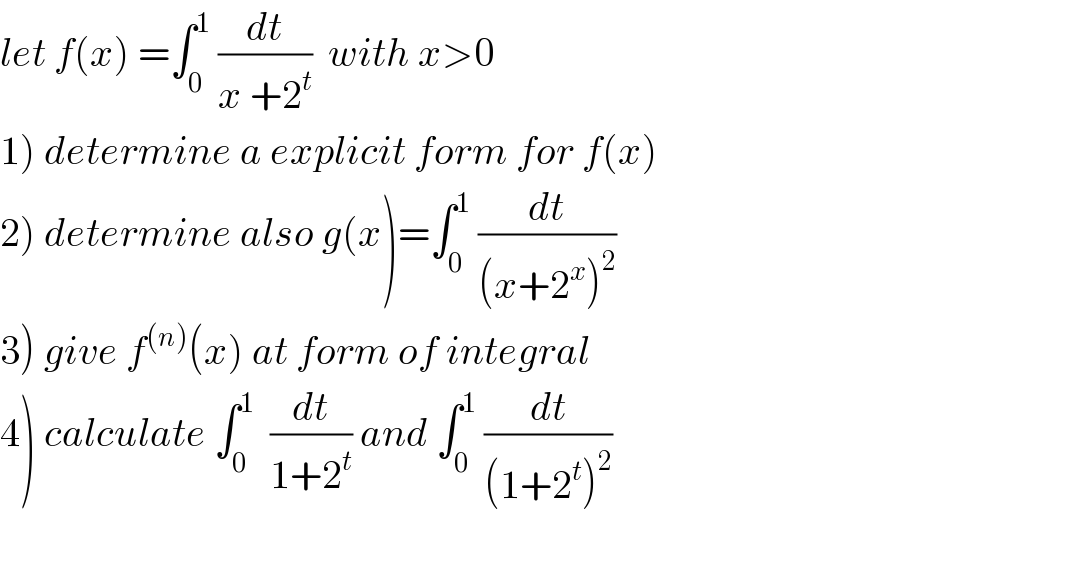
Commented by mathmax by abdo last updated on 14/Jul/19
![1)we have f(x)=∫_0 ^1 (dt/(x+2^t )) (x>0) changement 2^t =u give e^(tln2) =u ⇒tln(2)=lnu ⇒t=((ln(u))/(ln(2))) ⇒f(x) =∫_1 ^2 (du/(ln(2)u(x+u))) =(1/(ln(2))) (1/x)∫_1 ^2 {(1/u)−(1/(x+u))}du =(1/(xln(2)))[ln((u/(x+u)))]_1 ^2 =(1/(xln(2))){ln((2/(x+2)))−ln((1/(x+1)))}=(1/(xln(2))){ln2−ln(x+2)+ln(x+1)} f(x)=(1/x) +((ln(((x+1)/(x+2))))/(xln(2)))](https://www.tinkutara.com/question/Q64167.png)
Commented by mathmax by abdo last updated on 14/Jul/19
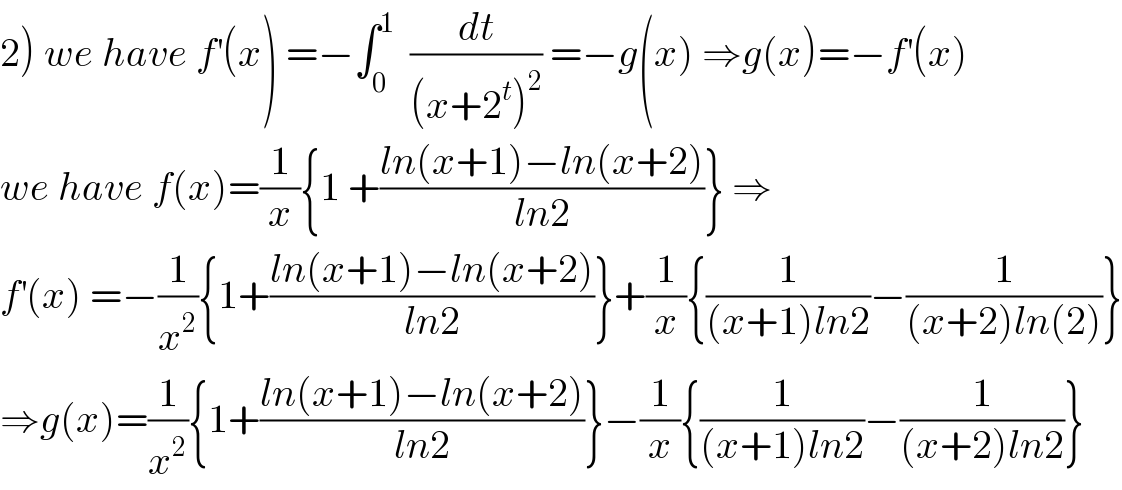
Commented by mathmax by abdo last updated on 14/Jul/19
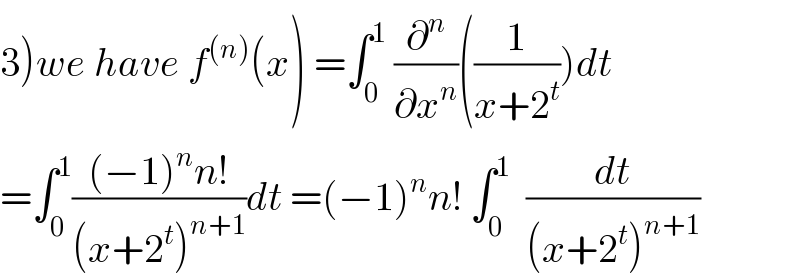
Commented by mathmax by abdo last updated on 14/Jul/19
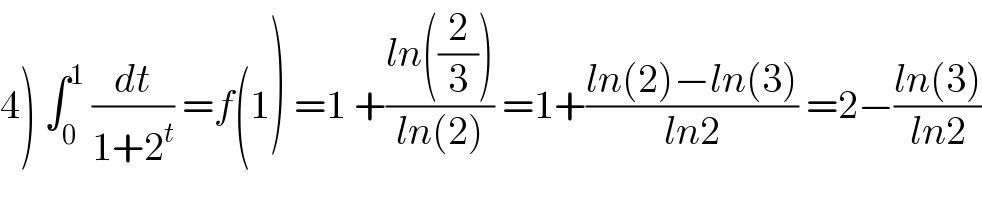
Commented by mathmax by abdo last updated on 14/Jul/19
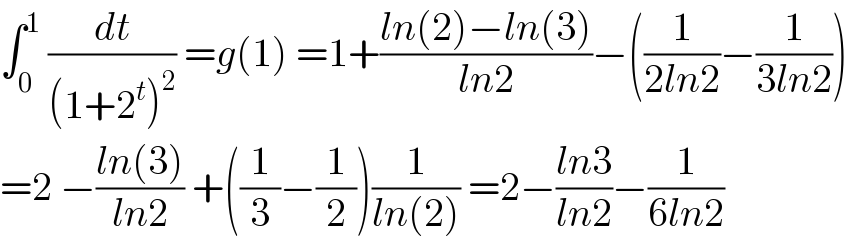
Answered by Eminem last updated on 14/Jul/19
![1) let u=2^t dt=(du/(uln(2))) f(x)=∫_1 ^2 (du/(uln(2)(x+u)))=∫_1 ^2 (du/(xuln(2)))−∫_1 ^2 (du/(xln(2)(x+u)))=(1/x)−(1/(xln(2)))[ln(x+2)−ln(x+1)]](https://www.tinkutara.com/question/Q64161.png)
Answered by Eminem last updated on 14/Jul/19