Question Number 41679 by math khazana by abdo last updated on 11/Aug/18
$${let}\:{f}\left({x}\right)\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{t}\:+{xt}^{\mathrm{2}} \right){dt} \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:{f}^{'} \left({x}\right)\:{then}\:{find}\:{a}\:{simple}\:{form}\:{of}\:{f}\left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{t}\:+{t}^{\mathrm{2}} \right){dt} \\ $$$$\left.\mathrm{3}\right)\:{calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{ln}\left(\mathrm{1}−{t}^{\mathrm{3}} \right){dt}\:. \\ $$
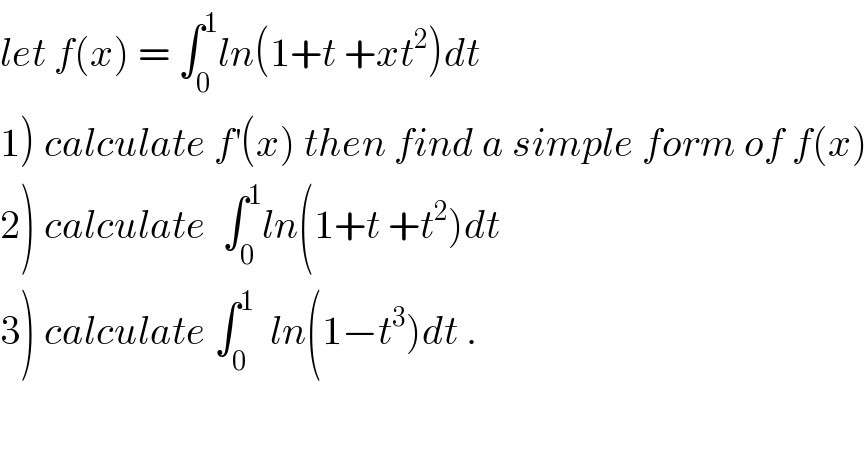
Commented by maxmathsup by imad last updated on 11/Aug/18
![1) we have f^′ (x) = ∫_0 ^1 (t^2 /(xt^2 +t+1))dt =(1/x) ∫_0 ^1 ((xt^2 +t+1−t−1)/(xt^2 +t+1))dt =(1/x) −(1/x) ∫_0 ^1 ((t+1)/(xt^2 +t +1))dt let decompose F(t) =((t+1)/(xt^2 +t +1)) Δ =1−4x case 1 1−4x>0 ⇔ x<(1/4) ⇒t_1 =((−1+(√(1−4x)))/(2x)) and t_2 =((−1−(√(1−4x)))/(2x)) F(t)=((t+1)/(x(t−t_1 )(t−t_2 ))) = (a/(t−t_1 )) +(b/(t−t_2 )) a=((t_1 +1)/(x ((2(√(1−4x)))/(2x)))) = ((t_1 +1)/( (√(1−4x)))) b = ((t_2 +1)/(x(−((2(√(1−4x)))/(2x))))) =−((t_2 +1)/( (√(1−4x)))) ⇒ ∫_0 ^1 F(t)dt = ∫_0 ^1 {(a/(t−t_1 )) +(b/(t−t_2 ))}dt =[ aln∣t−t_1 ∣ +b ln∣t−t_2 ∣]_0 ^1 = aln∣1−t_1 ∣+bln∣1−t_2 ∣−aln∣t_1 ∣−bln∣t_2 ∣ =aln∣((1−t_1 )/t_1 )∣ +bln∣((1−t_2 )/t_2 )∣ ⇒ f^′ (x)=(1/x) −(1/x){aln∣((1−t_1 )/t_1 )∣+bln∣((1−t_2 )/t_2 )∣} ⇒ f(x)=(1−λ_0 )ln∣x∣ +c with λ_0 =aln∣((1−t_1 )/t_1 )∣+bln∣((1−t_2 )/t_2 )∣(known) c=f(1) ⇒ f(x)=(1−λ_0 )ln∣x∣ +f(1)](https://www.tinkutara.com/question/Q41692.png)
$$\left.\mathrm{1}\right)\:{we}\:{have}\:{f}^{'} \left({x}\right)\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{t}^{\mathrm{2}} }{{xt}^{\mathrm{2}} \:+{t}+\mathrm{1}}{dt}\:=\frac{\mathrm{1}}{{x}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{xt}^{\mathrm{2}} \:+{t}+\mathrm{1}−{t}−\mathrm{1}}{{xt}^{\mathrm{2}} \:+{t}+\mathrm{1}}{dt} \\ $$$$=\frac{\mathrm{1}}{{x}}\:−\frac{\mathrm{1}}{{x}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{t}+\mathrm{1}}{{xt}^{\mathrm{2}} \:+{t}\:+\mathrm{1}}{dt}\:{let}\:{decompose}\:{F}\left({t}\right)\:=\frac{{t}+\mathrm{1}}{{xt}^{\mathrm{2}} \:+{t}\:+\mathrm{1}} \\ $$$$\Delta\:=\mathrm{1}−\mathrm{4}{x} \\ $$$${case}\:\mathrm{1}\:\:\mathrm{1}−\mathrm{4}{x}>\mathrm{0}\:\:\Leftrightarrow\:\:\:{x}<\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow{t}_{\mathrm{1}} =\frac{−\mathrm{1}+\sqrt{\mathrm{1}−\mathrm{4}{x}}}{\mathrm{2}{x}}\:\:{and}\:{t}_{\mathrm{2}} =\frac{−\mathrm{1}−\sqrt{\mathrm{1}−\mathrm{4}{x}}}{\mathrm{2}{x}} \\ $$$${F}\left({t}\right)=\frac{{t}+\mathrm{1}}{{x}\left({t}−{t}_{\mathrm{1}} \right)\left({t}−{t}_{\mathrm{2}} \right)}\:=\:\frac{{a}}{{t}−{t}_{\mathrm{1}} }\:+\frac{{b}}{{t}−{t}_{\mathrm{2}} } \\ $$$${a}=\frac{{t}_{\mathrm{1}} \:+\mathrm{1}}{{x}\:\frac{\mathrm{2}\sqrt{\mathrm{1}−\mathrm{4}{x}}}{\mathrm{2}{x}}}\:=\:\frac{{t}_{\mathrm{1}} +\mathrm{1}}{\:\sqrt{\mathrm{1}−\mathrm{4}{x}}} \\ $$$${b}\:=\:\frac{{t}_{\mathrm{2}} \:+\mathrm{1}}{{x}\left(−\frac{\mathrm{2}\sqrt{\mathrm{1}−\mathrm{4}{x}}}{\mathrm{2}{x}}\right)}\:=−\frac{{t}_{\mathrm{2}} +\mathrm{1}}{\:\sqrt{\mathrm{1}−\mathrm{4}{x}}}\:\:\Rightarrow\:\int_{\mathrm{0}} ^{\mathrm{1}} {F}\left({t}\right){dt}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \left\{\frac{{a}}{{t}−{t}_{\mathrm{1}} }\:+\frac{{b}}{{t}−{t}_{\mathrm{2}} }\right\}{dt} \\ $$$$=\left[\:{aln}\mid{t}−{t}_{\mathrm{1}} \mid\:+{b}\:{ln}\mid{t}−{t}_{\mathrm{2}} \mid\right]_{\mathrm{0}} ^{\mathrm{1}} \:=\:{aln}\mid\mathrm{1}−{t}_{\mathrm{1}} \mid+{bln}\mid\mathrm{1}−{t}_{\mathrm{2}} \mid−{aln}\mid{t}_{\mathrm{1}} \mid−{bln}\mid{t}_{\mathrm{2}} \mid \\ $$$$={aln}\mid\frac{\mathrm{1}−{t}_{\mathrm{1}} }{{t}_{\mathrm{1}} }\mid\:+{bln}\mid\frac{\mathrm{1}−{t}_{\mathrm{2}} }{{t}_{\mathrm{2}} }\mid\:\Rightarrow \\ $$$${f}^{'} \left({x}\right)=\frac{\mathrm{1}}{{x}}\:−\frac{\mathrm{1}}{{x}}\left\{{aln}\mid\frac{\mathrm{1}−{t}_{\mathrm{1}} }{{t}_{\mathrm{1}} }\mid+{bln}\mid\frac{\mathrm{1}−{t}_{\mathrm{2}} }{{t}_{\mathrm{2}} }\mid\right\}\:\Rightarrow \\ $$$${f}\left({x}\right)=\left(\mathrm{1}−\lambda_{\mathrm{0}} \right){ln}\mid{x}\mid\:+{c}\:\:\:{with}\:\:\:\lambda_{\mathrm{0}} \:={aln}\mid\frac{\mathrm{1}−{t}_{\mathrm{1}} }{{t}_{\mathrm{1}} }\mid+{bln}\mid\frac{\mathrm{1}−{t}_{\mathrm{2}} }{{t}_{\mathrm{2}} }\mid\left({known}\right) \\ $$$${c}={f}\left(\mathrm{1}\right)\:\Rightarrow\:{f}\left({x}\right)=\left(\mathrm{1}−\lambda_{\mathrm{0}} \right){ln}\mid{x}\mid\:+{f}\left(\mathrm{1}\right) \\ $$
Commented by maxmathsup by imad last updated on 11/Aug/18
![case 2 1−4x<0 ⇒no real roots if x>(1/4) ∫_0 ^1 F(x)dx = ∫_0 ^1 ((t+1)/(xt^2 +t +1)) dt =(1/(2x)) ∫_0 ^1 ((2xt +1 +2x −1)/(xt^2 +t +1)) dt =(1/(2x))[ln∣xt^2 +t+1∣]_0 ^1 +(1/(2x)) ∫_0 ^1 ((2x−1)/(xt^2 +t +1))dt =(1/(2x))ln∣ x+2∣ +((2x−1)/(2x^2 )) ∫_0 ^1 (dt/(t^2 +(t/x) +(1/x))) but ∫_0 ^1 (dt/(t^2 +(t/x)+(1/x))) = ∫_0 ^1 (dt/(t^2 +2(t/(2x)) + (1/(4x^2 )) +(1/x)−(1/(4x^2 )))) =∫_0 ^1 (dt/((t+(1/(2x)))^2 +((4x−1)/(4x^2 )))) =_(t+(1/(2x))= ((√(4x−1))/(2x))u) ∫_(1/( (√(4x−1)))) ^((2x+1)/( (√(4x−1)))) (1/(((4x−1)/(4x^2 ))(1+u^2 ))) ((√(4x−1))/(2x)) du =((4x^2 )/(4x−1)) .((√(4x−1))/(2x)) { arctan(((2x+1)/( (√(4x−1)))))−arctan((1/( (√(4x−1)))))} = ((2x)/( (√(4x−1)))) { arctan(((2x+1)/( (√(4x−1)))))−arctan((1/( (√(4x−1)))))}⇒ f^′ (x) = (1/x) −(2/( (√(4x−1)))){ arctan(((2x+1)/( (√(4x−1)))))−arctan((1/( (√(4x−1)))))} ⇒](https://www.tinkutara.com/question/Q41693.png)
$${case}\:\mathrm{2}\:\:\mathrm{1}−\mathrm{4}{x}<\mathrm{0}\:\Rightarrow{no}\:{real}\:{roots}\:{if}\:{x}>\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:{F}\left({x}\right){dx}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{{t}+\mathrm{1}}{{xt}^{\mathrm{2}} \:+{t}\:+\mathrm{1}}\:{dt}\:=\frac{\mathrm{1}}{\mathrm{2}{x}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{2}{xt}\:+\mathrm{1}\:+\mathrm{2}{x}\:−\mathrm{1}}{{xt}^{\mathrm{2}} \:+{t}\:+\mathrm{1}}\:{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{x}}\left[{ln}\mid{xt}^{\mathrm{2}} +{t}+\mathrm{1}\mid\right]_{\mathrm{0}} ^{\mathrm{1}} \:\:+\frac{\mathrm{1}}{\mathrm{2}{x}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{\mathrm{2}{x}−\mathrm{1}}{{xt}^{\mathrm{2}} \:+{t}\:+\mathrm{1}}{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{x}}{ln}\mid\:{x}+\mathrm{2}\mid\:\:+\frac{\mathrm{2}{x}−\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\:\frac{{dt}}{{t}^{\mathrm{2}} \:+\frac{{t}}{{x}}\:+\frac{\mathrm{1}}{{x}}}\:{but} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{{dt}}{{t}^{\mathrm{2}} \:+\frac{{t}}{{x}}+\frac{\mathrm{1}}{{x}}}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{{dt}}{{t}^{\mathrm{2}} \:+\mathrm{2}\frac{{t}}{\mathrm{2}{x}}\:+\:\frac{\mathrm{1}}{\mathrm{4}{x}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{\mathrm{4}{x}^{\mathrm{2}} }}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{{dt}}{\left({t}+\frac{\mathrm{1}}{\mathrm{2}{x}}\right)^{\mathrm{2}} \:+\frac{\mathrm{4}{x}−\mathrm{1}}{\mathrm{4}{x}^{\mathrm{2}} }} \\ $$$$=_{{t}+\frac{\mathrm{1}}{\mathrm{2}{x}}=\:\frac{\sqrt{\mathrm{4}{x}−\mathrm{1}}}{\mathrm{2}{x}}{u}} \:\:\:\:\:\:\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{4}{x}−\mathrm{1}}}} ^{\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{4}{x}−\mathrm{1}}}} \:\:\:\:\:\:\:\frac{\mathrm{1}}{\frac{\mathrm{4}{x}−\mathrm{1}}{\mathrm{4}{x}^{\mathrm{2}} }\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}\:\:\frac{\sqrt{\mathrm{4}{x}−\mathrm{1}}}{\mathrm{2}{x}}\:{du} \\ $$$$=\frac{\mathrm{4}{x}^{\mathrm{2}} }{\mathrm{4}{x}−\mathrm{1}}\:.\frac{\sqrt{\mathrm{4}{x}−\mathrm{1}}}{\mathrm{2}{x}}\:\:\left\{\:\:{arctan}\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{4}{x}−\mathrm{1}}}\right)−{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{4}{x}−\mathrm{1}}}\right)\right\} \\ $$$$=\:\frac{\mathrm{2}{x}}{\:\sqrt{\mathrm{4}{x}−\mathrm{1}}}\:\left\{\:{arctan}\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{4}{x}−\mathrm{1}}}\right)−{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{4}{x}−\mathrm{1}}}\right)\right\}\Rightarrow \\ $$$${f}^{'} \left({x}\right)\:=\:\frac{\mathrm{1}}{{x}}\:−\frac{\mathrm{2}}{\:\sqrt{\mathrm{4}{x}−\mathrm{1}}}\left\{\:\:{arctan}\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{4}{x}−\mathrm{1}}}\right)−{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{4}{x}−\mathrm{1}}}\right)\right\}\:\Rightarrow \\ $$
Commented by maxmathsup by imad last updated on 11/Aug/18
$${f}\left({x}\right)={ln}\left({x}\right)\:−\int\:\:\:\:\:\frac{\mathrm{2}\left\{\:{arctan}\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{4}{x}−\mathrm{1}}}\right)−{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{4}{x}−\mathrm{1}}}\right)\right\}}{\:\sqrt{\mathrm{4}{x}−\mathrm{1}}}\:{dx}\:+{c}..{be} \\ $$$${continued}\:.. \\ $$
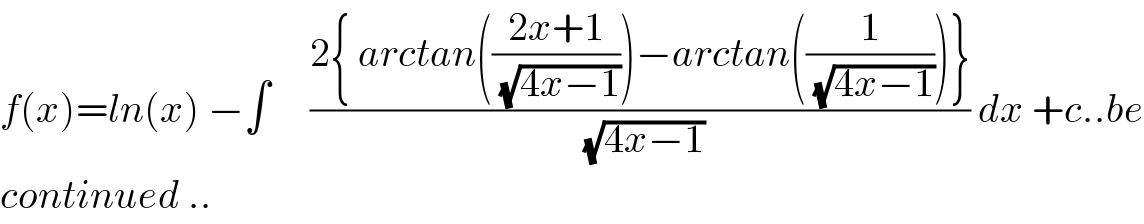
Commented by maxmathsup by imad last updated on 11/Aug/18
![2) by parts ∫_0 ^1 ln(t^2 +t+1)dt =[tln(t^2 +t+1)]_0 ^1 −∫_0 ^1 t ((2t+1)/(t^2 +t+1))dt =ln(3) −∫_0 ^1 ((2t^2 +t)/(t^2 +t +1)) dt but ∫_0 ^1 ((2t^2 +t)/(t^2 +t +1)) dt = ∫_0 ^1 ((2(t^2 +t+1) +t−2t−2)/(t^2 +t+1)) dt=2 −∫_0 ^1 ((t+2)/(t^2 +t +1))dt =2−(1/2) ∫_0 ^1 ((2t+1+3)/(t^2 +t +1)) dt =2−(1/2)[ln∣t^2 +t+1∣_0 ^1 −(3/2) ∫_0 ^1 (dt/(t^2 +t+1)) =2−(1/2)ln(3) −(3/2) ∫_0 ^1 (dt/((t+(1/2))^2 +(3/4))) =_(t+(1/2)=((√3)/2)u) 2−((ln(3))/2) −(3/2) (4/3) ∫_(1/( (√3))) ^(√3) (1/(1+u^2 )) ((√3)/2)du =2−((ln(3))/2) −(√3)[arctanu]_(1/( (√3))) ^(√3) =2−((ln(3))/2) −(√3){ (π/3) −(π/6)} =2−((ln(3))/2) −(π/6)(√3) ⇒ ∫_0 ^1 ln(1+t +t^2 )dt =ln(3) −2 +((ln(3))/2) +((π(√3))/6) =(3/2)ln(3) +((π(√3))/6) −2 .](https://www.tinkutara.com/question/Q41697.png)
$$\left.\mathrm{2}\right)\:{by}\:{parts}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left({t}^{\mathrm{2}} \:+{t}+\mathrm{1}\right){dt}\:=\left[{tln}\left({t}^{\mathrm{2}} \:+{t}+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{t}\:\frac{\mathrm{2}{t}+\mathrm{1}}{{t}^{\mathrm{2}} \:+{t}+\mathrm{1}}{dt} \\ $$$$={ln}\left(\mathrm{3}\right)\:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{\mathrm{2}{t}^{\mathrm{2}} \:+{t}}{{t}^{\mathrm{2}} \:+{t}\:+\mathrm{1}}\:{dt}\:{but} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{\mathrm{2}{t}^{\mathrm{2}} \:+{t}}{{t}^{\mathrm{2}} \:+{t}\:+\mathrm{1}}\:{dt}\:=\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{\mathrm{2}\left({t}^{\mathrm{2}} \:+{t}+\mathrm{1}\right)\:+{t}−\mathrm{2}{t}−\mathrm{2}}{{t}^{\mathrm{2}} \:+{t}+\mathrm{1}}\:{dt}=\mathrm{2}\:\:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{t}+\mathrm{2}}{{t}^{\mathrm{2}} \:+{t}\:+\mathrm{1}}{dt} \\ $$$$=\mathrm{2}−\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{\mathrm{2}{t}+\mathrm{1}+\mathrm{3}}{{t}^{\mathrm{2}} \:+{t}\:+\mathrm{1}}\:{dt}\:=\mathrm{2}−\frac{\mathrm{1}}{\mathrm{2}}\left[{ln}\mid{t}^{\mathrm{2}} \:+{t}+\mathrm{1}\mid_{\mathrm{0}} ^{\mathrm{1}} \:−\frac{\mathrm{3}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dt}}{{t}^{\mathrm{2}} \:+{t}+\mathrm{1}}\right. \\ $$$$=\mathrm{2}−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{3}\right)\:−\frac{\mathrm{3}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{dt}}{\left({t}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}}\:=_{{t}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{u}} \:\:\:\mathrm{2}−\frac{{ln}\left(\mathrm{3}\right)}{\mathrm{2}}\:−\frac{\mathrm{3}}{\mathrm{2}}\:\frac{\mathrm{4}}{\mathrm{3}}\:\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{\sqrt{\mathrm{3}}} \:\:\frac{\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{2}} }\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{du} \\ $$$$=\mathrm{2}−\frac{{ln}\left(\mathrm{3}\right)}{\mathrm{2}}\:−\sqrt{\mathrm{3}}\left[{arctanu}\right]_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{\sqrt{\mathrm{3}}} \:=\mathrm{2}−\frac{{ln}\left(\mathrm{3}\right)}{\mathrm{2}}\:−\sqrt{\mathrm{3}}\left\{\:\frac{\pi}{\mathrm{3}}\:−\frac{\pi}{\mathrm{6}}\right\} \\ $$$$=\mathrm{2}−\frac{{ln}\left(\mathrm{3}\right)}{\mathrm{2}}\:−\frac{\pi}{\mathrm{6}}\sqrt{\mathrm{3}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{t}\:+{t}^{\mathrm{2}} \right){dt}\:={ln}\left(\mathrm{3}\right)\:−\mathrm{2}\:+\frac{{ln}\left(\mathrm{3}\right)}{\mathrm{2}}\:+\frac{\pi\sqrt{\mathrm{3}}}{\mathrm{6}}\:=\frac{\mathrm{3}}{\mathrm{2}}{ln}\left(\mathrm{3}\right)\:+\frac{\pi\sqrt{\mathrm{3}}}{\mathrm{6}}\:−\mathrm{2}\:. \\ $$
Commented by maxmathsup by imad last updated on 11/Aug/18
![3) ∫_0 ^1 ln(1−t^3 )dt =∫_0 ^1 ln(1−t) dt +∫_0 ^1 ln(1+t+t^2 )dtbut ∫_0 ^1 ln(1−t)dt =_(1−t=x) ∫_0 ^1 ln(x)dx =[xln(x)−x]_0 ^1 =−1 ⇒ ∫_0 ^1 ln(1−x^3 )dx =−1 +(3/2)ln(3)+((π(√3))/6) −2 =−3 +(3/2)ln(3) +((π(√3))/6) .](https://www.tinkutara.com/question/Q41698.png)
$$\left.\mathrm{3}\right)\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}−{t}^{\mathrm{3}} \right){dt}\:=\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}−{t}\right)\:{dt}\:+\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{t}+{t}^{\mathrm{2}} \right){dtbut} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:{ln}\left(\mathrm{1}−{t}\right){dt}\:=_{\mathrm{1}−{t}={x}} \:\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left({x}\right){dx}\:=\left[{xln}\left({x}\right)−{x}\right]_{\mathrm{0}} ^{\mathrm{1}} =−\mathrm{1}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}−{x}^{\mathrm{3}} \right){dx}\:=−\mathrm{1}\:+\frac{\mathrm{3}}{\mathrm{2}}{ln}\left(\mathrm{3}\right)+\frac{\pi\sqrt{\mathrm{3}}}{\mathrm{6}}\:−\mathrm{2}\: \\ $$$$=−\mathrm{3}\:+\frac{\mathrm{3}}{\mathrm{2}}{ln}\left(\mathrm{3}\right)\:+\frac{\pi\sqrt{\mathrm{3}}}{\mathrm{6}}\:. \\ $$
Answered by alex041103 last updated on 11/Aug/18
![1+t+xt^2 =x(t−t_1 )(t−t_2 ) t_(1,2) =((−1±(√(1−4x)))/(2x)) ⇒f(x)=∫_0 ^1 ln(x)dt+∫_0 ^1 ln(t−t_1 )dt +∫_0 ^1 ln(t−t_2 )dt As we know ∫ln(x)dx=x(ln(x)−1) ⇒f(x)=ln(x)+ln(1−t_1 ) +ln(1−t_2 )−2= =ln(x(1−t_1 )(1−t_2 ))−2= =ln(2+x)−2 ⇒f(x)=ln(2+x)−2 ⇒∫_0 ^1 ln(1+t +t^2 )dt=f(x=1)=ln(3)−2 ⇒∫_0 ^1 ln(1−t^3 )dt 1−t^3 =(1−t)(1+t+t^2 ) ⇒∫_0 ^1 ln(1−t^3 )dt=∫_0 ^1 ln(1−t)dt+f(1)= =[(1−t)(ln(1−t)−1)]_1 ^0 +f(1)= =[−1−lim_(t→1^− ) ((ln(1−t)−1)/(1/(1−t)))]+f(1)= =−[1+lim_(t→1^− ) ((−(1/(1−t)))/(1/((1−t)^2 )))]+f(1)= =−1+ln(3)−2 ⇒∫_0 ^1 ln(1−t^3 )dt=ln(3)−3](https://www.tinkutara.com/question/Q41680.png)
$$\mathrm{1}+{t}+{xt}^{\mathrm{2}} ={x}\left({t}−{t}_{\mathrm{1}} \right)\left({t}−{t}_{\mathrm{2}} \right) \\ $$$${t}_{\mathrm{1},\mathrm{2}} =\frac{−\mathrm{1}\pm\sqrt{\mathrm{1}−\mathrm{4}{x}}}{\mathrm{2}{x}} \\ $$$$\Rightarrow{f}\left({x}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left({x}\right){dt}+\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left({t}−{t}_{\mathrm{1}} \right){dt}\:+\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left({t}−{t}_{\mathrm{2}} \right){dt} \\ $$$${As}\:{we}\:{know}\:\int{ln}\left({x}\right){dx}={x}\left({ln}\left({x}\right)−\mathrm{1}\right) \\ $$$$\Rightarrow{f}\left({x}\right)={ln}\left({x}\right)+{ln}\left(\mathrm{1}−{t}_{\mathrm{1}} \right)\:+{ln}\left(\mathrm{1}−{t}_{\mathrm{2}} \right)−\mathrm{2}= \\ $$$$={ln}\left({x}\left(\mathrm{1}−{t}_{\mathrm{1}} \right)\left(\mathrm{1}−{t}_{\mathrm{2}} \right)\right)−\mathrm{2}= \\ $$$$={ln}\left(\mathrm{2}+{x}\right)−\mathrm{2} \\ $$$$\Rightarrow{f}\left({x}\right)={ln}\left(\mathrm{2}+{x}\right)−\mathrm{2} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{t}\:+{t}^{\mathrm{2}} \right){dt}={f}\left({x}=\mathrm{1}\right)={ln}\left(\mathrm{3}\right)−\mathrm{2} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}−{t}^{\mathrm{3}} \right){dt} \\ $$$$\mathrm{1}−{t}^{\mathrm{3}} =\left(\mathrm{1}−{t}\right)\left(\mathrm{1}+{t}+{t}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}−{t}^{\mathrm{3}} \right){dt}=\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}−{t}\right){dt}+{f}\left(\mathrm{1}\right)= \\ $$$$=\left[\left(\mathrm{1}−{t}\right)\left({ln}\left(\mathrm{1}−{t}\right)−\mathrm{1}\right)\right]_{\mathrm{1}} ^{\mathrm{0}} +{f}\left(\mathrm{1}\right)= \\ $$$$=\left[−\mathrm{1}−\underset{{t}\rightarrow\mathrm{1}^{−} } {{lim}}\frac{{ln}\left(\mathrm{1}−{t}\right)−\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{1}−{t}}}\right]+{f}\left(\mathrm{1}\right)= \\ $$$$=−\left[\mathrm{1}+\underset{{t}\rightarrow\mathrm{1}^{−} } {{lim}}\frac{−\frac{\mathrm{1}}{\mathrm{1}−{t}}}{\frac{\mathrm{1}}{\left(\mathrm{1}−{t}\right)^{\mathrm{2}} }}\right]+{f}\left(\mathrm{1}\right)= \\ $$$$=−\mathrm{1}+{ln}\left(\mathrm{3}\right)−\mathrm{2} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}−{t}^{\mathrm{3}} \right){dt}={ln}\left(\mathrm{3}\right)−\mathrm{3} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$