Menu Close

let-f-x-0-1-ln-1-xt-2-1-t-2-dt-1-find-a-simple-form-of-f-x-2-calculate-0-1-ln-1-t-2-1-t-2-dt-3-calculate-0-1-ln-1-2t-2-1-t-2-dt-

Tinku Tara 0 Comments
Pin




Question Number 41762 by math khazana by abdo last updated on 12/Aug/18
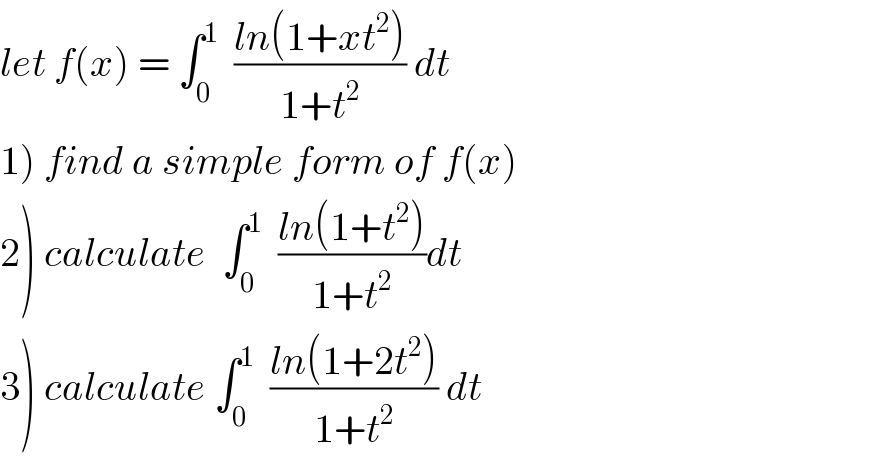
let f(x) = ∫_0 ^1 ((ln(1+xt^2 ))/(1+t^2 )) dt 1) find a simple form of f(x) 2) calculate ∫_0 ^1 ((ln(1+t^2 ))/(1+t^2 ))dt 3) calculate ∫_0 ^1 ((ln(1+2t^2 ))/(1+t^2 )) dt
$${let}\:{f}\left({x}\right)\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{ln}\left(\mathrm{1}+{xt}^{\mathrm{2}} \right)}{\mathrm{1}+{t}^{\mathrm{2}} }\:{dt} \\ $$$$\left.\mathrm{1}\right)\:{find}\:{a}\:{simple}\:{form}\:{of}\:{f}\left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$$\left.\mathrm{3}\right)\:{calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{ln}\left(\mathrm{1}+\mathrm{2}{t}^{\mathrm{2}} \right)}{\mathrm{1}+{t}^{\mathrm{2}} }\:{dt} \\ $$
Commented by math khazana by abdo last updated on 13/Aug/18
we have f^′ (x)= ∫_0 ^1 (t^2 /((1+xt^2 )(1+t^2 )))dt let decompose F(t) =(t^2 /((1+xt^2 )(1+t^2 ))) F(t)= ((at+b)/(t^2 +1)) +((ct +d)/(xt^2 +1)) F(−t)=F(t) ⇒((−at +b)/(t^2 +1)) +((−ct +d)/(xt^2 +1)) =F(t) ⇒ a=c=0⇒F(t)=(b/(t^2 +1)) +(d/(xt^2 +1)) lim_(t→+∞) t^2 F(t)=(1/x) =b +(d/x) ⇒1=bx +d ⇒ d=1−bx ⇒F(t)=(b/(t^2 +1)) +((1−bx)/(xt^2 +1)) F(0) =0 =b +1−bx =(1−x)b +1 ⇒b=(1/(x−1)) d=1−(x/(x−1)) =((−1)/(x−1)) ⇒ F(t)= (1/((x−1)(t^2 +1))) −(1/((x−1)(xt^2 +1))) ⇒ f^′ (x) =(1/(x−1)) ∫_0 ^1 (dt/(1+t^2 )) −(1/(x−1)) ∫_0 ^1 (dx/(1+xt^2 )) =(π/(4(x−1))) −(1/(x−1)) ∫_0 ^1 (dt/(1+xt^2 )) case1 x>0 changement t(√x)=u give ∫_0 ^1 (dt/(1+xt^2 )) = ∫_0 ^(√x) (1/(1+u^2 )) (du/( (√x))) =(1/( (√x))) arctan((√x))⇒ f^′ (x) =(π/(4(x−1))) −((arctan((√x)))/((x−1)(√x))) ⇒ f(x) =(π/4) ∫_0 ^x (dt/(t−1)) − ∫_0 ^x ((arctan((√t)))/((t−1)(√t))) +c c=f(0)=0 ⇒f(x)=(π/4)ln∣x−1∣ −∫_0 ^x ((arctan((√t)))/((t−1)(√t)))dt but ∫_0 ^x ((arctan((√t)))/((t−1)(√t))) dt =_((√t)=u) 2∫_0 ^(√x) ((arctan(u))/((u^2 −1)u)) udu =2 ∫_0 ^(√x) ((arctan(u))/(u^2 −1)) du ⇒ f(x)=(π/4)ln∣x−1∣ +2 ∫_0 ^(√x) ((arctanu)/(1−u^2 )) du
$${we}\:{have}\:{f}^{'} \left({x}\right)=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{t}^{\mathrm{2}} }{\left(\mathrm{1}+{xt}^{\mathrm{2}} \right)\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{dt} \\ $$$${let}\:{decompose}\:{F}\left({t}\right)\:=\frac{{t}^{\mathrm{2}} }{\left(\mathrm{1}+{xt}^{\mathrm{2}} \right)\left(\mathrm{1}+{t}^{\mathrm{2}} \right)} \\ $$$${F}\left({t}\right)=\:\frac{{at}+{b}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{{ct}\:+{d}}{{xt}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${F}\left(−{t}\right)={F}\left({t}\right)\:\Rightarrow\frac{−{at}\:+{b}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{−{ct}\:+{d}}{{xt}^{\mathrm{2}} \:+\mathrm{1}}\:={F}\left({t}\right)\:\Rightarrow \\ $$$${a}={c}=\mathrm{0}\Rightarrow{F}\left({t}\right)=\frac{{b}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{{d}}{{xt}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${lim}_{{t}\rightarrow+\infty} {t}^{\mathrm{2}} \:{F}\left({t}\right)=\frac{\mathrm{1}}{{x}}\:={b}\:\:+\frac{{d}}{{x}}\:\Rightarrow\mathrm{1}={bx}\:+{d}\:\Rightarrow \\ $$$${d}=\mathrm{1}−{bx}\:\Rightarrow{F}\left({t}\right)=\frac{{b}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{\mathrm{1}−{bx}}{{xt}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${F}\left(\mathrm{0}\right)\:=\mathrm{0}\:={b}\:+\mathrm{1}−{bx}\:=\left(\mathrm{1}−{x}\right){b}\:+\mathrm{1}\:\Rightarrow{b}=\frac{\mathrm{1}}{{x}−\mathrm{1}} \\ $$$${d}=\mathrm{1}−\frac{{x}}{{x}−\mathrm{1}}\:=\frac{−\mathrm{1}}{{x}−\mathrm{1}}\:\Rightarrow \\ $$$${F}\left({t}\right)=\:\:\frac{\mathrm{1}}{\left({x}−\mathrm{1}\right)\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)}\:−\frac{\mathrm{1}}{\left({x}−\mathrm{1}\right)\left({xt}^{\mathrm{2}} \:+\mathrm{1}\right)}\:\Rightarrow \\ $$$${f}^{'} \left({x}\right)\:=\frac{\mathrm{1}}{{x}−\mathrm{1}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:−\frac{\mathrm{1}}{{x}−\mathrm{1}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{dx}}{\mathrm{1}+{xt}^{\mathrm{2}} } \\ $$$$=\frac{\pi}{\mathrm{4}\left({x}−\mathrm{1}\right)}\:−\frac{\mathrm{1}}{{x}−\mathrm{1}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{dt}}{\mathrm{1}+{xt}^{\mathrm{2}} } \\ $$$${case}\mathrm{1}\:\:{x}>\mathrm{0}\:\:{changement}\:{t}\sqrt{{x}}={u}\:{give} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{{dt}}{\mathrm{1}+{xt}^{\mathrm{2}} }\:=\:\int_{\mathrm{0}} ^{\sqrt{{x}}} \:\:\:\:\frac{\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{2}} }\:\frac{{du}}{\:\sqrt{{x}}}\:=\frac{\mathrm{1}}{\:\sqrt{{x}}}\:{arctan}\left(\sqrt{{x}}\right)\Rightarrow \\ $$$${f}^{'} \left({x}\right)\:=\frac{\pi}{\mathrm{4}\left({x}−\mathrm{1}\right)}\:−\frac{{arctan}\left(\sqrt{{x}}\right)}{\left({x}−\mathrm{1}\right)\sqrt{{x}}}\:\Rightarrow \\ $$$${f}\left({x}\right)\:=\frac{\pi}{\mathrm{4}}\:\int_{\mathrm{0}} ^{{x}} \:\:\:\frac{{dt}}{{t}−\mathrm{1}}\:\:−\:\int_{\mathrm{0}} ^{{x}} \:\:\:\:\frac{{arctan}\left(\sqrt{{t}}\right)}{\left({t}−\mathrm{1}\right)\sqrt{{t}}}\:+{c} \\ $$$${c}={f}\left(\mathrm{0}\right)=\mathrm{0}\:\Rightarrow{f}\left({x}\right)=\frac{\pi}{\mathrm{4}}{ln}\mid{x}−\mathrm{1}\mid\:−\int_{\mathrm{0}} ^{{x}} \:\:\frac{{arctan}\left(\sqrt{{t}}\right)}{\left({t}−\mathrm{1}\right)\sqrt{{t}}}{dt} \\ $$$${but}\:\:\int_{\mathrm{0}} ^{{x}} \:\:\:\frac{{arctan}\left(\sqrt{{t}}\right)}{\left({t}−\mathrm{1}\right)\sqrt{{t}}}\:{dt}\:=_{\sqrt{{t}}={u}} \:\:\mathrm{2}\int_{\mathrm{0}} ^{\sqrt{{x}}} \:\:\:\frac{{arctan}\left({u}\right)}{\left({u}^{\mathrm{2}} −\mathrm{1}\right){u}}\:{udu} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\sqrt{{x}}} \:\:\:\frac{{arctan}\left({u}\right)}{{u}^{\mathrm{2}} −\mathrm{1}}\:{du}\:\Rightarrow \\ $$$${f}\left({x}\right)=\frac{\pi}{\mathrm{4}}{ln}\mid{x}−\mathrm{1}\mid\:+\mathrm{2}\:\:\int_{\mathrm{0}} ^{\sqrt{{x}}} \:\:\:\:\frac{{arctanu}}{\mathrm{1}−{u}^{\mathrm{2}} }\:{du} \\ $$
Commented by math khazana by abdo last updated on 13/Aug/18
case 2 x<0 ∫_0 ^1 (dx/(1+xt^2 )) = ∫_0 ^1 (dt/(1−((√(−x))t)^2 )) =_((√(−x))t =u) ∫_0 ^(√(−x)) (1/(1−u^2 )) (du/( (√(−x)))) =(1/( (√(−x)))) ∫_0 ^(√(−x)) (du/(1−u^2 )) = (1/(2(√(−x)))) ∫_0 ^(√(−x)) ((1/(1−u)) +(1/(1+u)))du =(1/(2(√(−x))))[ln∣((1+u)/(1−u))∣]_0 ^(√(−x)) = (1/(2(√(−x))))ln∣((1+(√(−x)))/(1−(√(−x))))∣ ⇒ f^′ (x) = (π/(4(x−1))) −(1/(2(x−1)(√(−x))))ln∣((1+(√(−x)))/(1−(√(−x))))∣ ⇒ f(x)=(π/4)ln∣x−1∣ −∫ (1/(2(x−1)(√(−x))))ln∣((1+(√(−x)))/(1−(√(−x))))∣dx +c
$${case}\:\mathrm{2}\:\:{x}<\mathrm{0}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{{dx}}{\mathrm{1}+{xt}^{\mathrm{2}} }\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{dt}}{\mathrm{1}−\left(\sqrt{−{x}}{t}\right)^{\mathrm{2}} } \\ $$$$=_{\sqrt{−{x}}{t}\:={u}} \:\:\int_{\mathrm{0}} ^{\sqrt{−{x}}} \:\:\:\:\frac{\mathrm{1}}{\mathrm{1}−{u}^{\mathrm{2}} }\:\frac{{du}}{\:\sqrt{−{x}}} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{−{x}}}\:\int_{\mathrm{0}} ^{\sqrt{−{x}}} \:\:\frac{{du}}{\mathrm{1}−{u}^{\mathrm{2}} }\:=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{−{x}}}\:\int_{\mathrm{0}} ^{\sqrt{−{x}}} \:\:\left(\frac{\mathrm{1}}{\mathrm{1}−{u}}\:+\frac{\mathrm{1}}{\mathrm{1}+{u}}\right){du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{−{x}}}\left[{ln}\mid\frac{\mathrm{1}+{u}}{\mathrm{1}−{u}}\mid\right]_{\mathrm{0}} ^{\sqrt{−{x}}} \:=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{−{x}}}{ln}\mid\frac{\mathrm{1}+\sqrt{−{x}}}{\mathrm{1}−\sqrt{−{x}}}\mid\:\Rightarrow \\ $$$${f}^{'} \left({x}\right)\:=\:\frac{\pi}{\mathrm{4}\left({x}−\mathrm{1}\right)}\:−\frac{\mathrm{1}}{\mathrm{2}\left({x}−\mathrm{1}\right)\sqrt{−{x}}}{ln}\mid\frac{\mathrm{1}+\sqrt{−{x}}}{\mathrm{1}−\sqrt{−{x}}}\mid\:\Rightarrow \\ $$$${f}\left({x}\right)=\frac{\pi}{\mathrm{4}}{ln}\mid{x}−\mathrm{1}\mid\:−\int\:\:\frac{\mathrm{1}}{\mathrm{2}\left({x}−\mathrm{1}\right)\sqrt{−{x}}}{ln}\mid\frac{\mathrm{1}+\sqrt{−{x}}}{\mathrm{1}−\sqrt{−{x}}}\mid{dx}\:+{c} \\ $$$$ \\ $$
Commented by math khazana by abdo last updated on 13/Aug/18
2) let A = ∫_0 ^1 ((ln(1+t^2 ))/(1+t^2 ))dt A=_(t=tanθ) ∫_0 ^(π/4) ((ln(1+tan^2 θ))/(1+tan^2 θ)) (1+tan^2 θ)dθ = ∫_0 ^(π/4) ln((1/(cos^2 θ)))dθ =−2 ∫_0 ^(π/4) ln(cosθ)dθ let H = ∫_0 ^(π/4) ln(cosθ)dθ and K = ∫_0 ^(π/4) ln(sinθ)dθ we have H =_(θ=(π/2)−t) −∫_(π/2) ^(π/4) ln(sint)dt = ∫_(π/4) ^(π/2) ln(sint)dt = −∫_0 ^(π/4) ln(sint)dt +∫_0 ^(π/2) ln(sint)dt =−K −(π/2)ln(2) ⇒ H +K =−(π/2)ln(2) K−H = ∫_0 ^(π/4) ln(sinθ)dθ −∫_0 ^(π/4) ln(cosθ)dθ =∫_0 ^(π/4) ln(tanθ)dθ =_(tanθ =u) ∫_0 ^1 ((ln(u))/(1+u^2 )) du =∫_0 ^1 (Σ_(n=0) ^∞ (−1)^n u^(2n) )ln(u) du =Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 u^(2n) ln(u)du by parts A_n = ∫_0 ^1 u^(2n) ln(u)du = [(1/(2n+1))u^(2n+1) ln(u)]_0 ^1 −∫_0 ^1 (1/((2n+1))) u^(2n) du =−(1/((2n+1)^2 )) ⇒ K−H = Σ_(n=0) ^∞ (((−1)^(n+1) )/((2n+1)^2 )) = λ_0 ⇒ 2K =−(π/2)ln(2) +λ_0 ⇒K =−(π/4)ln(2) +(λ_0 /2) H =−(π/2)ln(2) −K =−(π/4)ln(2)−(λ_0 /2)
$$\left.\mathrm{2}\right)\:{let}\:{A}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:\: \\ $$$${A}=_{{t}={tan}\theta} \:\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\frac{{ln}\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right)}{\mathrm{1}+{tan}^{\mathrm{2}} \theta}\:\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right){d}\theta \\ $$$$=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\frac{\mathrm{1}}{{cos}^{\mathrm{2}} \theta}\right){d}\theta\:=−\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cos}\theta\right){d}\theta\:\: \\ $$$${let}\:{H}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cos}\theta\right){d}\theta\:\:{and}\:{K}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({sin}\theta\right){d}\theta \\ $$$${we}\:{have}\:\:{H}\:=_{\theta=\frac{\pi}{\mathrm{2}}−{t}} \:−\int_{\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{4}}} \:\:{ln}\left({sint}\right){dt} \\ $$$$=\:\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \:{ln}\left({sint}\right){dt}\:=\:−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({sint}\right){dt}\:+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({sint}\right){dt} \\ $$$$=−{K}\:−\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{2}\right)\:\Rightarrow\:{H}\:+{K}\:=−\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{2}\right)\: \\ $$$${K}−{H}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{ln}\left({sin}\theta\right){d}\theta\:−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cos}\theta\right){d}\theta \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({tan}\theta\right){d}\theta\:=_{{tan}\theta\:={u}} \:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{ln}\left({u}\right)}{\mathrm{1}+{u}^{\mathrm{2}} }\:{du} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} {u}^{\mathrm{2}{n}} \right){ln}\left({u}\right)\:{du} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\left(−\mathrm{1}\right)^{{n}} \:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{u}^{\mathrm{2}{n}} {ln}\left({u}\right){du}\:\:{by}\:{parts} \\ $$$${A}_{{n}} =\:\int_{\mathrm{0}} ^{\mathrm{1}} {u}^{\mathrm{2}{n}} {ln}\left({u}\right){du}\:=\:\left[\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}{u}^{\mathrm{2}{n}+\mathrm{1}} {ln}\left({u}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)}\:{u}^{\mathrm{2}{n}} {du}\:=−\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$${K}−{H}\:=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:\:=\:\lambda_{\mathrm{0}} \:\Rightarrow \\ $$$$\mathrm{2}{K}\:=−\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{2}\right)\:+\lambda_{\mathrm{0}} \:\Rightarrow{K}\:=−\frac{\pi}{\mathrm{4}}{ln}\left(\mathrm{2}\right)\:+\frac{\lambda_{\mathrm{0}} }{\mathrm{2}} \\ $$$${H}\:=−\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{2}\right)\:−{K}\:=−\frac{\pi}{\mathrm{4}}{ln}\left(\mathrm{2}\right)−\frac{\lambda_{\mathrm{0}} }{\mathrm{2}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *