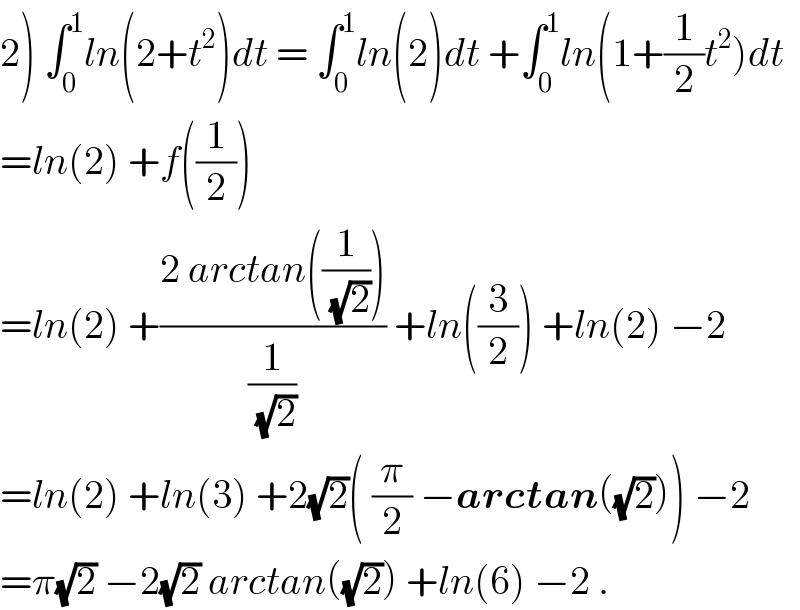Question Number 37343 by math khazana by abdo last updated on 12/Jun/18
$${let}\:{f}\left({x}\right)\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{xt}^{\mathrm{2}} \right){dt}\:\:{with}\:\mid{x}\mid<\mathrm{1} \\ $$$$\left.\mathrm{1}\right)\:{find}\:{f}\left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{2}+{t}^{\mathrm{2}} \right){dt}\:. \\ $$
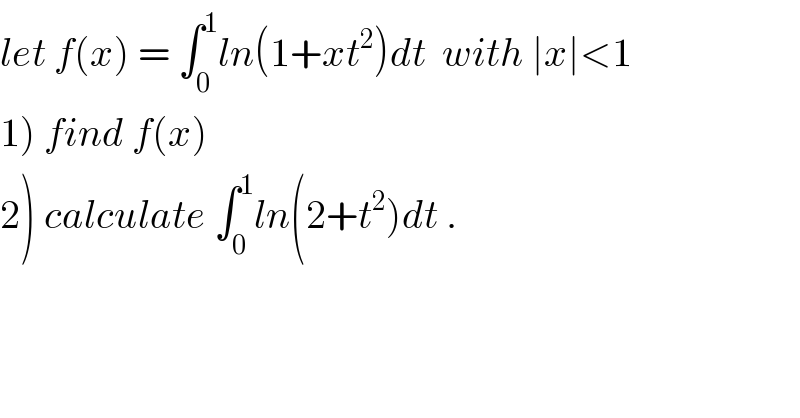
Commented by math khazana by abdo last updated on 15/Jun/18
![if −1<x<0 we get f(x) = (1/x) −(1/x) ∫_0 ^1 (dt/(1−(−x)t^2 )) and chanvement t(√(−x))=u give f^′ (x) = (1/x) −(1/x) ∫_0 ^(√(−x)) (1/(1−u^2 )) (du/( (√(−x)))) =(1/x) −(1/(x(√(−x)))) ∫_0 ^(√(−x)) (du/(1−u^2 )) =(1/x) −(1/(2x(√(−x)))) ∫_0 ^(√(−x)) { (1/(1−u )) +(1/(1+u))}du =(1/x) −(1/(2x(√(−x)))) [ln∣((1+u)/(1−u))∣]_0 ^(√(−x)) = (1/x) −(1/(2x(√(−x)))) ln∣ ((1+(√(−x)))/(1−(√(−x)))) ∣ ⇒ f(x) = ∫_(−1) ^x (dt/t) −∫_(−1) ^x (1/(2t(√(−t))))ln∣ ((1+(√(−t)))/(1−(√(−t))))∣ dt +c c =f(−1) = ∫_0 ^1 ln(1−t^2 )dt ⇒ f(x)=ln(−x) −∫_(−1) ^x (1/(2t(√(−t))))ln∣ ((1+(√(−t)))/(1−(√(−t))))∣ dt + ∫_0 ^1 ln(1−t^2 )dt . with−1<x<0 ....](https://www.tinkutara.com/question/Q37564.png)
$${if}\:−\mathrm{1}<{x}<\mathrm{0}\:\:{we}\:{get}\: \\ $$$${f}\left({x}\right)\:=\:\frac{\mathrm{1}}{{x}}\:−\frac{\mathrm{1}}{{x}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{dt}}{\mathrm{1}−\left(−{x}\right){t}^{\mathrm{2}} }\:\:{and}\:{chanvement} \\ $$$${t}\sqrt{−{x}}={u}\:{give} \\ $$$${f}^{'} \left({x}\right)\:=\:\frac{\mathrm{1}}{{x}}\:−\frac{\mathrm{1}}{{x}}\:\int_{\mathrm{0}} ^{\sqrt{−{x}}} \:\:\:\:\:\frac{\mathrm{1}}{\mathrm{1}−{u}^{\mathrm{2}} }\:\frac{{du}}{\:\sqrt{−{x}}} \\ $$$$=\frac{\mathrm{1}}{{x}}\:−\frac{\mathrm{1}}{{x}\sqrt{−{x}}}\:\int_{\mathrm{0}} ^{\sqrt{−{x}}} \:\:\frac{{du}}{\mathrm{1}−{u}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{{x}}\:−\frac{\mathrm{1}}{\mathrm{2}{x}\sqrt{−{x}}}\:\int_{\mathrm{0}} ^{\sqrt{−{x}}} \:\:\left\{\:\frac{\mathrm{1}}{\mathrm{1}−{u}\:}\:+\frac{\mathrm{1}}{\mathrm{1}+{u}}\right\}{du} \\ $$$$=\frac{\mathrm{1}}{{x}}\:−\frac{\mathrm{1}}{\mathrm{2}{x}\sqrt{−{x}}}\:\left[{ln}\mid\frac{\mathrm{1}+{u}}{\mathrm{1}−{u}}\mid\right]_{\mathrm{0}} ^{\sqrt{−{x}}} \\ $$$$=\:\frac{\mathrm{1}}{{x}}\:−\frac{\mathrm{1}}{\mathrm{2}{x}\sqrt{−{x}}}\:{ln}\mid\:\frac{\mathrm{1}+\sqrt{−{x}}}{\mathrm{1}−\sqrt{−{x}}}\:\mid\:\Rightarrow \\ $$$${f}\left({x}\right)\:=\:\int_{−\mathrm{1}} ^{{x}} \:\:\frac{{dt}}{{t}}\:\:−\int_{−\mathrm{1}} ^{{x}} \:\frac{\mathrm{1}}{\mathrm{2}{t}\sqrt{−{t}}}{ln}\mid\:\frac{\mathrm{1}+\sqrt{−{t}}}{\mathrm{1}−\sqrt{−{t}}}\mid\:{dt}\:+{c} \\ $$$${c}\:={f}\left(−\mathrm{1}\right)\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}−{t}^{\mathrm{2}} \right){dt}\:\Rightarrow \\ $$$${f}\left({x}\right)={ln}\left(−{x}\right)\:−\int_{−\mathrm{1}} ^{{x}} \:\:\frac{\mathrm{1}}{\mathrm{2}{t}\sqrt{−{t}}}{ln}\mid\:\frac{\mathrm{1}+\sqrt{−{t}}}{\mathrm{1}−\sqrt{−{t}}}\mid\:{dt} \\ $$$$+\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}−{t}^{\mathrm{2}} \right){dt}\:.\:{with}−\mathrm{1}<{x}<\mathrm{0}\:…. \\ $$$$ \\ $$
Commented by math khazana by abdo last updated on 15/Jun/18
![1) we have f^′ (x)^ = ∫_0 ^1 (t^2 /(1+xt^2 ))dt so if x≠0 f^′ (x)=(1/x) ∫_0 ^1 ((xt^2 +1−1)/(1+xt^2 ))dt =(1/x) −(1/x) ∫_0 ^1 (dt/(1+xt^2 )) for0<x<1 changement t(√x)=u give ∫_0 ^1 (dt/(1+xt^2 )) = ∫_0 ^(√x) (du/(1+u^2 )) (du/( (√x))) =(1/( (√x))) arctan((√x))⇒ f^′ (x) = (1/x) −((arctan((√x)))/(x(√x))) ⇒ f(x) = ∫_1 ^x (dt/t) −∫_1 ^x ((arctan((√t)))/(t(√t))) dt+c c=f(1) =∫_0 ^1 ln(1+t^2 )dt chang.(√t)=u give ∫_1 ^(x ) ((arctan((√t)))/(t(√t))) dt = ∫_1 ^(√x) ((arctan(u))/(u^2 .u)) 2u du =2 ∫_1 ^(√x) ((arctan(u))/u^2 ) du =2{ [−(1/u) arctan(u)]_1 ^(√x) −∫_1 ^(√x) −(1/u) (1/(1+u^2 ))du} =2{ (π/4) −((arctan((√x)))/( (√x))) } +2 ∫_1 ^(√x) (du/(u(1+u^2 ))) =(π/2) −((2arctan((√x)))/( (√x))) +2 ∫_1 ^(√x) ((1/u) −(u/(1+u^2 )))du =(π/2) −((2 arctan((√x)))/( (√x))) +2[ln((u/( (√(1+u^2 )))))]_1 ^(√x) =(π/2) −2((arctan((√x)))/( (√x))) +2 ln(((√x)/( (√(1+x))))) ⇒ f(x)=ln(x) −(π/2) +((2 arctan((√x)))/( (√x))) −2ln(((√x)/( (√(1+x))))) +∫_0 ^1 ln(1+t^2 )dt f(x)=ln(x) −(π/2) +((2arctan((√x)))/( (√x))) −lnx +ln(1+x) +∫_0 ^1 ln(1+t^2 )dt . and by parts ∫_0 ^1 ln(1+t^2 )dt = [t ln(1+t^2 )]_0 ^1 −∫_0 ^1 t ((2t)/(1+t^2 )) dt =ln(2) −2 ∫_0 ^1 ((t^2 +1−1)/(1+t^2 )) dt =ln(2) −2 +2 ∫_0 ^1 (dt/(1+t^2 )) =ln(2)−2 +(π/2) ⇒ f(x)= ((2 artan((√x)))/( (√x))) +ln(1+x) +ln(2)−2 with 0<x<1](https://www.tinkutara.com/question/Q37563.png)
$$\left.\mathrm{1}\right)\:{we}\:{have}\:{f}^{'} \left({x}\right)^{} \:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{t}^{\mathrm{2}} }{\mathrm{1}+{xt}^{\mathrm{2}} }{dt}\:{so}\:{if}\:{x}\neq\mathrm{0} \\ $$$${f}^{'} \left({x}\right)=\frac{\mathrm{1}}{{x}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{xt}^{\mathrm{2}} \:+\mathrm{1}−\mathrm{1}}{\mathrm{1}+{xt}^{\mathrm{2}} }{dt}\:=\frac{\mathrm{1}}{{x}}\:−\frac{\mathrm{1}}{{x}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{dt}}{\mathrm{1}+{xt}^{\mathrm{2}} }\:{for}\mathrm{0}<{x}<\mathrm{1} \\ $$$${changement}\:{t}\sqrt{{x}}={u}\:{give} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{dt}}{\mathrm{1}+{xt}^{\mathrm{2}} }\:=\:\int_{\mathrm{0}} ^{\sqrt{{x}}} \:\:\:\:\frac{{du}}{\mathrm{1}+{u}^{\mathrm{2}} }\:\frac{{du}}{\:\sqrt{{x}}}\:=\frac{\mathrm{1}}{\:\sqrt{{x}}}\:{arctan}\left(\sqrt{{x}}\right)\Rightarrow \\ $$$${f}^{'} \left({x}\right)\:=\:\frac{\mathrm{1}}{{x}}\:−\frac{{arctan}\left(\sqrt{{x}}\right)}{{x}\sqrt{{x}}}\:\:\Rightarrow \\ $$$${f}\left({x}\right)\:=\:\int_{\mathrm{1}} ^{{x}} \:\frac{{dt}}{{t}}\:\:−\int_{\mathrm{1}} ^{{x}} \:\:\:\frac{{arctan}\left(\sqrt{{t}}\right)}{{t}\sqrt{{t}}}\:{dt}+{c} \\ $$$${c}={f}\left(\mathrm{1}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right){dt}\:\:\:\:{chang}.\sqrt{{t}}={u}\:{give} \\ $$$$\int_{\mathrm{1}} ^{{x}\:\:} \:\:\frac{{arctan}\left(\sqrt{{t}}\right)}{{t}\sqrt{{t}}}\:{dt}\:=\:\int_{\mathrm{1}} ^{\sqrt{{x}}} \:\:\:\frac{{arctan}\left({u}\right)}{{u}^{\mathrm{2}} .{u}}\:\mathrm{2}{u}\:{du} \\ $$$$=\mathrm{2}\:\int_{\mathrm{1}} ^{\sqrt{{x}}} \:\:\frac{{arctan}\left({u}\right)}{{u}^{\mathrm{2}} }\:{du} \\ $$$$=\mathrm{2}\left\{\:\:\left[−\frac{\mathrm{1}}{{u}}\:{arctan}\left({u}\right)\right]_{\mathrm{1}} ^{\sqrt{{x}}} \:\:−\int_{\mathrm{1}} ^{\sqrt{{x}}} −\frac{\mathrm{1}}{{u}}\:\frac{\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{2}} }{du}\right\} \\ $$$$=\mathrm{2}\left\{\:\:\frac{\pi}{\mathrm{4}}\:−\frac{{arctan}\left(\sqrt{{x}}\right)}{\:\sqrt{{x}}}\:\right\}\:+\mathrm{2}\:\int_{\mathrm{1}} ^{\sqrt{{x}}} \:\:\:\frac{{du}}{{u}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)} \\ $$$$=\frac{\pi}{\mathrm{2}}\:\:−\frac{\mathrm{2}{arctan}\left(\sqrt{{x}}\right)}{\:\sqrt{{x}}}\:+\mathrm{2}\:\int_{\mathrm{1}} ^{\sqrt{{x}}} \:\left(\frac{\mathrm{1}}{{u}}\:−\frac{{u}}{\mathrm{1}+{u}^{\mathrm{2}} }\right){du} \\ $$$$=\frac{\pi}{\mathrm{2}}\:−\frac{\mathrm{2}\:{arctan}\left(\sqrt{{x}}\right)}{\:\sqrt{{x}}}\:+\mathrm{2}\left[{ln}\left(\frac{{u}}{\:\sqrt{\mathrm{1}+{u}^{\mathrm{2}} }}\right)\right]_{\mathrm{1}} ^{\sqrt{{x}}} \\ $$$$=\frac{\pi}{\mathrm{2}}\:−\mathrm{2}\frac{{arctan}\left(\sqrt{{x}}\right)}{\:\sqrt{{x}}}\:+\mathrm{2}\:{ln}\left(\frac{\sqrt{{x}}}{\:\sqrt{\mathrm{1}+{x}}}\right)\:\Rightarrow \\ $$$${f}\left({x}\right)={ln}\left({x}\right)\:−\frac{\pi}{\mathrm{2}}\:\:+\frac{\mathrm{2}\:{arctan}\left(\sqrt{{x}}\right)}{\:\sqrt{{x}}}\:−\mathrm{2}{ln}\left(\frac{\sqrt{{x}}}{\:\sqrt{\mathrm{1}+{x}}}\right) \\ $$$$+\int_{\mathrm{0}} ^{\mathrm{1}} \:{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right){dt} \\ $$$${f}\left({x}\right)={ln}\left({x}\right)\:−\frac{\pi}{\mathrm{2}}\:+\frac{\mathrm{2}{arctan}\left(\sqrt{{x}}\right)}{\:\sqrt{{x}}}\:−{lnx}\:+{ln}\left(\mathrm{1}+{x}\right) \\ $$$$+\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right){dt}\:\:\:.\:{and}\:{by}\:{parts} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right){dt}\:=\:\left[{t}\:{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{t}\:\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\:{dt} \\ $$$$={ln}\left(\mathrm{2}\right)\:−\mathrm{2}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{t}^{\mathrm{2}} \:+\mathrm{1}−\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }\:{dt} \\ $$$$={ln}\left(\mathrm{2}\right)\:−\mathrm{2}\:\:+\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:={ln}\left(\mathrm{2}\right)−\mathrm{2}\:\:+\frac{\pi}{\mathrm{2}}\:\Rightarrow \\ $$$${f}\left({x}\right)=\:\frac{\mathrm{2}\:{artan}\left(\sqrt{{x}}\right)}{\:\sqrt{{x}}}\:+{ln}\left(\mathrm{1}+{x}\right)\:+{ln}\left(\mathrm{2}\right)−\mathrm{2} \\ $$$${with}\:\mathrm{0}<{x}<\mathrm{1} \\ $$
Commented by math khazana by abdo last updated on 15/Jun/18
$$\left.\mathrm{2}\right)\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{2}+{t}^{\mathrm{2}} \right){dt}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{2}\right){dt}\:+\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}{t}^{\mathrm{2}} \right){dt} \\ $$$$={ln}\left(\mathrm{2}\right)\:+{f}\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$={ln}\left(\mathrm{2}\right)\:+\frac{\mathrm{2}\:{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)}{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}\:+{ln}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\:+{ln}\left(\mathrm{2}\right)\:−\mathrm{2} \\ $$$$={ln}\left(\mathrm{2}\right)\:+{ln}\left(\mathrm{3}\right)\:+\mathrm{2}\sqrt{\mathrm{2}}\left(\:\frac{\pi}{\mathrm{2}}\:−\boldsymbol{{arctan}}\left(\sqrt{\mathrm{2}}\right)\right)\:−\mathrm{2} \\ $$$$=\pi\sqrt{\mathrm{2}}\:−\mathrm{2}\sqrt{\mathrm{2}}\:{arctan}\left(\sqrt{\mathrm{2}}\right)\:+{ln}\left(\mathrm{6}\right)\:−\mathrm{2}\:. \\ $$