Question Number 38310 by maxmathsup by imad last updated on 23/Jun/18
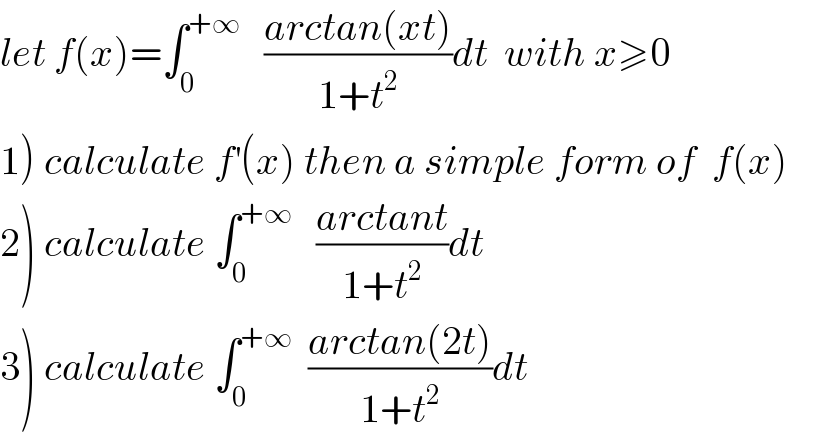
$${let}\:{f}\left({x}\right)=\int_{\mathrm{0}} ^{+\infty} \:\:\:\frac{{arctan}\left({xt}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:\:{with}\:{x}\geqslant\mathrm{0} \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:{f}^{'} \left({x}\right)\:{then}\:{a}\:{simple}\:{form}\:{of}\:\:{f}\left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\int_{\mathrm{0}} ^{+\infty} \:\:\:\frac{{arctant}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$$\left.\mathrm{3}\right)\:{calculate}\:\int_{\mathrm{0}} ^{+\infty} \:\:\frac{{arctan}\left(\mathrm{2}{t}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$
Commented by prof Abdo imad last updated on 24/Jun/18

$$\left.\mathrm{1}\right){we}\:{have}\:{f}^{'} \left({x}\right)=\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\:\:\:\:\frac{{t}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left(\mathrm{1}+{x}^{\mathrm{2}} {t}^{\mathrm{2}} \right)}{dt} \\ $$$${let}\:{decompose}\:{F}\left({t}\right)=\:\frac{{t}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left(\mathrm{1}+{x}^{\mathrm{2}} {t}^{\mathrm{2}} \right)} \\ $$$${F}\left({t}\right)=\:\frac{{at}\:+{b}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{{ct}\:+{d}}{{x}^{\mathrm{2}} {t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${F}\left(−{t}\right)=−{F}\left({t}\right)\Rightarrow\frac{−{at}\:+{b}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{−{ct}\:+{d}}{{x}^{\mathrm{2}} {t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$=\frac{−{at}−{b}}{{t}^{\mathrm{2}} +\mathrm{1}}\:\:+\frac{−{ct}−{d}}{{x}^{\mathrm{2}} {t}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow{n}={d}=\mathrm{0}\:\Rightarrow \\ $$$${F}\left({t}\right)=\:\:\frac{{at}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{{ct}}{{x}^{\mathrm{2}} {t}^{\mathrm{2}\:} +\mathrm{1}} \\ $$$${lim}_{{t}\rightarrow+\infty} {t}\:{F}\left({t}\right)=\mathrm{0}={a}\:+\frac{{c}}{{x}^{\mathrm{2}} }\:\Rightarrow{ax}^{\mathrm{2}} +{c}=\mathrm{0}\:\Rightarrow \\ $$$${c}=−{ax}^{\mathrm{2}} \:\Rightarrow{F}\left({t}\right)=\:\frac{{at}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:−{x}^{\mathrm{2}} \:\:\frac{{at}}{{x}^{\mathrm{2}} {t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${F}\left(\mathrm{1}\right)=\:\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}\:=\:\:\frac{{a}}{\mathrm{2}}\:−\frac{{ax}^{\mathrm{2}} }{{x}^{\mathrm{2}} +\mathrm{1}}\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\:=\:\frac{\mathrm{1}+{x}^{\mathrm{2}} }{\mathrm{2}}{a}\:−{ax}^{\mathrm{2}} \:=\frac{\mathrm{1}+{x}^{\mathrm{2}} \:−\mathrm{2}{x}^{\mathrm{2}} }{\mathrm{2}}{a}\:=\frac{\mathrm{1}−{x}^{\mathrm{2}} }{\mathrm{2}}{a}\:\Rightarrow \\ $$$$\left(\mathrm{1}−{x}^{\mathrm{2}} \right){a}=\mathrm{1}\:\Rightarrow{a}=\:\frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} }\:\:{if}\:{x}^{\mathrm{2}} \neq\mathrm{1}\:\Rightarrow \\ $$$${F}\left({x}\right)=\:\frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} }\:\:\frac{{t}}{{t}^{\mathrm{2}} +\mathrm{1}}\:−\frac{{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} }\:\:\frac{{t}}{{x}^{\mathrm{2}} {t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} }\left\{\:\:\:\frac{{t}}{{t}^{\mathrm{2}} +\mathrm{1}}\:−\:\frac{{x}^{\mathrm{2}} {t}}{{x}^{\mathrm{2}} {t}^{\mathrm{2}} +\mathrm{1}}\right\}\:. \\ $$
Commented by abdo.msup.com last updated on 24/Jun/18
![f^, (x)=∫_0 ^∞ F(t)dt ⇒(1−x^2 )f^′ (x) = ∫_0 ^∞ (t/(1+t^2 ))dt −(1/2)∫_0 ^∞ ((2x^2 t)/(x^2 t^2 +1))dt =[(1/2)ln∣ ((1+t^2 )/(x^2 t^2 +1))∣]_0 ^(+∞) =(1/2)ln((1/x^2 ))=−ln∣x∣ ⇒f^′ (x)=−((ln∣x∣)/(1−x^2 ))](https://www.tinkutara.com/question/Q38378.png)
$${f}^{,} \left({x}\right)=\int_{\mathrm{0}} ^{\infty} \:{F}\left({t}\right){dt}\:\Rightarrow\left(\mathrm{1}−{x}^{\mathrm{2}} \right){f}^{'} \left({x}\right) \\ $$$$=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{t}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:\:−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{2}{x}^{\mathrm{2}} {t}}{{x}^{\mathrm{2}} {t}^{\mathrm{2}} \:+\mathrm{1}}{dt} \\ $$$$\:=\left[\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\:\:\frac{\mathrm{1}+{t}^{\mathrm{2}} }{{x}^{\mathrm{2}} {t}^{\mathrm{2}} +\mathrm{1}}\mid\right]_{\mathrm{0}} ^{+\infty} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)=−{ln}\mid{x}\mid\:\Rightarrow{f}^{'} \left({x}\right)=−\frac{{ln}\mid{x}\mid}{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$
Commented by abdo.msup.com last updated on 24/Jun/18
![for x>0 we get f^′ (x)=−((ln(x))/(1−x^2 )) ⇒ f(x)= −∫_1 ^x ((ln(t))/(1−t^2 ))dt +c c=f(1)= ∫_0 ^∞ ((arctant)/(1+t^2 ))dt changement t=tanθ give f(1)= ∫_0 ^(π/2) (θ/(1+tan^2 θ)) (1+tan^2 θ)dθ =∫_0 ^(π/2) θ dθ=[(θ^2 /2)]_0 ^(π/2) =(π^2 /8) ⇒ f(x)=(π^2 /8) −∫_1 ^x ((ln(t))/(1−t^2 ))dt .](https://www.tinkutara.com/question/Q38379.png)
$${for}\:{x}>\mathrm{0}\:{we}\:{get}\:{f}^{'} \left({x}\right)=−\frac{{ln}\left({x}\right)}{\mathrm{1}−{x}^{\mathrm{2}} }\:\Rightarrow \\ $$$${f}\left({x}\right)=\:−\int_{\mathrm{1}} ^{{x}} \:\frac{{ln}\left({t}\right)}{\mathrm{1}−{t}^{\mathrm{2}} }{dt}\:+{c} \\ $$$${c}={f}\left(\mathrm{1}\right)=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{arctant}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:{changement} \\ $$$${t}={tan}\theta\:{give} \\ $$$${f}\left(\mathrm{1}\right)=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{\theta}{\mathrm{1}+{tan}^{\mathrm{2}} \theta}\:\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right){d}\theta \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\theta\:{d}\theta=\left[\frac{\theta^{\mathrm{2}} }{\mathrm{2}}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} =\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:\Rightarrow \\ $$$${f}\left({x}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:−\int_{\mathrm{1}} ^{{x}} \:\:\frac{{ln}\left({t}\right)}{\mathrm{1}−{t}^{\mathrm{2}} }{dt}\:. \\ $$
Commented by prof Abdo imad last updated on 24/Jun/18
![2) ∫_0 ^∞ ((arctan(t))/(1+t^2 ))dt =(π^2 /8) 3) ∫_0 ^∞ ((arctan(2t))/(1+t^2 ))dt =f(2) =(π^2 /8) −∫_1 ^2 ((ln(t))/(1−t^2 ))dt changement t=1+x give ∫_1 ^2 ((ln(t))/(1−t^2 ))dt = ∫_0 ^1 ((ln(1+x))/(1−(1+x)^2 ))dx =∫_0 ^1 ((ln(1+x))/(1−1−x^2 −2x))dx = −∫_0 ^1 ((ln(1+x))/(x(x+2)))dx =−∫_0 ^1 ln(1+x)((1/x) −(1/(x+2)))dx =−(1/2) ∫_0 ^1 ( ((ln(1+x))/x) −((ln(1+x))/(x+2)))dx =(1/2) ∫_0 ^1 ((ln(1+x))/(x+2))dx −(1/2) ∫_0 ^1 ((ln(1+x))/x)dx but ln^′ (1+x) = (1/(1+x)) =Σ_(n=0) ^∞ (−1)^n x^n ⇒ ln(1+x)=Σ_(n=0) ^∞ (((−1)^n )/(n+1))x^(n+1) =Σ_(n=1) ^∞ (((−1)^(n−1) )/n)x^n ⇒∫_0 ^1 ((ln(1+x))/x)dx=∫_0 ^1 (Σ_(n=1) ^∞ (((−1)^(n−1) )/n)x^(n−1) ) =Σ_(n=1) ^∞ (((−1)^(n−1) )/n^ )∫_0 ^1 x^(n−1) dx =−Σ_(n=1) ^∞ (((−1)^n )/n^2 ) =−(−(π^2 /(12)))=(π^2 /(12)) by parts ∫_0 ^1 ((ln(1+x))/(x+2))dx =[ln(1+x)ln(2+x)]_0 ^1 −∫_0 ^1 ((ln(x+2))/(x+1))dx =ln(2)ln(3)−∫_0 ^1 ((ln(x+2))/(x+1))dx ∫_0 ^1 ((ln(x+2))/(x+1))dx=∫_0 ^1 (Σ_(n=0) ^∞ (−1)^n x^n )ln(x+2)dx =Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 x^n ln(x+2)dx by parts A_n = ∫_0 ^1 x^n ln(x+2)dx =[(1/(n+1))x^(n+1) ln(x+2)]_0 ^1 −∫_0 ^1 (x^(n+1) /((n+1)(x+2)))dx =(1/(n+1)){ln(3) −2^(n+1) ln(2)}−(1/(n+1)) ∫_0 ^1 (x^(n+1) /(x+2))dx ...be continued...](https://www.tinkutara.com/question/Q38382.png)
$$\left.\mathrm{2}\right)\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{arctan}\left({t}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{8}} \\ $$$$\left.\mathrm{3}\right)\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{arctan}\left(\mathrm{2}{t}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:={f}\left(\mathrm{2}\right) \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:−\int_{\mathrm{1}} ^{\mathrm{2}} \:\:\frac{{ln}\left({t}\right)}{\mathrm{1}−{t}^{\mathrm{2}} }{dt}\:{changement} \\ $$$${t}=\mathrm{1}+{x}\:{give} \\ $$$$\int_{\mathrm{1}} ^{\mathrm{2}} \:\:\:\frac{{ln}\left({t}\right)}{\mathrm{1}−{t}^{\mathrm{2}} }{dt}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{ln}\left(\mathrm{1}+{x}\right)}{\mathrm{1}−\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{ln}\left(\mathrm{1}+{x}\right)}{\mathrm{1}−\mathrm{1}−{x}^{\mathrm{2}} −\mathrm{2}{x}}{dx} \\ $$$$=\:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{ln}\left(\mathrm{1}+{x}\right)}{{x}\left({x}+\mathrm{2}\right)}{dx} \\ $$$$=−\int_{\mathrm{0}} ^{\mathrm{1}} \:{ln}\left(\mathrm{1}+{x}\right)\left(\frac{\mathrm{1}}{{x}}\:−\frac{\mathrm{1}}{{x}+\mathrm{2}}\right){dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \left(\:\frac{{ln}\left(\mathrm{1}+{x}\right)}{{x}}\:−\frac{{ln}\left(\mathrm{1}+{x}\right)}{{x}+\mathrm{2}}\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}+{x}\right)}{{x}+\mathrm{2}}{dx}\:−\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{ln}\left(\mathrm{1}+{x}\right)}{{x}}{dx}\:{but} \\ $$$${ln}^{'} \left(\mathrm{1}+{x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{1}+{x}}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} {x}^{{n}} \:\Rightarrow \\ $$$${ln}\left(\mathrm{1}+{x}\right)=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}+\mathrm{1}}{x}^{{n}+\mathrm{1}} =\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}{x}^{{n}} \\ $$$$\:\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{ln}\left(\mathrm{1}+{x}\right)}{{x}}{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}{x}^{{n}−\mathrm{1}} \right) \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}^{} }\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{{n}−\mathrm{1}} {dx} \\ $$$$=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{2}} }\:=−\left(−\frac{\pi^{\mathrm{2}} }{\mathrm{12}}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$$${by}\:{parts}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{x}\right)}{{x}+\mathrm{2}}{dx} \\ $$$$=\left[{ln}\left(\mathrm{1}+{x}\right){ln}\left(\mathrm{2}+{x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:\:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{ln}\left({x}+\mathrm{2}\right)}{{x}+\mathrm{1}}{dx} \\ $$$$={ln}\left(\mathrm{2}\right){ln}\left(\mathrm{3}\right)−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{ln}\left({x}+\mathrm{2}\right)}{{x}+\mathrm{1}}{dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{ln}\left({x}+\mathrm{2}\right)}{{x}+\mathrm{1}}{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} {x}^{{n}} \right){ln}\left({x}+\mathrm{2}\right){dx} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\left(−\mathrm{1}\right)^{{n}} \:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{{n}} {ln}\left({x}+\mathrm{2}\right){dx}\:{by}\:{parts} \\ $$$${A}_{{n}} =\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{{n}} {ln}\left({x}+\mathrm{2}\right){dx} \\ $$$$=\left[\frac{\mathrm{1}}{{n}+\mathrm{1}}{x}^{{n}+\mathrm{1}} {ln}\left({x}+\mathrm{2}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{x}^{{n}+\mathrm{1}} }{\left({n}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)}{dx} \\ $$$$=\frac{\mathrm{1}}{{n}+\mathrm{1}}\left\{{ln}\left(\mathrm{3}\right)\:−\mathrm{2}^{{n}+\mathrm{1}} {ln}\left(\mathrm{2}\right)\right\}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{x}^{{n}+\mathrm{1}} }{{x}+\mathrm{2}}{dx} \\ $$$$…{be}\:{continued}… \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 24/Jun/18
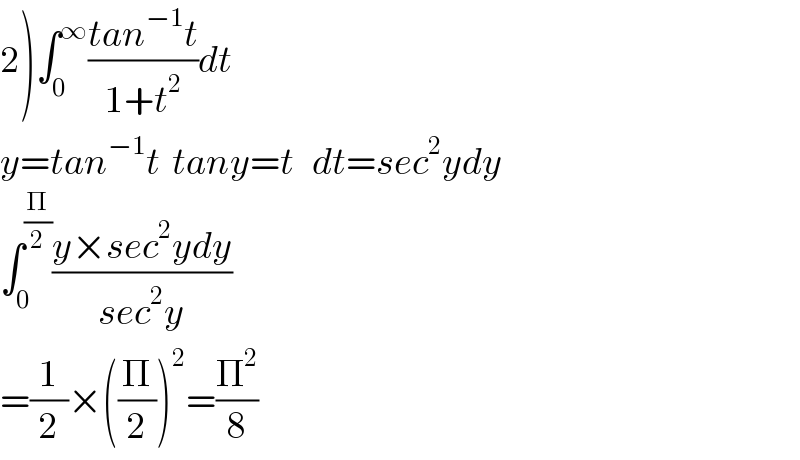
$$\left.\mathrm{2}\right)\int_{\mathrm{0}} ^{\infty} \frac{{tan}^{−\mathrm{1}} {t}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$${y}={tan}^{−\mathrm{1}} {t}\:\:{tany}={t}\:\:\:{dt}={sec}^{\mathrm{2}} {ydy} \\ $$$$\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} \frac{{y}×{sec}^{\mathrm{2}} {ydy}}{{sec}^{\mathrm{2}} {y}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\left(\frac{\Pi}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{\prod^{\mathrm{2}} }{\mathrm{8}} \\ $$
