Question Number 98184 by abdomathmax last updated on 12/Jun/20
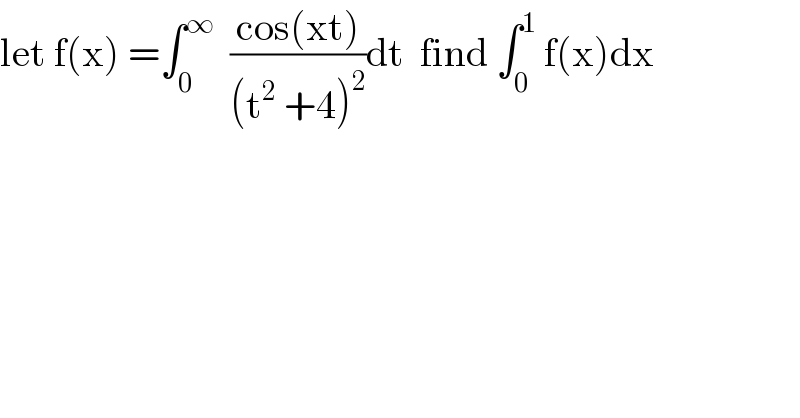
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{cos}\left(\mathrm{xt}\right)}{\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{4}\right)^{\mathrm{2}} }\mathrm{dt}\:\:\mathrm{find}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx} \\ $$
Answered by mathmax by abdo last updated on 12/Jun/20
![f(x) =∫_0 ^∞ ((cos(xt))/((t^2 +4)^2 ))dt ⇒f(x) =_(t=2u) ∫_0 ^∞ ((cos(2xu))/(16(u^2 +1)^2 )) ×2du =(1/8) ∫_0 ^∞ ((cos(2xu))/((u^2 +1)^2 ))du =(1/(16))∫_(−∞) ^(+∞) ((cos(2xu))/((u^2 +1)^2 ))du ⇒16f(x) =Re(∫_(−∞) ^(+∞) (e^(2xiu) /((u^2 +1)^2 ))du) let ϕ(z) =(e^(2xiz) /((z^2 +1)^2 )) ⇒ϕ(z) =(e^(2xiz) /((z−i)^2 (z+i)^2 )) residus theorem give ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ Res(ϕ,i) Res(ϕ,i) =lim_(z→i) (1/((2−1)!)){ (z−i)^2 ϕ(z)}^((1)) =lim_(z→i) { (e^(2xiz) /((z+i)^2 ))}^((1)) =lim_(z→i) ((2xi e^(2xiz) (z+i)^2 −2(z+i)e^(2xiz) )/((z+i)^4 )) =lim_(z→i) (((2xi(z+i)−2}e^(2xiz) )/((z+i)^3 )) =(({2i(2xi)−2}e^(−2x) )/((2i)^3 )) =(({−4x−2}e^(−2x) )/(−8i)) =(({2x+1)e^(−2x) )/(4i)) ⇒∫_(−∞) ^(+∞) ϕ(z)dz =2iπ×(((2x+1)e^(−2x) )/(4i)) =(π/2)(2x+1)e^(−2x) ⇒f(x) =(π/(32))(2x+1)e^(−2x) ⇒ ∫_0 ^1 f(x)dx =(π/(32)) ∫_0 ^1 (2x+1)e^(−2x) dx by parts ∫_0 ^1 (2x+1)e^(−2x) dx =[((2x+1)/(−2)) e^(−2x) ]_0 ^1 −∫_0 ^1 (2/(−2)) e^(−2x) dx =−(1/2)( 3e^(−2) −1) +∫_0 ^1 e^(−2x) dx =−(3/2)e^(−2) +(1/2) +[−(1/2)e^(−2x) ]_0 ^1 =−(3/(2e^2 )) +(1/2)−(1/2)( (1/e^2 )−1) =−(3/(2e^2 ))−(1/(2e^2 )) +1 =1−(2/e^2 ) ⇒ ∫_0 ^1 f(x)dx =(π/(32))(1−(2/e^2 ))](https://www.tinkutara.com/question/Q98239.png)
$$\mathrm{f}\left(\mathrm{x}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{cos}\left(\mathrm{xt}\right)}{\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{4}\right)^{\mathrm{2}} }\mathrm{dt}\:\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=_{\mathrm{t}=\mathrm{2u}} \:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{cos}\left(\mathrm{2xu}\right)}{\mathrm{16}\left(\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:×\mathrm{2du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{cos}\left(\mathrm{2xu}\right)}{\left(\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{du}\:=\frac{\mathrm{1}}{\mathrm{16}}\int_{−\infty} ^{+\infty} \:\frac{\mathrm{cos}\left(\mathrm{2xu}\right)}{\left(\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{du}\:\Rightarrow\mathrm{16f}\left(\mathrm{x}\right)\:=\mathrm{Re}\left(\int_{−\infty} ^{+\infty} \:\frac{\mathrm{e}^{\mathrm{2xiu}} }{\left(\mathrm{u}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\mathrm{du}\right) \\ $$$$\mathrm{let}\:\varphi\left(\mathrm{z}\right)\:=\frac{\mathrm{e}^{\mathrm{2xiz}} }{\left(\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow\varphi\left(\mathrm{z}\right)\:=\frac{\mathrm{e}^{\mathrm{2xiz}} }{\left(\mathrm{z}−\mathrm{i}\right)^{\mathrm{2}} \left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{2}} }\:\:\mathrm{residus}\:\mathrm{theorem}\:\mathrm{give} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\:\mathrm{Res}\left(\varphi,\mathrm{i}\right) \\ $$$$\mathrm{Res}\left(\varphi,\mathrm{i}\right)\:=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{1}\right)!}\left\{\:\left(\mathrm{z}−\mathrm{i}\right)^{\mathrm{2}} \varphi\left(\mathrm{z}\right)\right\}^{\left(\mathrm{1}\right)} \:=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\left\{\:\frac{\mathrm{e}^{\mathrm{2xiz}} }{\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{2}} }\right\}^{\left(\mathrm{1}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\:\:\frac{\mathrm{2xi}\:\mathrm{e}^{\mathrm{2xiz}} \left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{2}} −\mathrm{2}\left(\mathrm{z}+\mathrm{i}\right)\mathrm{e}^{\mathrm{2xiz}} }{\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{4}} } \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\:\:\:\frac{\left(\mathrm{2xi}\left(\mathrm{z}+\mathrm{i}\right)−\mathrm{2}\right\}\mathrm{e}^{\mathrm{2xiz}} }{\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{3}} }\:=\frac{\left\{\mathrm{2i}\left(\mathrm{2xi}\right)−\mathrm{2}\right\}\mathrm{e}^{−\mathrm{2x}} }{\left(\mathrm{2i}\right)^{\mathrm{3}} }\:=\frac{\left\{−\mathrm{4x}−\mathrm{2}\right\}\mathrm{e}^{−\mathrm{2x}} }{−\mathrm{8i}} \\ $$$$=\frac{\left\{\mathrm{2x}+\mathrm{1}\right)\mathrm{e}^{−\mathrm{2x}} }{\mathrm{4i}}\:\Rightarrow\int_{−\infty} ^{+\infty} \:\varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi×\frac{\left(\mathrm{2x}+\mathrm{1}\right)\mathrm{e}^{−\mathrm{2x}} }{\mathrm{4i}}\:=\frac{\pi}{\mathrm{2}}\left(\mathrm{2x}+\mathrm{1}\right)\mathrm{e}^{−\mathrm{2x}} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\pi}{\mathrm{32}}\left(\mathrm{2x}+\mathrm{1}\right)\mathrm{e}^{−\mathrm{2x}} \:\Rightarrow\:\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}\:=\frac{\pi}{\mathrm{32}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\left(\mathrm{2x}+\mathrm{1}\right)\mathrm{e}^{−\mathrm{2x}} \:\mathrm{dx}\:\:\mathrm{by}\:\mathrm{parts} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\left(\mathrm{2x}+\mathrm{1}\right)\mathrm{e}^{−\mathrm{2x}} \:\mathrm{dx}\:=\left[\frac{\mathrm{2x}+\mathrm{1}}{−\mathrm{2}}\:\:\mathrm{e}^{−\mathrm{2x}} \right]_{\mathrm{0}} ^{\mathrm{1}} \:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{2}}{−\mathrm{2}}\:\mathrm{e}^{−\mathrm{2x}} \:\mathrm{dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\left(\:\mathrm{3e}^{−\mathrm{2}} −\mathrm{1}\right)\:+\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{e}^{−\mathrm{2x}} \:\mathrm{dx}\:=−\frac{\mathrm{3}}{\mathrm{2}}\mathrm{e}^{−\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\:+\left[−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{−\mathrm{2x}} \right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=−\frac{\mathrm{3}}{\mathrm{2e}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\left(\:\frac{\mathrm{1}}{\mathrm{e}^{\mathrm{2}} }−\mathrm{1}\right)\:=−\frac{\mathrm{3}}{\mathrm{2e}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2e}^{\mathrm{2}} }\:+\mathrm{1}\:=\mathrm{1}−\frac{\mathrm{2}}{\mathrm{e}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}\:=\frac{\pi}{\mathrm{32}}\left(\mathrm{1}−\frac{\mathrm{2}}{\mathrm{e}^{\mathrm{2}} }\right) \\ $$
