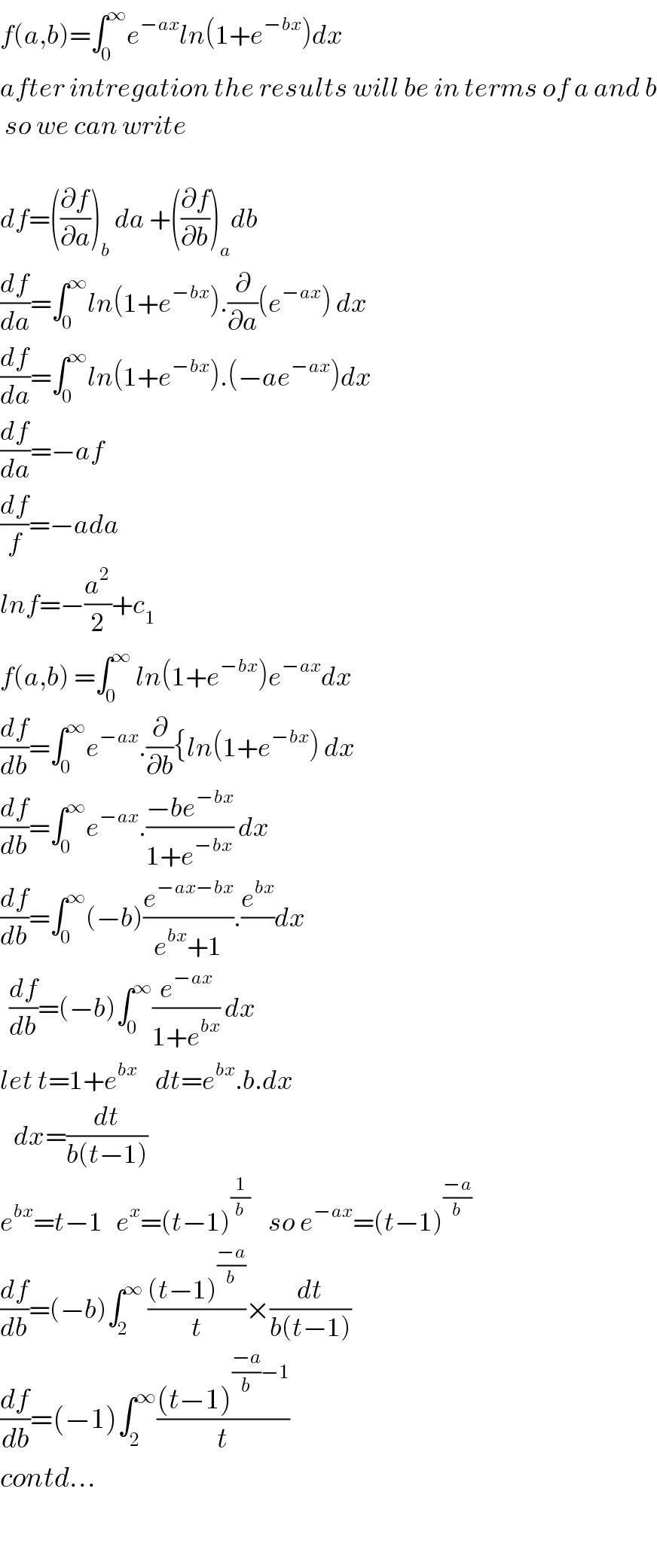Menu Close

let-f-x-0-e-ax-ln-1-e-bx-dx-with-a-gt-0-and-b-gt-0-1-calculate-f-a-x-2-calculate-f-b-x-3-find-the-value-of-0-e-2x-ln-1-e-x-dx-and-0-e-x-ln-1-e-2x-

Tinku Tara 0 Comments
Pin




Question Number 41301 by math khazana by abdo last updated on 05/Aug/18
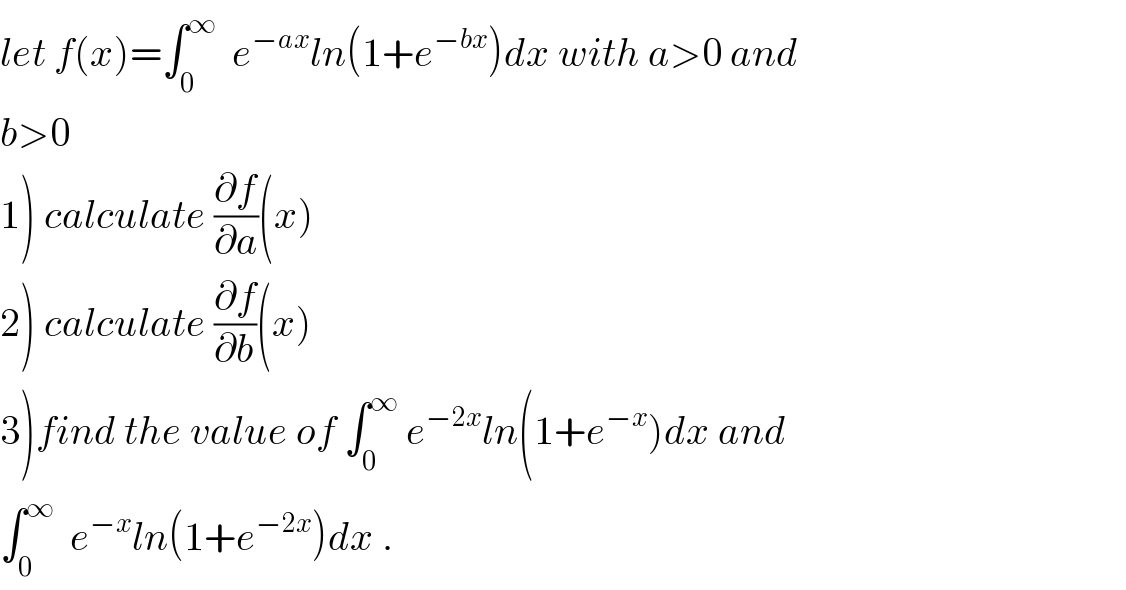
let f(x)=∫_0 ^∞ e^(−ax) ln(1+e^(−bx) )dx with a>0 and b>0 1) calculate (∂f/∂a)(x) 2) calculate (∂f/∂b)(x) 3)find the value of ∫_0 ^∞ e^(−2x) ln(1+e^(−x) )dx and ∫_0 ^∞ e^(−x) ln(1+e^(−2x) )dx .
$${let}\:{f}\left({x}\right)=\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{ax}} {ln}\left(\mathrm{1}+{e}^{−{bx}} \right){dx}\:{with}\:{a}>\mathrm{0}\:{and} \\ $$$${b}>\mathrm{0} \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:\frac{\partial{f}}{\partial{a}}\left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\frac{\partial{f}}{\partial{b}}\left({x}\right) \\ $$$$\left.\mathrm{3}\right){find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−\mathrm{2}{x}} {ln}\left(\mathrm{1}+{e}^{−{x}} \right){dx}\:{and} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{x}} {ln}\left(\mathrm{1}+{e}^{−\mathrm{2}{x}} \right){dx}\:. \\ $$
Commented by prof Abdo imad last updated on 05/Aug/18
1) we have (∂f/∂a)(x)=−∫_0 ^∞ xe^(−ax) ln(1+e^(−bx) )dx but for ∣u∣<1 ln(1+u)=Σ_(n=1) ^∞ (((−1)^(n−1) u^n )/n) ⇒ (∂f/∂a)(x) =−∫_0 ^∞ x^ e^(−ax) (Σ_(n=1) ^∞ (((−1)^(n−1) )/n) e^(−nbx) )dx =Σ_(n=1) ^∞ (((−1)^n )/n) ∫_0 ^∞ xe^(−(a+nb)x) dx by parts A_n =∫_0 ^∞ x e^(−(a+nb)x) dx =[((−x)/(a+nb)) e^(−(a+nb)x) ]_0 ^(+∞) −∫_0 ^∞ −(1/(a+nb)) e^(−(a+nb)x) dx =(1/(a+nb)) ∫_0 ^∞ e^(−(a+nb)x) dx =−(1/(a+nb))[ (1/(a+nb))]_0 ^(+∞) = (1/((a+nb)^2 )) ⇒(∂f/∂a)(x)=Σ_(n=1) ^∞ (((−1)^n )/(n(a+nb)^2 )) ...
$$\left.\mathrm{1}\right)\:{we}\:{have}\:\frac{\partial{f}}{\partial{a}}\left({x}\right)=−\int_{\mathrm{0}} ^{\infty} \:{xe}^{−{ax}} {ln}\left(\mathrm{1}+{e}^{−{bx}} \right){dx} \\ $$$${but}\:{for}\:\mid{u}\mid<\mathrm{1}\:\:{ln}\left(\mathrm{1}+{u}\right)=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} {u}^{{n}} }{{n}}\:\Rightarrow \\ $$$$\frac{\partial{f}}{\partial{a}}\left({x}\right)\:=−\int_{\mathrm{0}} ^{\infty} \:\:{x}^{} \:{e}^{−{ax}} \left(\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:{e}^{−{nbx}} \right){dx} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}}\:\:\int_{\mathrm{0}} ^{\infty} \:{xe}^{−\left({a}+{nb}\right){x}} {dx}\:{by}\:{parts} \\ $$$${A}_{{n}} =\int_{\mathrm{0}} ^{\infty} \:\:{x}\:{e}^{−\left({a}+{nb}\right){x}} {dx}\:=\left[\frac{−{x}}{{a}+{nb}}\:{e}^{−\left({a}+{nb}\right){x}} \right]_{\mathrm{0}} ^{+\infty} \\ $$$$−\int_{\mathrm{0}} ^{\infty} \:\:−\frac{\mathrm{1}}{{a}+{nb}}\:{e}^{−\left({a}+{nb}\right){x}} {dx} \\ $$$$=\frac{\mathrm{1}}{{a}+{nb}}\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−\left({a}+{nb}\right){x}} {dx}\:=−\frac{\mathrm{1}}{{a}+{nb}}\left[\:\frac{\mathrm{1}}{{a}+{nb}}\right]_{\mathrm{0}} ^{+\infty} \\ $$$$=\:\frac{\mathrm{1}}{\left({a}+{nb}\right)^{\mathrm{2}} }\:\Rightarrow\frac{\partial{f}}{\partial{a}}\left({x}\right)=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}\left({a}+{nb}\right)^{\mathrm{2}} }\:… \\ $$
Commented by prof Abdo imad last updated on 05/Aug/18
2) we have (∂f/∂b)(x)=−∫_0 ^∞ e^(−ax) (x/(1+e^(−bx) ))dx =−∫_0 ^∞ x e^(−ax) (Σ_(n=0) ^∞ (−1)^n e^(−nbx) )dx =Σ_(n=0) ^∞ (−1)^(n+1) ∫_0 ^∞ x e^(−(a+nb)x) dx but we have proved that ∫_0 ^∞ x e^(−(a+nb)x) dx =(1/((a+nb)^2 )) ⇒ (∂f/∂b)(x) =Σ_(n=0) ^∞ (((−1)^(n+1) )/((a+nb)^2 )) ...
$$\left.\mathrm{2}\right)\:{we}\:{have}\:\frac{\partial{f}}{\partial{b}}\left({x}\right)=−\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{ax}} \:\frac{{x}}{\mathrm{1}+{e}^{−{bx}} }{dx} \\ $$$$=−\int_{\mathrm{0}} ^{\infty} \:\:{x}\:{e}^{−{ax}} \left(\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} \:{e}^{−{nbx}} \right){dx} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \:\int_{\mathrm{0}} ^{\infty} {x}\:{e}^{−\left({a}+{nb}\right){x}} {dx}\:{but}\:{we}\:{have} \\ $$$${proved}\:{that}\:\int_{\mathrm{0}} ^{\infty} \:\:{x}\:{e}^{−\left({a}+{nb}\right){x}} {dx}\:\:=\frac{\mathrm{1}}{\left({a}+{nb}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\frac{\partial{f}}{\partial{b}}\left({x}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{\left({a}+{nb}\right)^{\mathrm{2}} }\:… \\ $$
Commented by prof Abdo imad last updated on 05/Aug/18
3)let I = ∫_0 ^∞ e^(−2x) ln(1+e^(−x)) dx I = ∫_0 ^∞ e^(−2x) (Σ_(n=1) ^∞ (((−1)^(n−1) )/n) e^(−nx) )dx =Σ_(n=1) ^∞ (((−1)^(n−1) )/n) ∫_0 ^∞ e^(−(n+2)x) dx but ∫_0 ^∞ e^(−(n+2)x) dx=[((−1)/(n+2)) e^(−(n+2)x) ]_0 ^(+∞) =(1/(n+2)) ⇒ I = Σ_(n=1) ^∞ (((−1)^(n−1) )/(n(n+2))) =(1/2)Σ_(n=1) ^∞ (−1)^(n−1) {(1/n) −(1/(n+2))} =(1/2) Σ_(n=1) ^∞ (((−1)^(n−1) )/n) −(1/2)Σ_(n=1) ^∞ (((−1)^(n−1) )/(n+2)) but Σ_(n=1) ^∞ (((−1)^(n−1) )/n) =ln(2) Σ_(n=1) ^∞ (((−1)^(n−1) )/(n+2)) =Σ_(n=3) ^∞ (((−1)^(n−3) )/n) =Σ_(n=3) ^∞ (((−1)^(n−1) )/n) =ln(2)−{1 −(1/2)}=ln(2)−(1/2) ⇒ I =(1/2)ln(2)−(1/2){ln(2)−(1/2)} ⇒I =(1/4)
$$\left.\mathrm{3}\right){let}\:{I}\:=\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−\mathrm{2}{x}} {ln}\left(\mathrm{1}+{e}^{\left.−{x}\right)} {dx}\right. \\ $$$${I}\:=\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−\mathrm{2}{x}} \left(\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:{e}^{−{nx}} \right){dx} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:\int_{\mathrm{0}} ^{\infty} \:\:\:{e}^{−\left({n}+\mathrm{2}\right){x}} {dx}\:{but} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:{e}^{−\left({n}+\mathrm{2}\right){x}} {dx}=\left[\frac{−\mathrm{1}}{{n}+\mathrm{2}}\:{e}^{−\left({n}+\mathrm{2}\right){x}} \right]_{\mathrm{0}} ^{+\infty} =\frac{\mathrm{1}}{{n}+\mathrm{2}}\:\Rightarrow \\ $$$${I}\:=\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}\left({n}+\mathrm{2}\right)}\:=\frac{\mathrm{1}}{\mathrm{2}}\sum_{{n}=\mathrm{1}} ^{\infty} \left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left\{\frac{\mathrm{1}}{{n}}\:−\frac{\mathrm{1}}{{n}+\mathrm{2}}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:−\frac{\mathrm{1}}{\mathrm{2}}\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}+\mathrm{2}}\:{but} \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:={ln}\left(\mathrm{2}\right) \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}+\mathrm{2}}\:=\sum_{{n}=\mathrm{3}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{3}} }{{n}} \\ $$$$=\sum_{{n}=\mathrm{3}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:={ln}\left(\mathrm{2}\right)−\left\{\mathrm{1}\:−\frac{\mathrm{1}}{\mathrm{2}}\right\}={ln}\left(\mathrm{2}\right)−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\:{I}\:=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{2}\right)−\frac{\mathrm{1}}{\mathrm{2}}\left\{{ln}\left(\mathrm{2}\right)−\frac{\mathrm{1}}{\mathrm{2}}\right\}\:\Rightarrow{I}\:=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$ \\ $$$$ \\ $$
Commented by prof Abdo imad last updated on 05/Aug/18
let J = ∫_0 ^∞ e^(−x) ln(1+e^(−2x) )dx we have J = ∫_0 ^∞ e^(−x) (Σ_(n=1) ^∞ (((−1)^(n−1) )/n) e^(−2nx) )dx =Σ_(n=1) ^∞ (((−1)^(n−1) )/n) ∫_0 ^∞ e^(−(2n+1)x) dx =Σ_(n=1) ^∞ (((−1)^(n−1) )/n)[((−1)/(2n+1)) e^(−(2n+1)x) ]_0 ^(+∞) =Σ_(n=1) ^∞ (((−1)^(n−1) )/(n(2n+1))) ⇒ (1/2)J =Σ_(n=1) ^∞ (−1)^(n−1) { (1/(2n))−(1/(2n+1))} =(1/2)Σ_(n=1) ^∞ (((−1)^(n−1) )/n) +Σ_(n=1) ^∞ (((−1)^n )/(2n+1)) =((ln(2))/2) +(π/4) −1 ⇒J =ln(2)+(π/2) −2 .
$${let}\:\:{J}\:=\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{x}} {ln}\left(\mathrm{1}+{e}^{−\mathrm{2}{x}} \right){dx}\:{we}\:{have} \\ $$$${J}\:=\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−{x}} \left(\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:{e}^{−\mathrm{2}{nx}} \right){dx} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−\left(\mathrm{2}{n}+\mathrm{1}\right){x}} {dx} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\left[\frac{−\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\:{e}^{−\left(\mathrm{2}{n}+\mathrm{1}\right){x}} \right]_{\mathrm{0}} ^{+\infty} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}\left(\mathrm{2}{n}+\mathrm{1}\right)}\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{J}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left\{\:\frac{\mathrm{1}}{\mathrm{2}{n}}−\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:\:+\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{1}} \\ $$$$=\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}}\:+\frac{\pi}{\mathrm{4}}\:−\mathrm{1}\:\Rightarrow{J}\:={ln}\left(\mathrm{2}\right)+\frac{\pi}{\mathrm{2}}\:−\mathrm{2}\:. \\ $$$$ \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 05/Aug/18
f(a,b)=∫_0 ^∞ e^(−ax) ln(1+e^(−bx) )dx after intregation the results will be in terms of a and b so we can write df=((∂f/∂a))_b da +((∂f/∂b))_a db (df/da)=∫_0 ^∞ ln(1+e^(−bx) ).(∂/∂a)(e^(−ax) ) dx (df/da)=∫_0 ^∞ ln(1+e^(−bx) ).(−ae^(−ax) )dx (df/da)=−af (df/f)=−ada lnf=−(a^2 /2)+c_1 f(a,b) =∫_0 ^∞ ln(1+e^(−bx) )e^(−ax) dx (df/db)=∫_0 ^∞ e^(−ax) .(∂/∂b){ln(1+e^(−bx) ) dx (df/db)=∫_0 ^∞ e^(−ax) .((−be^(−bx) )/(1+e^(−bx) )) dx (df/db)=∫_0 ^∞ (−b)(e^(−ax−bx) /(e^(bx) +1)).(e^(bx) /)dx (df/db)=(−b)∫_0 ^∞ (e^(−ax) /(1+e^(bx) )) dx let t=1+e^(bx) dt=e^(bx) .b.dx dx=(dt/(b(t−1))) e^(bx) =t−1 e^x =(t−1)^(1/b) so e^(−ax) =(t−1)^((−a)/b) (df/db)=(−b)∫_2 ^∞ (((t−1)^((−a)/b) )/t)×(dt/(b(t−1))) (df/db)=(−1)∫_2 ^∞ (((t−1)^(((−a)/b)−1) )/t) contd...
$${f}\left({a},{b}\right)=\int_{\mathrm{0}} ^{\infty} {e}^{−{ax}} {ln}\left(\mathrm{1}+{e}^{−{bx}} \right){dx} \\ $$$${after}\:{intregation}\:{the}\:{results}\:{will}\:{be}\:{in}\:{terms}\:{of}\:{a}\:{and}\:{b} \\ $$$$\:{so}\:{we}\:{can}\:{write} \\ $$$$ \\ $$$${df}=\left(\frac{\partial{f}}{\partial{a}}\right)_{{b}} \:{da}\:+\left(\frac{\partial{f}}{\partial{b}}\right)_{{a}} {db} \\ $$$$\frac{{df}}{{da}}=\int_{\mathrm{0}} ^{\infty} {ln}\left(\mathrm{1}+{e}^{−{bx}} \right).\frac{\partial}{\partial{a}}\left({e}^{−{ax}} \right)\:{dx} \\ $$$$\frac{{df}}{{da}}=\int_{\mathrm{0}} ^{\infty} {ln}\left(\mathrm{1}+{e}^{−{bx}} \right).\left(−{ae}^{−{ax}} \right){dx} \\ $$$$\frac{{df}}{{da}}=−{af} \\ $$$$\frac{{df}}{{f}}=−{ada} \\ $$$${lnf}=−\frac{{a}^{\mathrm{2}} }{\mathrm{2}}+{c}_{\mathrm{1}} \\ $$$${f}\left({a},{b}\right)\:=\int_{\mathrm{0}} ^{\infty} \:{ln}\left(\mathrm{1}+{e}^{−{bx}} \right){e}^{−{ax}} {dx} \\ $$$$\frac{{df}}{{db}}=\int_{\mathrm{0}} ^{\infty} {e}^{−{ax}} .\frac{\partial}{\partial{b}}\left\{{ln}\left(\mathrm{1}+{e}^{−{bx}} \right)\:{dx}\right. \\ $$$$\frac{{df}}{{db}}=\int_{\mathrm{0}} ^{\infty} {e}^{−{ax}} .\frac{−{be}^{−{bx}} }{\mathrm{1}+{e}^{−{bx}} }\:{dx} \\ $$$$\frac{{df}}{{db}}=\int_{\mathrm{0}} ^{\infty} \left(−{b}\right)\frac{{e}^{−{ax}−{bx}} }{{e}^{{bx}} +\mathrm{1}}.\frac{{e}^{{bx}} }{}{dx} \\ $$$$\:\:\frac{{df}}{{db}}=\left(−{b}\right)\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{ax}} }{\mathrm{1}+{e}^{{bx}} }\:{dx} \\ $$$${let}\:{t}=\mathrm{1}+{e}^{{bx}} \:\:\:\:{dt}={e}^{{bx}} .{b}.{dx} \\ $$$$\:\:\:{dx}=\frac{{dt}}{{b}\left({t}−\mathrm{1}\right)}\:\: \\ $$$${e}^{{bx}} ={t}−\mathrm{1}\:\:\:{e}^{{x}} =\left({t}−\mathrm{1}\right)^{\frac{\mathrm{1}}{{b}}} \:\:\:\:{so}\:{e}^{−{ax}} =\left({t}−\mathrm{1}\right)^{\frac{−{a}}{{b}}} \\ $$$$\frac{{df}}{{db}}=\left(−{b}\right)\int_{\mathrm{2}} ^{\infty} \:\frac{\left({t}−\mathrm{1}\right)^{\frac{−{a}}{{b}}} }{{t}}×\frac{{dt}}{{b}\left({t}−\mathrm{1}\right)} \\ $$$$\frac{{df}}{{db}}=\left(−\mathrm{1}\right)\int_{\mathrm{2}} ^{\infty} \frac{\left({t}−\mathrm{1}\right)^{\frac{−{a}}{{b}}−\mathrm{1}} }{{t}} \\ $$$${contd}… \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *