Question Number 32365 by prof Abdo imad last updated on 23/Mar/18
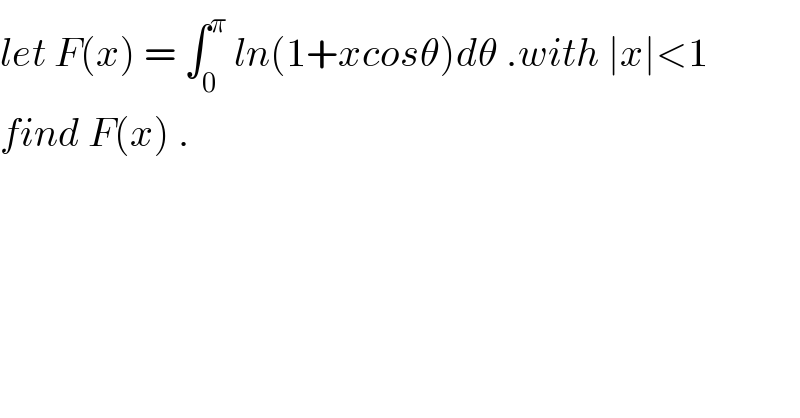
$${let}\:{F}\left({x}\right)\:=\:\int_{\mathrm{0}} ^{\pi} \:{ln}\left(\mathrm{1}+{xcos}\theta\right){d}\theta\:.{with}\:\mid{x}\mid<\mathrm{1} \\ $$$${find}\:{F}\left({x}\right)\:. \\ $$
Commented by prof Abdo imad last updated on 25/Mar/18
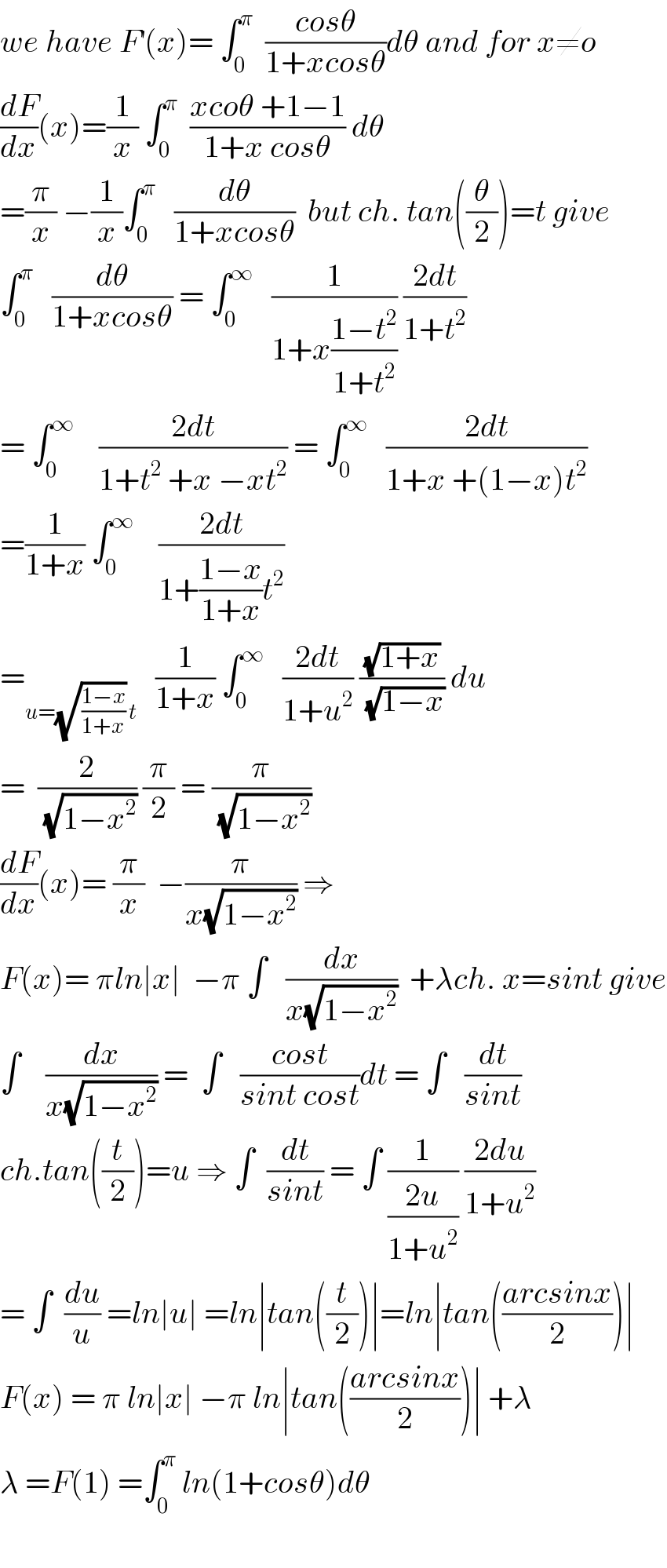
$${we}\:{have}\:{F}^{'} \left({x}\right)=\:\int_{\mathrm{0}} ^{\pi} \:\:\frac{{cos}\theta}{\mathrm{1}+{xcos}\theta}{d}\theta\:{and}\:{for}\:{x}\neq{o} \\ $$$$\frac{{dF}}{{dx}}\left({x}\right)=\frac{\mathrm{1}}{{x}}\:\int_{\mathrm{0}} ^{\pi} \:\:\frac{{xco}\theta\:+\mathrm{1}−\mathrm{1}}{\mathrm{1}+{x}\:{cos}\theta}\:{d}\theta \\ $$$$=\frac{\pi}{{x}}\:−\frac{\mathrm{1}}{{x}}\int_{\mathrm{0}} ^{\pi} \:\:\:\frac{{d}\theta}{\mathrm{1}+{xcos}\theta}\:\:{but}\:{ch}.\:{tan}\left(\frac{\theta}{\mathrm{2}}\right)={t}\:{give} \\ $$$$\int_{\mathrm{0}} ^{\pi} \:\:\:\frac{{d}\theta}{\mathrm{1}+{xcos}\theta}\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{1}}{\mathrm{1}+{x}\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} \:+{x}\:−{xt}^{\mathrm{2}} }\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{x}\:+\left(\mathrm{1}−{x}\right){t}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}+{x}}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{\mathrm{2}{dt}}{\mathrm{1}+\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}{t}^{\mathrm{2}} } \\ $$$$=_{{u}=\sqrt{\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}}\:{t}} \:\:\:\frac{\mathrm{1}}{\mathrm{1}+{x}}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{u}^{\mathrm{2}} }\:\frac{\sqrt{\mathrm{1}+{x}}}{\:\sqrt{\mathrm{1}−{x}}}\:{du} \\ $$$$=\:\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:\frac{\pi}{\mathrm{2}}\:=\:\frac{\pi}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$$$\frac{{dF}}{{dx}}\left({x}\right)=\:\frac{\pi}{{x}}\:\:−\frac{\pi}{{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:\Rightarrow \\ $$$${F}\left({x}\right)=\:\pi{ln}\mid{x}\mid\:\:−\pi\:\int\:\:\:\frac{{dx}}{{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:\:+\lambda{ch}.\:{x}={sint}\:{give} \\ $$$$\int\:\:\:\:\frac{{dx}}{{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:=\:\:\int\:\:\:\frac{{cost}}{{sint}\:{cost}}{dt}\:=\:\int\:\:\:\frac{{dt}}{{sint}} \\ $$$${ch}.{tan}\left(\frac{{t}}{\mathrm{2}}\right)={u}\:\Rightarrow\:\int\:\:\frac{{dt}}{{sint}}\:=\:\int\:\frac{\mathrm{1}}{\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }}\:\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$$=\:\int\:\:\frac{{du}}{{u}}\:={ln}\mid{u}\mid\:={ln}\mid{tan}\left(\frac{{t}}{\mathrm{2}}\right)\mid={ln}\mid{tan}\left(\frac{{arcsinx}}{\mathrm{2}}\right)\mid \\ $$$${F}\left({x}\right)\:=\:\pi\:{ln}\mid{x}\mid\:−\pi\:{ln}\mid{tan}\left(\frac{{arcsinx}}{\mathrm{2}}\right)\mid\:+\lambda \\ $$$$\lambda\:={F}\left(\mathrm{1}\right)\:=\int_{\mathrm{0}} ^{\pi} \:{ln}\left(\mathrm{1}+{cos}\theta\right){d}\theta \\ $$$$ \\ $$
Commented by prof Abdo imad last updated on 25/Mar/18
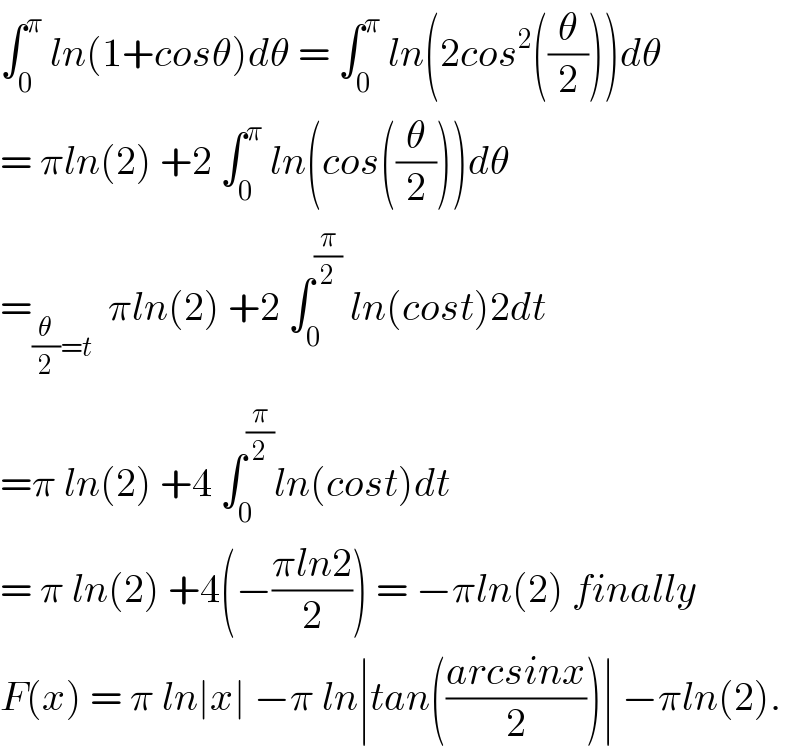
$$\int_{\mathrm{0}} ^{\pi} \:{ln}\left(\mathrm{1}+{cos}\theta\right){d}\theta\:=\:\int_{\mathrm{0}} ^{\pi} \:{ln}\left(\mathrm{2}{cos}^{\mathrm{2}} \left(\frac{\theta}{\mathrm{2}}\right)\right){d}\theta \\ $$$$=\:\pi{ln}\left(\mathrm{2}\right)\:+\mathrm{2}\:\int_{\mathrm{0}} ^{\pi} \:{ln}\left({cos}\left(\frac{\theta}{\mathrm{2}}\right)\right){d}\theta \\ $$$$=_{\frac{\theta}{\mathrm{2}}={t}} \:\:\pi{ln}\left(\mathrm{2}\right)\:+\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{ln}\left({cost}\right)\mathrm{2}{dt} \\ $$$$=\pi\:{ln}\left(\mathrm{2}\right)\:+\mathrm{4}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({cost}\right){dt} \\ $$$$=\:\pi\:{ln}\left(\mathrm{2}\right)\:+\mathrm{4}\left(−\frac{\pi{ln}\mathrm{2}}{\mathrm{2}}\right)\:=\:−\pi{ln}\left(\mathrm{2}\right)\:{finally} \\ $$$${F}\left({x}\right)\:=\:\pi\:{ln}\mid{x}\mid\:−\pi\:{ln}\mid{tan}\left(\frac{{arcsinx}}{\mathrm{2}}\right)\mid\:−\pi{ln}\left(\mathrm{2}\right). \\ $$
Commented by prof Abdo imad last updated on 25/Mar/18

$${F}\left(\mathrm{0}\right)\:=\mathrm{0} \\ $$
